P1578 奶牛浴场
题目描述
由于John建造了牛场围栏,激起了奶牛的愤怒,奶牛的产奶量急剧减少。为了讨好奶牛,John决定在牛场中建造一个大型浴场。但是John的奶牛有一个奇怪的习惯,每头奶牛都必须在牛场中的一个固定的位置产奶,而奶牛显然不能在浴场中产奶,于是,John希望所建造的浴场不覆盖这些产奶点。这回,他又要求助于Clevow了。你还能帮助Clevow吗?
John的牛场和规划的浴场都是矩形。浴场要完全位于牛场之内,并且浴场的轮廓要与牛场的轮廓平行或者重合。浴场不能覆盖任何产奶点,但是产奶点可以位于浴场的轮廓上。
Clevow当然希望浴场的面积尽可能大了,所以你的任务就是帮她计算浴场的最大面积。
输入输出格式
输入格式:
输入文件的第一行包含两个整数L和W,分别表示牛场的长和宽。文件的第二行包含一个整数n,表示产奶点的数量。以下n行每行包含两个整数x和y,表示一个产奶点的坐标。所有产奶点都位于牛场内,即:0<=x<=L,0<=y<=W。
输出格式:
输出文件仅一行,包含一个整数S,表示浴场的最大面积。
输入输出样例
说明
0<=n<=5000
1<=L,W<=30000
Winter Camp 2002
洛谷题解:
这个题目很出名,可以在百度搜索王知昆国家队dalao的论文,其中说的非常详细,但是可惜的是在他本人的代码中也有两个bug,我上面的两组数据他的代码也出现的错误。可能是由于本题数据较水,所以很多有bug的代码水过去了。
我来简单的说一下:
先枚举极大子矩形的左边界,然后从左到右依次扫描每一个障碍点,并不断修改可行的上下边界,从而枚举出所有以这个定点为左边界的极大子矩形。考虑如图2中的三个点,现在我们要确定所有以1号点为左边界的极大矩形。先将1号点右边的点按横坐标排序。然后按从左到右的顺序依次扫描1号点右边的点,同时记录下当前的可行的上下边界。

开始时令当前的上下边界分别为整个矩形的上下边界。然后开始扫描。第一次遇到2号点,以2号点作为右边界,结合当前的上下边界,就得到一个极大子矩形(如图3)。

同时,由于所求矩形不能包含2号点,且2号点在1号点的下方,所以需要修改当前的下边界,即以2号点的纵坐标作为新的下边界。第二次遇到3号点,这时以3号点的横坐标作为右边界又可以得到一个满足性质1的矩形(如图4)。

类似的,需要相应地修改上边界。以此类推,如果这个点是在当前点(确定左边界的点)上方,则修改上边界;如果在下方,则修改下边界;如果处在同一行,则可中止搜索(因为后面的矩形面积都是0了)。由于已经在障碍点集合中增加了整个矩形右上角和右下角的两个点,所以不会遗漏右边界与整个矩形的右边重合的极大子矩形(如图5)。
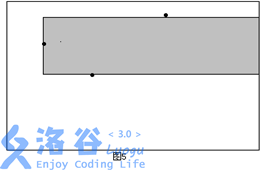
需要注意的是,如果扫描到的点不在当前的上下边界内,那么就不需要对这个点进行处理。
这样做是否将所有的极大子矩形都枚举过了呢?
可以发现,这样做只考虑到了左边界覆盖一个点的矩形,因此我们还需要枚举左边界与整个矩形的左边界重合的情况。这还可以分为两类情况。一种是左边界与整个举行的左边界重合,而右边界覆盖了一个障碍点的情况,对于这种情况,可以用类似的方法从右到左扫描每一个点作为右边界的情况。这就是上面第一个数据楼下二位错在哪里。
另一种是左右边界均与整个矩形的左右边界重合的情况,对于这类情况我们可以在预处理中完成:先将所有点按纵坐标排序,然后可以得到以相邻两个点的纵坐标为上下边界,左右边界与整个矩形的左右边界重合的矩形,显然这样的矩形也是极大子矩形,因此也需要被枚举到。这就是上面第二个数据楼下两位错在哪里。
对于开始预处理,需要人为添加0,0;0,l;w,0;l,w四个点,这时王知昆dalao错的第一个地方。
对于他其中的一个剪枝优化显然是不小心打错了。具体会在代码中说。
参考代码:
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #define re register 5 #define REP(i,a,b) for (re int i=(a);i<=(b);i++) 6 #define DREP(i,a,b) for (re int i=(a);i>=(b);i--) 7 using namespace std; 8 const int N=5e3+7; 9 struct Cow{ 10 int x,y; 11 inline bool operator < (const Cow &rhs) const { 12 if (x!=rhs.x)return x<rhs.x; 13 return y<rhs.y; 14 } 15 }a[N]; 16 int L,W,n; 17 inline bool cmp(Cow a,Cow b){ 18 return a.y<b.y; 19 } 20 inline int read(){ 21 re int x=0,f=1;char ch=getchar(); 22 while (ch<'0' || ch>'9'){if (ch=='-')f=-1;ch=getchar();} 23 while ('0'<=ch && ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();} 24 return x*f; 25 } 26 int main(){ 27 L=read(),W=read(),n=read(); 28 REP(i,1,n)a[i].x=read(),a[i].y=read(); 29 a[++n].x=0;a[n].y=0; 30 a[++n].x=L;a[n].y=0; 31 a[++n].x=0;a[n].y=W; 32 a[++n].x=L;a[n].y=W; 33 sort(a+1,a+n+1); 34 int res=0; 35 REP(i,1,n){ 36 re int h=W,l=0,v=L-a[i].x; 37 REP(j,i+1,n)if (a[j].y<=h && a[j].y>=l){ 38 if (v*(h-l)<=res)break; 39 res=max(res,(a[j].x-a[i].x)*(h-l)); 40 if (a[j].y==a[i].y)break; 41 if (a[j].y>a[i].y)h=min(h,a[j].y); 42 else l=max(l,a[j].y); 43 } 44 h=W,l=0,v=a[i].x;//王知昆dalao在此处仍将v设为l-a[i].x,这显然不对,可以自己想一想。 45 DREP(j,i-1,1) 46 if (a[j].y<=h && a[j].y>=l){ 47 if (v*(h-l)<=res)break; 48 res=max(res,(a[i].x-a[j].x)*(h-l)); 49 if (a[i].y==a[j].y)break; 50 if (a[j].y>a[i].y)h=min(h,a[j].y); 51 else l=max(l,a[j].y); 52 } 53 } 54 sort(a+1,a+n+1,cmp); 55 REP(i,1,n-1)res=max(res,(a[i+1].y-a[i].y)*L); 56 printf("%d",res); 57 return 0; 58 }