P1198 [JSOI2008]最大数(线段树)
题目描述
现在请求你维护一个数列,要求提供以下两种操作:
1、 查询操作。
语法:Q L
功能:查询当前数列中末尾L个数中的最大的数,并输出这个数的值。
限制:L不超过当前数列的长度。(L>=0)
2、 插入操作。
语法:A n
功能:将n加上t,其中t是最近一次查询操作的答案(如果还未执行过查询操作,则t=0),并将所得结果对一个固定的常数D取模,将所得答案插入到数列的末尾。
限制:n是整数(可能为负数)并且在长整范围内。
注意:初始时数列是空的,没有一个数。
输入输出格式
输入格式:
第一行两个整数,M和D,其中M表示操作的个数(M <= 200,000),D如上文中所述,满足(0<D<2,000,000,000)
接下来的M行,每行一个字符串,描述一个具体的操作。语法如上文所述。
输出格式:
对于每一个查询操作,你应该按照顺序依次输出结果,每个结果占一行。
输入输出样例
说明
[JSOI2008]
本题数据已加强
分析解答:
这个题目线段树,树状数组,单调栈,分块等方法都可以做;
核心是查找一串数中的最大值。
下面是线段树的解法:
这道题并不需要提前建树,只要按照输入的顺序挨个添加就好啦
要是不会线段树的话,可以先去看一下线段树模板1
运用线段树的算法。首先建树,把所有的节点的值赋成min_int。用[i,j]表示该区间的最大值。
1)读入Q L操作。用len表示区间的大小,在len+1的位置放入(L+T)%D的值。
2)读入A n操作。输出区间[len-n+1,len]这个区间中的最大值,并把t的值进行更新。
得分:100
时间复杂度:O(nlogn)
空间复杂度:O(4*n)
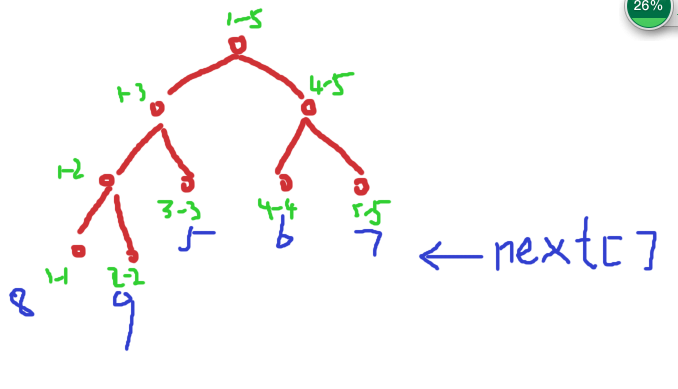

next数组把所有叶子节点的位置都找到了
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 struct tree 6 { 7 int l,r,_max;//左右边界和最大值 8 }a[800000];//4倍空间 9 int n,m,d,x,t,next[200001]; 10 //建树 11 void make_tree(int x,int l,int r) 12 { 13 a[x].l=l; 14 a[x].r=r; 15 //叶子节点 16 if(l==r) 17 { 18 //这里x是root 19 //next里面记录的是所有叶子节点的位置,或者说编号 20 next[l]=x; 21 return; 22 //这里本来是要做数据的初始化的,但是因为现在数据还没加进来,做不了 23 } 24 int mid=(l+r)/2; 25 //左右子树 26 make_tree(x*2,l,mid); 27 make_tree(x*2+1,mid+1,r); 28 } 29 void add(int x) 30 { 31 a[next[++n]]._max=(x+t)%d;//这一步就是做叶子节点数据的初始化 32 //本来n是0,第一个数是8的位置,那就插到8的位置就好 33 int temp=next[n]; 34 //节点发生改变,肯定要更新父亲节点 35 //比如说第一个节点的位置是8,那么temp就是从8 4 2 1,这样一直更新到root节点 36 while(a[temp]._max>a[temp/2]._max)//子节点大于父亲节点才更新 37 { 38 //无论是左右孩子,除2都可以得到父亲 39 a[temp/2]._max=a[temp]._max; 40 temp=temp/2; 41 } 42 } 43 //查询操作 ,这里的x是根节点 ,y是左边界 ,y是我们要查询的边界的左边界 44 int q(int x,int y) 45 { 46 //包含的情况,因为求最后几个,右边界是固定的 47 if(a[x].l>=y) return a[x]._max; 48 //没有相交的情况 49 if(a[x].r<y) return 0; 50 //相交又不包含的情况 51 //左右孩子中的大值 52 return max(q(x*2,y),q(x*2+1,y)); 53 } 54 void print(int m){ 55 cout<<"i"<<" "<<"next[i]"<<" "<<endl; 56 for(int i=1;i<=2*m;i++){ 57 cout<<i<<" "<<next[i]<<" "<<endl; 58 } 59 } 60 int main() 61 { 62 // freopen("in.txt","r",stdin); 63 cin>>m>>d; 64 a[1].l=1; 65 a[1].r=m; 66 //这里就是左+右除2 67 make_tree(2,1,(m+1)/2); 68 make_tree(3,(m+1)/2+1,m); 69 // print(m); 70 for(int i=1;i<=m;i++) 71 { 72 char ch; 73 cin>>ch; 74 cin>>x; 75 //插入操作 76 if(ch=='A') add(x); 77 if(ch=='Q') 78 { 79 //查询操作,比如x是2,比如5个操作,因为进行了两次插入操作,所以n就是2,q(1,2-2+1) 80 //这里的1是root,而n-x+1是我们要查询的左边界,因为右边界不用管 81 t=q(1,n-x+1); 82 cout<<t<<endl; 83 } 84 } 85 // print(m); 86 }