DFS序

DFS序

总结：

1、树转化为线性：将树通过dfs转化为线性结构，这就是dfs序，和树链剖分有点相似

2、普通树转化为线段树：记录每个节点构成的树（子树）的起点和终点，起点是自己，这样每个点就构成了一个区间，然后对区间的操作就和线段树和树状数组一样了。

3、DFS序主要用来做子树的更新，因为DFS序中子树都是连续的。时间复杂度看树的储存结构，O（1）。

4、树的储存可以用图来存储，图的数组模拟邻接矩阵：小兵应该先武装好自己，然后再加入队伍，队长负责周转（管最前面一个）。

 

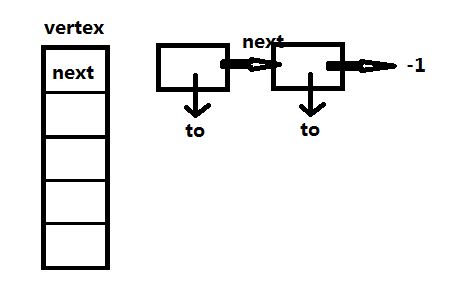
详解：

给定一棵n个节点的树，m次查询，每次查询需要求出某个节点深度为h的所有子节点。

对于这个问题如果试图去对每个节点保存所有深度的子节点，在数据大的时候内存会吃不消；或者每次查询的时候去遍历一遍，当数据大的时候，时间效率会非常低。

此时如果使用dfs序维护树结构就可以轻松地解决这个问题。

作为预处理，首先将将树的所有节点按深度保存起来，每个深度的所有节点用一个线性结构保存，每个深度的节点相对顺序要和前序遍历一致。

然后从树的根节点进行dfs，对于每个节点记录两个信息，一个是dfs进入该节点的时间戳in[id]，另一个是dfs离开该节点的时间戳out[id]。

最后对于每次查询，求节点v在深度h的所有子节点，只需将深度为h并且dfs进入时间戳在in[v]和out[v]之间的所有节点都求出来即可，由于对于每个深度的所有节点，相对顺序和前序遍历的顺序以致，那么他们的dfs进入时间戳也是递增的，于是可以通过二分搜索求解。

分析

Step 1：

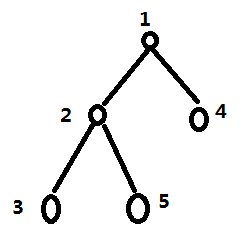
如下图，可以看到，由于普通的树并不具有区间的性质，所以在考虑使用线段树作为解题思路时，需要对给给定的数据进行转化，首先对这棵树进行一次dfs遍历，记录dfs序下每个点访问起始时间与结束时间，记录起始时间是前序遍历，结束时间是后序遍历，同时对这课树进行重标号。

Step 2：

         如下图，DFS之后，那么树的每个节点就具有了区间的性质。

         那么此时，每个节点对应了一个区间，而且可以看到，每个节点对应的区间正好“管辖”了它子树所有节点的区间，那么对点或子树的操作就转化为了对区间的操作。

【PS: 如果对树的遍历看不懂的话，不妨待会对照代码一步一步调试，或者在纸上模拟过程~】

Step 3：

         这个时候，每次对节点进行更新或者查询，就是线段树和树状数组最基本的实现了…

树是一种非线性结构，一般而言，我们总是想办法将其转化为线性结构，将树上操作包括子树操作、路径操作等转化为数组上的区间操作，从而在一个较为理想的复杂度内加以解决。将树“拍平”的方法有很多，例如欧拉序、HLD等。实际上欧拉序也是在DFS过程中得到的。不过通常而言，我们所说的DFS序是指：每个节点进出栈的时间序列。

 
考虑上图中树的DFS序，应为 

其中，每个节点均会出现2次，第一次是进入DFS的时刻，第二次是离开DFS的时刻。分别称之为In与Out。在区间操作中，如果某个节点出现了2次，则该节点将被“抵消”。所以通常会将Out时刻对应的点设置为负数。

树的DFS序列有几个有用的性质：

1. 任意子树是连续的。例如子树BEFK，在序列中对应BEEFKKFB；子树CGHI，在序列中对应连续区间CGGHHIIC。
2. 任意点对(a,b)之间的路径，可分为2种情况，首先令lca是a、b的最近公共祖先： 
   
   1. 若lca是a、b之一，则a、b之间的In时刻的区间或者Out时刻区间就是其路径。例如AK之间的路径就对应区间ABEEFK，或者KFBCGGHHIICA。
   2. 若lca另有其人，则a、b之间的路径为In[a]、Out[b]之间的区间或者In[b]、Out[a]之间的区间。另外，还需额外加上lca！！！考虑EK路径，对应为EFK再加上B。考虑EH之间的路径，对应为EFKKFBCGGH再加上A。

利用这些性质，可以利用DFS序列完成子树操作和路径操作，同时也有可能将莫队算法应用到树上从而得到树上莫队。

代码：

dfs序是处理树上问题很重要的一个武器，主要能够解决对于一个点，它的子树上的一些信息的维护。 
就比如那天百度之星round1A的1003题，就是dfs序+线段树维护每个点到0点的距离，然后对于每个点的更新，只需要更新它和它的子树上的点到0点的距离，查询的话就是它的子树上的最大值即可 
我的dfs序开的空间就是n，因为只在入的地方时间戳++，出来的地方时间戳不变，线段树的每个节点应该是时间戳

void dfs(int u,int fa){
    p1[u]=++ti;
    dfsnum[ti]=u;
    for(int i=head[u];i!=-1;i=edge[i].next){
        int v=edge[i].v;
        if(v==fa) continue;
        dfs(v,u);
    }
    p2[u]=ti;//时间戳不变，空间为O(n)
}

例题：

BZOJ4034需要在树上完成3类操作，单点更新，子树更新，以及根到指定节点的路径查询。利用性质1以及性质2.1即可完成，连LCA都无需求出。对整个DFS序列使用线段树进行维护，注意到整个序列实际上有正有负，因此额外用一个域来表示正数的个数。

4034: [HAOI2015]树上操作

Time Limit: 10 Sec  Memory Limit: 256 MB
Submit: 6323  Solved: 2094
[Submit][Status][Discuss]

Description

有一棵点数为 N 的树，以点 1 为根，且树点有边权。然后有 M 个

操作，分为三种：

操作 1 ：把某个节点 x 的点权增加 a 。

操作 2 ：把某个节点 x 为根的子树中所有点的点权都增加 a 。

操作 3 ：询问某个节点 x 到根的路径中所有点的点权和。

Input

第一行包含两个整数 N, M 。表示点数和操作数。接下来一行 N 个整数，表示树中节点的初始权值。接下来 N-1 

行每行三个正整数 fr, to ， 表示该树中存在一条边 (fr, to) 。再接下来 M 行，每行分别表示一次操作。其中

第一个数表示该操作的种类（ 1-3 ） ，之后接这个操作的参数（ x 或者 x a ） 。

 

Output

对于每个询问操作，输出该询问的答案。答案之间用换行隔开。

 

Sample Input

5 5
1 2 3 4 5
1 2
1 4
2 3
2 5
3 3
1 2 1
3 5
2 1 2
3 3

Sample Output

6
9
13

HINT

 对于 100% 的数据， N,M<=100000 ，且所有输入数据的绝对值都不会超过 10^6 。

Source

鸣谢bhiaibogf提供

#include <cstdio>
#include <climits>
#include <algorithm>
#include <iostream>
using namespace std;

int const SIZE = 100100;
typedef long long weight_t;

struct edge_t{//边 
    int to;
    int next;
}Edge[SIZE<<1];//双向的  所以*2 
int Vertex[SIZE];
int ECnt;
weight_t W[SIZE];

//数组模拟邻接矩阵：顶点记录的是下一个点，顶点负责转运 
inline void mkEdge(int a,int b){//造a-b这条边 
    //先把节点的信息补充好，再建立联系
    //先武装好自己，然后再图报效
    //每个队的长官记录每个队节点的分配信息 
    Edge[ECnt].to = b;
    Edge[ECnt].next = Vertex[a];
    Vertex[a] = ECnt++;

    Edge[ECnt].to = a;
    Edge[ECnt].next = Vertex[b];
    Vertex[b] = ECnt++;
}

int InIdx[SIZE],OutIdx[SIZE];
int InOut[SIZE<<1];
int NewIdx[SIZE<<1];
int NCnt;

void dfs(int node,int parent){
    NewIdx[NCnt] = node;
    InOut[NCnt] = 1;
    InIdx[node] = NCnt++;
    for(int next=Vertex[node];next;next=Edge[next].next){
        int son = Edge[next].to;
        if ( son != parent ) dfs(son,node);
    }
    NewIdx[NCnt] = node;
    InOut[NCnt] = -1;
    OutIdx[node] = NCnt++;
}

int N;
weight_t StSum[SIZE<<3];
weight_t Lazy[SIZE<<3];
int Flag[SIZE<<3];//The count of the positive number in the range

inline int lson(int x){return x<<1;}
inline int rson(int x){return lson(x)|1;}

inline void _pushUp(int t){
    StSum[t] = StSum[lson(t)] + StSum[rson(t)];
    Flag[t] = Flag[lson(t)] + Flag[rson(t)];
}

inline void _pushDown(int t){
    if ( 0LL == Lazy[t] ) return;

    weight_t& x = Lazy[t];

    int son = lson(t);
    StSum[son] += Flag[son] * x;
    Lazy[son] += x;

    son = rson(t);
    StSum[son] += Flag[son] * x;
    Lazy[son] += x;

    x = 0LL;
}

void build(int t,int s,int e){
    Lazy[t] = 0LL;
    if ( s == e ){
        StSum[t] = InOut[s] * W[NewIdx[s]];
        Flag[t] = InOut[s];
        return;
    }

    int m = ( s + e ) >> 1;
    build(lson(t),s,m);
    build(rson(t),m+1,e);
    _pushUp(t);
}

void modify(int t,int s,int e,int a,int b,weight_t delta){
    if ( a <= s && e <= b ){
        StSum[t] += Flag[t] * delta;
        Lazy[t] += delta;
        return;
    }

    _pushDown(t);
    int m = ( s + e ) >> 1;
    if ( a <= m ) modify(lson(t),s,m,a,b,delta);
    if ( m < b ) modify(rson(t),m+1,e,a,b,delta);
    _pushUp(t);
}

weight_t query(int t,int s,int e,int a,int b){
    if ( a <= s && e <= b ){
        return StSum[t];
    }

    _pushDown(t);

    weight_t ret = 0LL;
    int m = ( s + e ) >> 1;
    if ( a <= m ) ret += query(lson(t),s,m,a,b);
    if ( m < b ) ret += query(rson(t),m+1,e,a,b);
    return ret;
}

inline weight_t query(int x){
    return query(1,1,N<<1,1,InIdx[x]);
}

inline void modify(int x,weight_t delta){
    modify(1,1,N<<1,InIdx[x],InIdx[x],delta);
    modify(1,1,N<<1,OutIdx[x],OutIdx[x],delta);
}

inline void modifySubtree(int x,weight_t delta){
    modify(1,1,N<<1,InIdx[x],OutIdx[x],delta);
}

//这里树的储存方式用的是图里面的数组仿邻接矩阵 
inline void initTree(int n){
    ECnt = NCnt = 1;
    //vertex是顶点，这就是存储边的方式 
    fill(Vertex,Vertex+n+1,0);
}

int M;
bool read(){
    if ( EOF == scanf("%d%d",&N,&M) ) return false;

    initTree(N);
    for(int i=1;i<=N;++i)scanf("%lld",W+i);//读权值 

    int a,b;
    for(int i=1;i<N;++i){
        scanf("%d%d",&a,&b);//读每一条边 
        mkEdge(a,b);//造边 
    }
    cout<<"Edge[i].to"<<" "<<"Edge[i].next"<<endl;
    for(int i=0;i<=20;i++){
        cout<<Edge[i].to<<" "<<Edge[i].next<<endl;
    } 
    dfs(1,0);
    build(1,1,N<<1);
    return true;
}

void proc(){
    int cmd,x;
    weight_t a;
    while(M--){
        scanf("%d%d",&cmd,&x);
        switch(cmd){
        case 1:scanf("%lld",&a);modify(x,a);break;
        case 2:scanf("%lld",&a);modifySubtree(x,a);break;
        case 3:printf("%lld
",query(x));break;
        }
    }
}
int main(){
    freopen("in.txt","r",stdin);
    while( read() ) proc();
    return 0;
}

HDU 3887 
题目传送门：http://acm.hdu.edu.cn/showproblem.php?pid=3887 
问你对于每个节点，它的子树上标号比它小的点有多少个 
子树的问题，dfs序可以很轻松的解决，因为点在它的子树上，所以在线段树中，必定在它的两个时间戳的区间之间，所以我们只需要从小到大考虑，它的区间里有多少个点已经放了，然后再把它放进去。很容易的解决了 
代码：

#include <map>
#include <set>
#include <stack>
#include <queue>
#include <cmath>
#include <string>
#include <vector>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <sstream>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#pragma comment(linker, "/STACK:102400000,102400000")

using namespace std;
#define   MAX           500005
#define   MAXN          6005
#define   maxnode       15
#define   sigma_size    30
#define   lson          l,m,rt<<1
#define   rson          m+1,r,rt<<1|1
#define   lrt           rt<<1
#define   rrt           rt<<1|1
#define   middle        int m=(r+l)>>1
#define   LL            long long
#define   ull           unsigned long long
#define   mem(x,v)      memset(x,v,sizeof(x))
#define   lowbit(x)     (x&-x)
#define   pii           pair<int,int>
#define   bits(a)       __builtin_popcount(a)
#define   mk            make_pair
#define   limit         10000

//const int    prime = 999983;
const int    INF   = 0x3f3f3f3f;
const LL     INFF  = 0x3f3f;
const double pi    = acos(-1.0);
//const double inf   = 1e18;
const double eps   = 1e-8;
const LL    mod    = 1e9+7;
const ull    mx    = 133333331;

/*****************************************************/
inline void RI(int &x) {
      char c;
      while((c=getchar())<'0' || c>'9');
      x=c-'0';
      while((c=getchar())>='0' && c<='9') x=(x<<3)+(x<<1)+c-'0';
 }
/*****************************************************/

struct Edge{
    int v,next;
}edge[MAX*2];
int head[MAX];
int tot;
int p1[MAX];
int p2[MAX];
int ti;
int sum[MAX<<2];

void init(){
    mem(head,-1);
    tot=0;ti=0;
}

void add_edge(int a,int b){
    edge[tot]=(Edge){b,head[a]};
    head[a]=tot++;
}

void dfs(int u,int fa){
    p1[u]=++ti;
    for(int i=head[u];i!=-1;i=edge[i].next){
        int v=edge[i].v;
        if(v==fa) continue;
        dfs(v,u);
    }
    p2[u]=ti;
}

void build(int l,int r,int rt){
    sum[rt]=0;
    if(l==r) return;
    middle;
    build(lson);
    build(rson);
}

void pushup(int rt){
    sum[rt]=sum[lrt]+sum[rrt];
}

void update(int l,int r,int rt,int pos,int d){
    if(l==r){
        sum[rt]+=d;
        return;
    }
    middle;
    if(pos<=m) update(lson,pos,d);
    else update(rson,pos,d);
    pushup(rt);
}

int query(int l,int r,int rt,int L,int R){
    if(L<=l&&r<=R) return sum[rt];
    middle;
    int ret=0;
    if(L<=m) ret+=query(lson,L,R);
    if(R>m) ret+=query(rson,L,R);
    return ret;
}

int main(){
    int n,p;
    while(cin>>n>>p&&n){
        init();
        for(int i=1;i<n;i++){
            int a,b;
            scanf("%d%d",&a,&b);
            add_edge(a,b);
            add_edge(b,a);
        }
        dfs(p,-1);
        build(1,n,1);
        for(int i=1;i<=n;i++){
            printf("%d",query(1,n,1,p1[i],p2[i]));
            if(i==n) printf("
");
            else printf(" ");
            update(1,n,1,p1[i],1);
        }
    }
    return 0;
}

poj 3321 
题目传送门：http://poj.org/problem?id=3321 
这题是一开始告诉你树上每个节点都有1个苹果，然后你对一个节点操作，如果有苹果，就拿走，没苹果，就放上，然后询问你以x为根的子树上有多少个苹果。 
dfs序水题，代码：

#include <map>
#include <set>
#include <stack>
#include <queue>
#include <cmath>
#include <string>
#include <vector>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <sstream>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#pragma comment(linker, "/STACK:102400000,102400000")

using namespace std;
#define   MAX           500005
#define   MAXN          6005
#define   maxnode       15
#define   sigma_size    30
#define   lson          l,m,rt<<1
#define   rson          m+1,r,rt<<1|1
#define   lrt           rt<<1
#define   rrt           rt<<1|1
#define   middle        int m=(r+l)>>1
#define   LL            long long
#define   ull           unsigned long long
#define   mem(x,v)      memset(x,v,sizeof(x))
#define   lowbit(x)     (x&-x)
#define   pii           pair<int,int>
#define   bits(a)       __builtin_popcount(a)
#define   mk            make_pair
#define   limit         10000

//const int    prime = 999983;
const int    INF   = 0x3f3f3f3f;
const LL     INFF  = 0x3f3f;
const double pi    = acos(-1.0);
//const double inf   = 1e18;
const double eps   = 1e-8;
const LL    mod    = 1e9+7;
const ull    mx    = 133333331;

/*****************************************************/
inline void RI(int &x) {
      char c;
      while((c=getchar())<'0' || c>'9');
      x=c-'0';
      while((c=getchar())>='0' && c<='9') x=(x<<3)+(x<<1)+c-'0';
 }
/*****************************************************/

struct Edge{
    int v,next;
}edge[MAX*2];
int head[MAX];
int tot;
int p1[MAX];
int p2[MAX];
int ti;
int sum[MAX<<2];

void init(){
    mem(head,-1);
    tot=0;ti=0;
}

void add_edge(int a,int b){
    edge[tot]=(Edge){b,head[a]};
    head[a]=tot++;
}

void dfs(int u,int fa){
    p1[u]=++ti;
    for(int i=head[u];i!=-1;i=edge[i].next){
        int v=edge[i].v;
        if(v==fa) continue;
        dfs(v,u);
    }
    p2[u]=ti;
}

void pushup(int rt){
    sum[rt]=sum[lrt]+sum[rrt];
}

void build(int l,int r,int rt){
    if(l==r){
        sum[rt]=1;
        return;
    }
    middle;
    build(lson);
    build(rson);
    pushup(rt);
}

void update(int l,int r,int rt,int pos){
    if(l==r){
        sum[rt]=sum[rt]^1;
        return;
    }
    middle;
    if(pos<=m) update(lson,pos);
    else update(rson,pos);
    pushup(rt);
}

int query(int l,int r,int rt,int L,int R){
    if(L<=l&&r<=R) return sum[rt];
    middle;
    int ret=0;
    if(L<=m) ret+=query(lson,L,R);
    if(R>m) ret+=query(rson,L,R);
    return ret;
}

int main(){
    int n;
    cin>>n;
    init();
    for(int i=1;i<n;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        add_edge(a,b);
        add_edge(b,a);
    }
    dfs(1,-1);
    build(1,n,1);
    int m;
    scanf("%d",&m);
    while(m--){
        char op;
        int a;
        getchar();
        scanf("%c%d",&op,&a);
        if(op=='Q') printf("%d
",query(1,n,1,p1[a],p2[a]));
        else update(1,n,1,p1[a]);
    }
    return 0;
}

CodeForces 620E 
题目传送门：http://codeforces.com/problemset/problem/620/E 
给你一棵树，每个节点都有颜色，然后问你子树上有多少种不同的颜色 
考虑到颜色一共只有60种，所以可以直接二进制记录，每个节点记录这个节点的颜色，然后区间直接左右子树或起来，然后对x为根的子树都变成c颜色，区间赋值，需要pushdown，pushup。 
有个坑点就是需要记录每个时间戳是哪个点，然后在build线段树的时候，sum[rt]=c[dfsnum[l]]，这个坑点我错了好久，因为线段树的节点的下标应该是时间戳。GG，仍需努力 
代码：

#include <map>
#include <set>
#include <stack>
#include <queue>
#include <cmath>
#include <string>
#include <vector>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <sstream>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#pragma comment(linker, "/STACK:102400000,102400000")

using namespace std;
#define   MAX           400005
#define   MAXN          6005
#define   maxnode       15
#define   sigma_size    30
#define   lson          l,m,rt<<1
#define   rson          m+1,r,rt<<1|1
#define   lrt           rt<<1
#define   rrt           rt<<1|1
#define   middle        int m=(r+l)>>1
#define   LL            long long
#define   ull           unsigned long long
#define   mem(x,v)      memset(x,v,sizeof(x))
#define   lowbit(x)     (x&-x)
#define   pii           pair<int,int>
#define   bits(a)       __builtin_popcount(a)
#define   mk            make_pair
#define   limit         10000

//const int    prime = 999983;
const int    INF   = 0x3f3f3f3f;
const LL     INFF  = 0x3f3f;
const double pi    = acos(-1.0);
//const double inf   = 1e18;
const double eps   = 1e-8;
const LL    mod    = 1e9+7;
const ull    mx    = 133333331;

/*****************************************************/
inline void RI(int &x) {
      char c;
      while((c=getchar())<'0' || c>'9');
      x=c-'0';
      while((c=getchar())>='0' && c<='9') x=(x<<3)+(x<<1)+c-'0';
 }
/*****************************************************/

struct Edge{
    int v,next;
}edge[MAX*2];
int head[MAX];
int tot;
int c[MAX];
int p1[MAX];
int p2[MAX];
int ti;
int dfsnum[MAX];
LL sum[MAX<<2];
int col[MAX<<2];
void init(){
    mem(head,-1);
    tot=0;ti=0;
}

void add_edge(int a,int b){
    edge[tot]=(Edge){b,head[a]};
    head[a]=tot++;
}

void dfs(int u,int fa){
    p1[u]=++ti;
    dfsnum[ti]=u;
    for(int i=head[u];i!=-1;i=edge[i].next){
        int v=edge[i].v;
        if(v==fa) continue;
        dfs(v,u);
    }
    p2[u]=ti;
}

void pushup(int rt){
    sum[rt]=sum[lrt]|sum[rrt];
}

void pushdown(int rt){
    if(col[rt]){
        col[lrt]=col[rrt]=col[rt];
        sum[lrt]=sum[rrt]=(1LL<<col[rt]);
        col[rt]=0;
    }
}
void build(int l,int r,int rt){
    col[rt]=0;
    if(l==r){
        sum[rt]=(1LL<<c[dfsnum[l]]);
        return;
    }
    middle;
    build(lson);
    build(rson);
    pushup(rt);
}

void update(int l,int r,int rt,int L,int R,int d){
    if(L<=l&&r<=R){
        sum[rt]=(1LL<<d);
        col[rt]=d;
        return;
    }
    middle;
    pushdown(rt);
    if(L<=m) update(lson,L,R,d);
    if(R>m) update(rson,L,R,d);
    pushup(rt);
}

LL query(int l,int r,int rt,int L,int R){
    if(L<=l&&r<=R) return sum[rt];
    middle;
    LL ret=0;
    pushdown(rt);
    if(L<=m) ret|=query(lson,L,R);
    if(R>m) ret|=query(rson,L,R);
    return ret;
}

int main(){
    //freopen("in.txt","r",stdin);
    int n,m;
    while(cin>>n>>m){
        init();
        for(int i=1;i<=n;i++) scanf("%d",&c[i]);
        for(int i=1;i<n;i++){
            int a,b;
            scanf("%d%d",&a,&b);
            add_edge(a,b);
            add_edge(b,a);
        }
        dfs(1,-1);
        build(1,n,1);
        //cout<<query(1,n,1,p1[6],p2[6]);
        while(m--){
            int op,a;
            scanf("%d%d",&op,&a);
            if(op==1){
                int cc;
                scanf("%d",&cc);
                update(1,n,1,p1[a],p2[a],cc);
            }
            else {
                LL k=query(1,n,1,p1[a],p2[a]);
                //cout<<k<<" ";
                int num=0;
                while(k){
                    int tmp=k%2;
                    k/=2;
                    num+=tmp;
                    //if(tmp) cout<<tmp<<" ";
                }
                printf("%d
",num);
            }
        }
    }
    return 0;
}