AVL树、splay树(伸展树)和红黑树比较
一、AVL树:
优点:查找、插入和删除,最坏复杂度均为O(logN)。实现操作简单
如过是随机插入或者删除,其理论上可以得到O(logN)的复杂度,但是实际情况大多不是随机的。如果是随机的,则AVL 树能够达到比RB树更优的结果,因为AVL树的高度更低。如果只进行插入和查找,则AVL树是优于RB树的,因为RB树 更多的优势还是在删除动作上。
缺点:1)借助高度或平衡因子,为此需要改造元素结构,或额外封装-->伸展树可以避免。
2)实测复杂度与理论复杂度上有差距。插入、删除后的旋转成本不菲。删除操作后,最多旋转O(logN)次,(Knuth证明,平 均最坏情况下概率为0.21次),若频繁进行插入/删除操作,得不偿失。
3)单词动态调整后,全树拓扑结构的变化量可达O(logN)次。-->红黑树为O(1)
二、伸展树(splay tree)、
优点、1)无需记录节点高度和平衡因子,编程实现简单易行
2)分摊复杂度为O(logN)
3)局部性强,缓存命中率极高时,效率甚至可以更高。
注:伸展树是根据数据访问的局部性而来的主要是:1)刚刚被访问的节点,极有可能在不就之后再次被访问到;2)将被访问 的下一个节点,极有可能就处于不就之前被访问过的某个节点的附近。
缺点:1)仍不能保证单词最坏情况的出现,不适用效率敏感的场合
2)复杂度分析比较复杂
三、红黑树
优点:1)所有的插入、删除、查找操作的复杂度都是O(logN)
2)插入操作能够在最多2次旋转后达到平衡状态,而删除操作更是能够在一次旋转后达到平衡状态。删除操作有可能导致递归的双黑修正,但是在旋转之前,只是染色而树的结构没有任何实质性的改变,因此速度优于AVL树。
3)红黑树可以保证在每次插入或删除操作之后的重平衡过程中,全书拓扑结构的更新仅涉及常数个节点。尽管最坏情况下需对O(logN)个节点重染色,但就分摊意义而言,仅为O(1)个。
缺点:左右子树高度相差比AVL树大。
总结
二叉查找树:
任意一个节点所包含的键值,大于等于左孩子的键值,小于等于右孩子的键值。
此外,无论是左旋还是右旋,若旋转之前这棵树是二叉查找树,旋转之后它一定还是二叉查找树。
平衡树(AVL树):
AVL树中任何节点的两个子树的高度最大差别为1,LL,RR,LR,RL旋转算法。
对于1百万个节点的平衡树,树的高度为12-20之间,对于10亿个节点的平衡树,树的高度为18-30之间。
伸展树:
当某个节点被访问时,伸展树会通过旋转使该节点成为树根。
红黑树:
主要是用它来存储有序的数据,它的时间复杂度是O(lgn)),效率非常之高.
AVL树与红黑树比较:
AVL是严格平衡树,因此在增加或者删除节点的时候,根据不同情况,旋转的次数比红黑树要多。(所以AVL树插入和删除时间会稍微多)
红黑树是弱平衡的,用非严格的平衡来换取增删节点时候旋转次数的降低。
两者都属于自平衡二叉树,那么降低树的深度自然会提高查找效率。
两者查找,插入,删除的时间复杂度相同O(lgn)
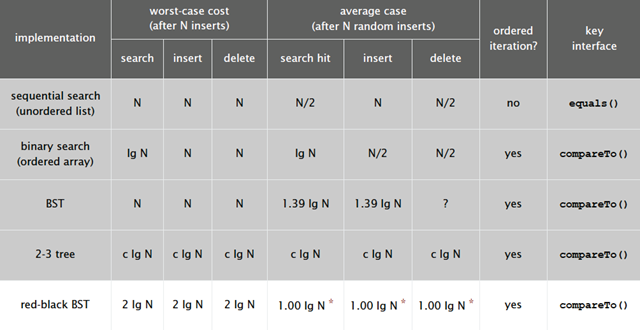
时间复杂度比较
sequential search - 顺序查找
binary search - 二分查找
BST - 二叉查找树
2-3 tree - 平衡树
red-black tree - 红黑树