2020/01/02 深度学习数学基础学习——朴素贝叶斯——生成式模型与判别式模型

朴素贝叶斯

Q1：朴素贝叶斯是用来干什么的？

朴素贝叶斯是一种实现 分类 的方法。用来从数据中学习预测模型，对新样本进行类别预测。

给定一个训练集 (T={(vec x_{1}, y_{1}), (vec x_{2}, y_{2}), ..., (vec x_{N}, y_{N})})，

朴素贝叶斯的目的是 根据数据集(T)，估计出联合概率分布 (P(vec X, Y)) 或者 类后验概率分布 (P(Y|vec X))，使得新的样本（不在训练集中的样本） (vec X_{new}) 来了之后，朴素贝叶斯能够根据上述分布预测出正确的 (y_{new})。

由于类后验概率分布 (P(Y|vec X)) 中，随机变量组合的情况实在太多了，要精准的描述后验分布需要大量的样本，这在现实中是不切实际的。

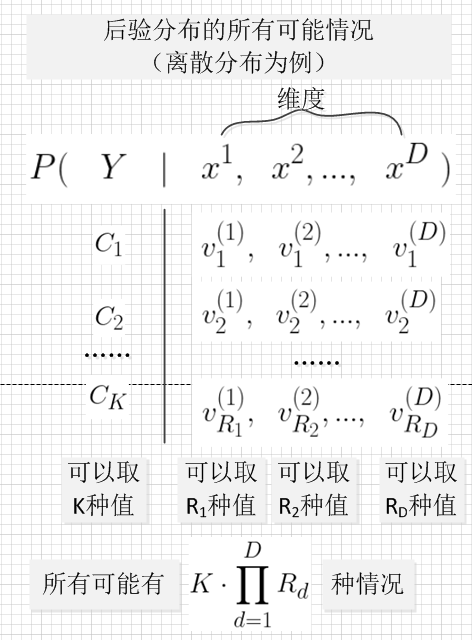
因此，我们需要通过有限的样本来估计类后验概率分布 (P(Y|vec X))

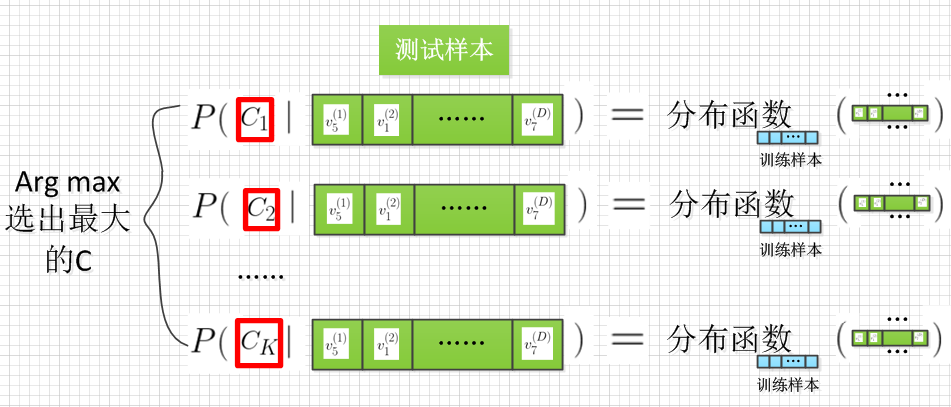
Q2：如何使用 类后验概率分布 (P(Y|vec X)) 来预测类别？

朴素贝叶斯的决策规则是，新样本 (vec x_{new}) 来了之后，从新样本的各个类后验概率中，选出使得后验概率最大的那个类 (Y=C_{max}) 作为预测结果。公式表达如下：

[arg max _{C_{k}} {P(Y=C_{1}|vec X=vec x_{new}), P(Y=C_{2}|vec X=vec x_{new}), ..., P(Y=C_{k}|vec X=vec x_{new})} ]

Q3：如何根据样本来学习 类后验概率分布 (P(Y|vec X)) ？

为了能够根据样本来学习类后验概率分布 (P(Y|vec X))，我们先对类后验概率分布 (P(Y|vec X))进行公式变形。根据贝叶斯规则：

[arg max _{C_{k}} P(Y=C_{k}|vec X) = arg max _{C_{k}} P(vec X | Y=C_{k}) cdot P(Y=C_{k}) ]

为了便于分析，我们把随机向量 (vec X) 逐维度拆开成各个维度的随机变量：

[arg max _{C_{k}} P(vec X | Y=C_{k}) cdot P(Y=C_{k}) = arg max _{C_{k}} P(x^{(1)}, x^{(2)}, ..., x^{(D)} | Y=C_{k}) cdot P(Y=C_{k}) ]

朴素贝叶斯有一个强假设——各个维度的随机变量之间特征独立，因此：

[arg max _{C_{k}} P(x^{(1)}, x^{(2)}, ..., x^{(D)} | Y=C_{k}) cdot P(Y=C_{k}) = arg max _{C_{k}} P(Y=C_{k}) cdot prod_{d=1}^{D}P(x^{(d)}| Y=C_{k}) ]

在上式中，
(P(Y=C_{k})) 是类先验概率，表示类 (C_{k}) 出现的概率。
(P(x^{(d)}| Y=C_{k})) 是类似然，它表示在 (C_{k}) 出现的情况下， 特征向量的第 (d) 维的值是 (x^{(d)}=v_{r}^{(d)})的概率，其中，(r) 表示在取值范围里的第 (r) 个取值。

在预测之前， 最最关键的一步 是先预先假设一个分布。比如：

[P(Y=C_{k})=分布函数_{C_{k}}() ]

[P(x^{(d)}| Y=C_{k}) = 分布函数_{C_{k}}(x_{样本1}^{(d)}, x_{样本2}^{(d)}, ..., x_{样本N}^{(d)}) ]

分布函数比如 高斯分布 (N(mu, heta))。

有了假设的分布，我们就可以利用训练样本来估计分布中的参数，从而建模(P(Y=C_{k})) 和 (P(x^{(d)}| Y=C_{k}))这两个分布 （这里面x是输入变量）。

为了简单起见，下面我们假设 (P(Y=C_{k})) 和 (P(x^{(d)}| Y=C_{k})) 都服从均匀分布，来看看朴素贝叶斯是如何利用数据来估计分布的。

• 对于类先验概率 (P(Y=C_{k})) ，我们可以用

[样本出现频率 = frac{训练样本中属于C_{k}的样本数量}{总训练样本数量} ]

   来表示，这里 (样本出现频率) 就是均匀分布中的参数，它就是由训练样本计算而来。

• 对于类似然 (P(x^{(d)}| Y=C_{k})) ，我们可以用

[样本出现频率 = frac{训练样本中，特征随机向量 vec X 第j维值为 v_{r}^{d}，且类别为 C_{k} 的样本数}{训练样本中类别为 C_{k} 的样本数} ]

   来表示，这里 (样本出现频率) 就是均匀分布中的参数，它就是由训练样本计算而来。

朴素贝叶斯的整体流程：

一些说明：

• 类别先验概率： (P(c))
  
• 类条件概率： (P(vec x | c)) ,其中(vec x=(x_{1},x_{2},...,x_{m}); m为属性)，(vec x)可以想象成特征向量
  举例: 当类别(c)是西瓜时，1号属性值(x_{1})为4的概率。
• 类别后验概率： (P(c|vec x) Leftrightarrow P(f_{vec heta}(vec x)|vec x) Leftrightarrow P(vec heta|vec x))（就是机器学习器）
  举例： 当1号属性值(x_{1})为4时，类别(c)是西瓜的概率。

生成式模型 与 判别式模型

强烈推荐资料：丨PRML中文版-第4.2节丨哔哩哔哩-李弘毅-机器学习2020丨

对于分类任务，我们知道了要通过 (arg max _{C_{k}} {P(Y=C_{k}|vec X=vec x)}) 来实现决策。

对于生成式模型

我们要 先预设是一个分布函数 （这个是我们自己设定，而不是学出来的），然后通过数据来确定分布函数的参数。这样就是说，我们对分布是什么有一个大致的感觉，只不过具体细节我们不清楚。

为了求下图中后验概率的分布。

• 第一步，我们要预先给定 (Pleft(x mid C_{1} ight)) 和 (Pleft(C_{1} ight)) 的分布。比如高斯分布，如下图。
  

• 第二步，用训练集数据来计算上述分布中的参数。比如对于上面的一维高斯分布 (N(mu, heta))，参数是 (mu) 就是一个参数，这个参数就可以通过训练数据得到：(mu = [ sum_{i=1}^{N} x_{训练样本i} / 样本数N ])

• 第三步，通过估算好的参数，(arg max _{C_{k}} {P(Y=C_{k}|vec X=vec x_{测试数据})}) 来实现决策。

对于上面的步骤，我们可以换一种形式：

这样，

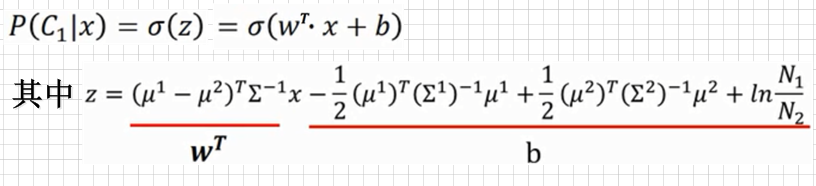
对于 生成式模型 ，我们要 先 预测 类条件分布(P(Y=C_{k}|vec X=vec x)) 的参数 (mu^{1}, mu^{2}, Sigma^{1}, Sigma^{2})，然后 再 得到 (W^{T}) 和 (b)。

对于判别式模型

没有人为预设分布函数的这一操作！！分布函数也是通过学习得来。这样就是说，我们完全不清楚分布是什么，不过我们也不care。

对于 判别式模型 ，我们直接建模(W^{T}) 和 (b)。不用中间步骤，这样其实就是不用人为预设分布函数。

资料

1. PRML中文版
2. 第三章 概率与信息论（deep learning 花书） + 第四章 朴素贝叶斯（统计学习方法） + 第七章 朴素贝叶斯（西瓜书）

备份

1. 文中图片的vsd文件