| Name | Date | Rank | Solved | A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020 Multi-University,Nowcoder Day 2 | 2020.7.18 | 78/1178 | 8/12 | O | O | O | O | O | O | O | Ø | × | × | × | O |
A.Clam and Fish(贪心)
题目描述
一共 (n(1leq nleq 2 imes 10^6)) 天,每天有下述四种状态中的一种:
- 无鱼无饵
- 无鱼有饵
- 有鱼无饵
- 有鱼有饵
有鱼可以拿鱼,有饵可以拿饵,无鱼可以用一个饵拿鱼,或什么都不做,四种操作只能选一个,求最多能拿多少鱼。
分析
首先明确,要是当前的状态有鱼,那么直接抓鱼。若当前为状态 (2),那么用鱼饵钓鱼显然不如直接抓鱼实惠;若当前状态为 (3),虽然可以获得鱼饵,但是获得鱼饵也是为了在将来花费这个鱼饵钓到鱼,问题是将来可能不会再有钓鱼的机会(鱼饵多余,已经是最后一天……),不如放弃这个鱼饵,直接抓鱼。
若当前状态没有鱼,那么鱼饵要尽量在没有蛤蜊的时候用掉,有蛤蜊的状态用来获取鱼饵。若当前状态为 (0),什么都没有;那么有鱼饵的话直接用来抓鱼,否则就什么都不做。若当前状态为 (1),如果没有鱼饵,那就不必思考,直接获取鱼饵;如果有鱼饵,再来考虑要不要钓鱼;因为鱼饵是为将来状态为 (0) 的时候准备的,如果钓鱼后,拥有的鱼饵足够将来状态为 (0) 的那几天使用,就可以放心地钓鱼,否则就将蛤蜊做成鱼饵。
值得一提的是,需要逆向预处理第 (i) 天后状态为 (0) 的天数,再正向进行贪心。
代码
/******************************************************************
Copyright: 11D_Beyonder All Rights Reserved
Author: 11D_Beyonder
Problem ID: 2020牛客暑期多校训练营(第三场) Problem A
Date: 8/14/2020
Description: Greedy
*******************************************************************/
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=2000005;
int _;
char days[N];
int n;
int leftover[N];
int bait,fish;
inline void init();
int main(){
for(cin>>_;_;_--){
scanf("%d%s",&n,days+1);
init();
int i;
for(i=n;i>=1;i--){
leftover[i]+=days[i]=='0';
leftover[i]+=leftover[i+1];
}
for(i=1;i<=n;i++){
if(days[i]=='0'){
//没鱼 没蛤蜊
if(bait){
//有鱼饵 可以抓鱼
bait--;
fish++;
}
}else if(days[i]=='1'){
//没鱼 有蛤蜊
if(!bait){
//没鱼饵 只能将蛤蜊做成鱼饵
bait++;
}else{
//有鱼饵 考虑要不要抓鱼
if(leftover[i]<bait){
//当前鱼饵足够在后面没鱼没蛤蜊的情况下抓鱼
//现在可以抓鱼
fish++;
bait--;
}else{
//做成鱼饵 在将来没鱼没蛤蜊的情况下抓鱼
bait++;
}
}
}else{
//有鱼直接抓 不能错失机会
fish++;
}
}
printf("%d
",fish);
}
return 0;
}
inline void init(){
bait=fish=0;
fill(leftover,leftover+n+2,0);
}
B.Classical String Problem(模拟)
题目描述
给一个字符串 (S),下标从 (1) 开始,(q) 次询问,每一组有一个字符 (op),一个数字 (x),当 (op=A) 时,输出当前字符串第 (x) 个字符;当 (op=M) 时,如果 (x>0),把字符串最左边的 (x) 个字符放到字符串右边,如果 (x<0),把字符串最右边 (|x|) 个字符放到字符串左边。
数据范围:(2leq |S|leq 2 imes 10^6,1leq qleq 8 imes 10^5)。
分析
小模拟,对于一个字符串,存在两种操作,一种是将字符串长度为 (x) 的前缀移动到后面,或者将后缀移动到前面,另一种是查询当前第 (x) 个字符是什么。对于前后缀的移动可以认为字符串是一个环形的,只要移动环形的入口位置即可,定义变量 (base) 为第(0)个字符,移动的时候让 (base) 加上 (x),查询的时候查询(base+x) 位置的字符。
代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
string str;
cin >> str;
int base = -1;
int len = str.size();
int n;
cin >> n;
while (n--)
{
char s[2];
int x;
scanf("%s%d", s, &x);
if (s[0] == 'A')
{
int tmp = base + x;
if (tmp < 0)
{
tmp += len * ((abs(tmp)) / len + 1);
}
tmp %= len;
putchar(str[tmp]);
putchar('
');
}
else
{
base += x;
}
}
return 0;
}
C.Operation Love(思维+模拟)
题目描述
给出一个手掌的形状((20) 个点),判断图形是左手还是右手(可能旋转 (45^{circ}),但大小不会变化)。
分析
首先观察得仅存在一个点((O)):大拇指根部的点,与其相连的两条边长度分别是 (6) 和 (9),那么遍历所有的点,找到其与相邻两点之间的距离,最终定位到点 (O),并将整个图形进行平移,让点 (O) 与原点重合,与(O) 相连的两个边形成一个直角,此时只需要判断与 (O) 相邻的两个点在坐标轴上的关系即可判断是左右手。
代码
#include<bits/stdc++.h>
using namespace std;
typedef double db;
struct node
{
db x, y;
};
node input[20];
node num[20];
int qq, hj;
db dis(node& a, node& b)
{
return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
void trans()
{
int base = 0;
for (int i = 0; i < 20; i++)
{
int l = (i - 1 + 40) % 20;
int r = (i + 1) % 20;
db ll = dis(input[i], input[l]);
db rr = dis(input[i], input[r]);
if ((fabs(ll - 9.0) < 1e-2 && fabs(rr - 6.0) < 1e-2) || (fabs(ll - 6.0) < 1e-2 && fabs(rr - 9.0) < 1e-2))
{
base = i;
break;
}
}
for (int i = 0; i < 20; i++)
{
num[i] = input[(i + base) % 20];
}
for (int i = 19; i >= 0; i--)
{
num[i].x -= num[0].x;
num[i].y -= num[0].y;
}
if (fabs(dis(num[0], num[1]) - 9.0) < 1e-2)
{
hj = 1;
qq = 19;
}
else
{
hj = 19;
qq = 1;
}
}
int main()
{
int t;
cin >> t;
while (t--)
{
for (int i = 0; i < 20; i++)
{
scanf("%lf%lf", &input[i].x, &input[i].y);
}
trans();
node chang = num[hj];
node duan = num[qq];
bool wa = false;
if (duan.x >= 0.0 && duan.y > 0.0)
{
if (chang.x > 0.0 && chang.y <= 0.0)wa = true;
}
else if (duan.x > 0.0 && duan.y <= 0.0)
{
if (chang.x <= 0.0 && chang.y < 0.0)wa = true;
}
else if (duan.x <= 0.0 && duan.y < 0.0)
{
if (chang.x < 0.0 && chang.y >= 0.0)wa = true;
}
else
{
if (chang.x >= 0.0 && chang.y > 0.0)wa = true;
}
if (wa)puts("right");
else puts("left");
}
return 0;
}
D.Points Construction Problem(构造)
题目描述
在二维平面内,每个格点(整数点)有一个白点,可以将其中一些点涂黑。问能否将 (n(1leq nleq 50)) 个白点涂黑,使得有 (m(1leq mleq 200)) 对相邻的白点和黑点(相邻指曼哈顿距离为 (1))。
分析
在平面上用小正方形构造一个可以分散的,面积为 (n),周长和为 (m) 的不规则图形。首先考虑 (n) 与 (m) 的关系,显然,当 (n) 个小正方形互相不接触的时候是周长和最大的情况,此时 (m=4 imes n),当 (n) 个小正方形尽可能堆积成一个大正方形的时候,周长是最小的,此时 (m=2 imes(lceilsqrt{n} ceil+lceilfrac{n}{lceilsqrt{n} ceil} ceil)),另外,考虑对于每一个不规则图形的一条边,总存在另一条边与其对应,周长应该总是一个偶数,当 (m) 是奇数的时候同样无法构造答案。
具体构造方法,可以认为一开始所有的小正方形都是排列在一条斜线上的,此时总周长是 (4 imes n),此时可以将后面的小正方形一个个取出来,放在与前面正方形相接触的位置,如果放置的位置与一个正方形相接触,总周长 (-2),如果和两个接触,总周长 (-4)。再考虑要保证能够构造出周长最小的情况,因此需要一层一层来膜最开始的一个正方形,具体构造顺序可以认为如下:
| 1 | 2 | 5 | 10 | 17 |
|---|---|---|---|---|
| 3 | 4 | 6 | 11 | 18 |
| 7 | 8 | 9 | 12 | 19 |
| 13 | 14 | 15 | 16 | 20 |
| 21 | 22 | 23 | 24 | 25 |
一直按这样的顺序来构造,直到最后总周长等于 (m) 的时候停止,此时剩余的所有方块在一个较远的位置摆放成一条斜线。需要特别注意,如果某一时刻要构造的位置会让周长减 (4),但是此时周长和 (m) 的差值只有 (2),可以特别地在第一个方块的上面放一个方块,然后结束构造,即可规避这种特殊情况。
代码
#include<bits/stdc++.h>
using namespace std;
int mp[50][50];
int main()
{
int t;
cin >> t;
while (t--)
{
memset(mp, 0, sizeof(mp));
int n, m;
scanf("%d%d", &n, &m);
if (m & 1 || m > 4 * n)
{
puts("No");
continue;
}
int tmp = 4 * n - m;
mp[1][1] = 1;
int step = 2;
while (tmp && step <= 10)
{
int tt = 2 * step - 1;
tt *= 4;
tt -= 4;
if (tmp >= tt)
{
for (int i = 1; i <= step; i++)
{
mp[step][i] = mp[i][step] = 1;
}
step++;
tmp -= tt;
continue;
}
if (tmp)
{
mp[step][1] = 1;
tmp -= 2;
}
int cnt = 2;
while (tmp >= 4 && cnt < step)
{
mp[step][cnt] = 1;
tmp -= 4;
cnt++;
}
if (tmp)
{
mp[1][step] = 1;
tmp -= 2;
}
cnt = 2;
while (tmp >= 4 && cnt <= step)
{
mp[cnt][step] = 1;
tmp -= 4;
cnt++;
}
if (tmp)
{
mp[0][1] = 1;
tmp -= 2;
}
step++;
}
int sum = 0;
for (int i = 0; i <= 10; i++)
{
for (int j = 0; j <= 10; j++)
{
if (mp[i][j])sum++;
}
}
if (sum > n)puts("No");
else
{
puts("Yes");
n -= sum;
for (int i = 0; i <= 10; i++)
{
for (int j = 0; j <= 10; j++)
{
/*if (mp[i][j])
printf("■");
else printf(" ");*/
if (mp[i][j])
printf("%d %d
", i, j);
}
/*putchar('
');*/
}
for (int i = 0; i < n; i++)
{
printf("%d %d
", i + 1000, i + 1000);
}
}
}
return 0;
}
E.Two Matchings(dp)
题目描述
(p=[p_1,p_2,cdots,p_n]) 是一个长为 (n) 的全排列。
定义一个全排列是一个 匹配,当且仅当 (forall i,p_i eq i 且 p_{p_i}=i)。
对于数组 (a=[a_1,a_2,cdots,a_n](0leq a_ileq 10^9,ngeq 4)) 且 (n) 是偶数,定义全排列的价值为 (frac{displaystylesum_{i=1}^{n}Big|a_i-a_{p_i}Big|}{2})。
定义两个 匹配 (p,q) 是 可组合 的,当且仅当 (forall i,p_i eq q_i)。
找到两个 可组合 的 匹配,使得这两个 匹配 的总价值尽可能小,输出价值之和。
数据范围:(n) 的总和不超过 (2 imes 10^5,0leq a_ileq 10^9)。
分析
要想使总价值最小,需要找到价值最小的排列和价值最小的排列。
价值最小的排列很容易找到,把 (a) 序列排序后两两配对计算价值即可。
下文中均假设序列已经排好序。
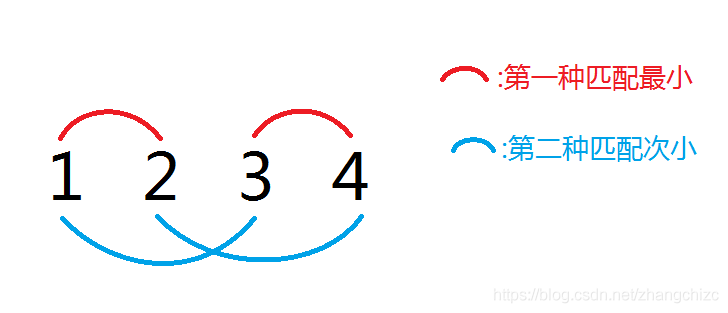
对于 (a) 序列有 (4) 个数字的情况,可以发现次小价值为 (a[4]-a[2]+a[3]-a[1]=a[4]+a[3]-a[2]-a[1])。
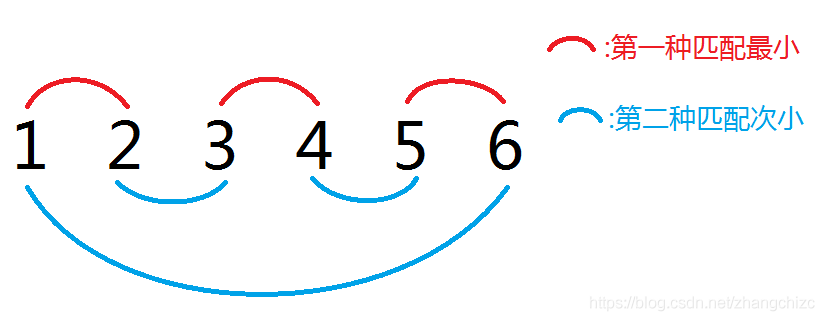
对于有 (a) 序列 (6) 个数字的情况,可以发现次小价值为 (a[3]-a[2]+a[5]-a[4]+a[6]-a[1])。
对于更长的序列,一定可以拆分成长为 (4) 和长为 (6) 的序列,转化成了子问题。
设 (dp[i]) 为前 (i) 个数的次大 价值。
状态转移方程为:
代码
#include<bits/stdc++.h>
using namespace std;
const int N=200100;
const long long INF=1ll<<60;
long long a[N],dp[N];
int main()
{
int T;
cin>>T;
while(T--)
{
long long ans=0,n;
scanf("%lld",&n);
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]);
sort(a+1,a+1+n);
for(int i=2;i<=n;i=i+2)
ans=ans+a[i]-a[i-1];
dp[2]=INF;
dp[4]=a[4]+a[3]-a[2]-a[1];
dp[6]=a[6]+a[5]+a[3]-a[4]-a[2]-a[1];
for(int i=8;i<=n;i=i+2)
dp[i]=min(dp[i-4]+a[i]+a[i-1]-a[i-2]-a[i-3],dp[i-6]+a[i]+a[i-1]+a[i-3]-a[i-2]-a[i-4]-a[i-5]);
printf("%lld
",ans+dp[n]);
}
return 0;
}
F.Fraction Construction Problem(exgcd+构造)
题目描述
给出两个数字 (a,b(1leq a,bleq 2 imes 10^6)),求任意一组满足下列条件的 (c,d,e,f):
-
(frac{c}{d}-frac{e}{f}=frac{a}{b})
-
(d<b,f<b)
-
(1leq c,eleq 4 imes 10^{12})
若无解,输出 (-1 -1 -1 -1),(1leq Tleq 10^5)。
分析
若 (gcd(a,b) eq 1) 时,令 (c=2a,d=b,e=a,f=b)。
若 (b=1),无解。
若 (gcd(a,b)=1):
令 (df=kb)((k) 为正整数)。
若 (b) 是质数,无解,因为 (b) 的因子只有 (1) 和 (b),(d) 和 (f) 只能取 (b) 的倍数,与 (d<b,f<b) 矛盾。
若 (b) 是某个质数的幂次方(即 (p^k)),无解。设 (b=p^k,d=p^a),则 (f=p^{k-a}),由扩展欧几里得算法可知 (cf-de=a) 的充要条件是 (gcd(d,f)|a),所以 (gcd(d,f)=p^{min(a,k-a)})。但是由于 (gcd(a,b)=1),所以 (p mid a),即 (gcd(d,f)|a),与前面所述矛盾。
所以 (b) 至少有两个质因子才有解,假设 (b=p_1^{k_1}p_2^{k_2}),则 (d=p_1^{k_1-1}p_2^{k_2},f=p_1^{k_1}),解方程 (p_1c+p_2^{k_2}e=1),解出 (c,e) 后,都乘上 (a),则:
代码
#include<bits/stdc++.h>
using namespace std;
long long T,a,b;
long long exgcd(long long a,long long b,long long &x,long long &y)
{
if(!b)
{
x=1;
y=0;
return a;
}
long long gcd=exgcd(b,a%b,x,y);
long long temp=x;x=y;y=temp-(a/b)*y;
return gcd;
}
const int N=2e6+10;
long long fac[N+10];
bool vis[N+10];
void init()
{
for(int i=2;i<=N;i++)
{
if(!vis[i])
{
for(int j=i;j<=N;j=j+i)
{
if(!vis[j])
fac[j]=i;
vis[j]=1;
}
}
}
}
int main()
{
init();
long long T;
cin>>T;
while(T--)
{
long long a,b;
scanf("%lld %lld",&a,&b);
long long gcd=__gcd(a,b);
a=a/gcd;b=b/gcd;
if(gcd>1)
{
printf("%lld %lld %lld %lld
",a*2,b,a,b);
continue;
}
if(b==1)
{
printf("-1 -1 -1 -1
");
continue;
}
gcd=b;
while(gcd%fac[b]==0)
gcd=gcd/fac[b];
if(gcd==1)
{
printf("-1 -1 -1 -1
");
continue;
}
long long c;
long long d=b/fac[b];
long long e;
long long f=b/gcd;
exgcd(fac[b],gcd,c,e);
c=c*a;
e=e*a;
e=-e;
if(c<0)
{
swap(c,e);
swap(d,f);
c=-c;e=-e;
}
printf("%lld %lld %lld %lld
",c,d,e,f);
}
return 0;
}
G.Operating on a Graph(并查集+启发式合并)
题目描述
给一个 (n) 个点,(m) 条边的无向图。点的编号从 (0) 到 (n-1)。一开始,点 (i) 属于团 (i)。定义团 (A) 与团 (B) 相连,当且仅当属于团 (A) 的点和属于团 (B) 的点之间至少有一条边相连。给定 (q) 次操作,每次操作给出 (o_i)。如果没有边属于团 (o_i),无事发生;否则所有与 (o_i) 相连的点都属于团 (o_i)。最后输出每个点属于哪个团。
数据范围:(2leq nleq 8 imes 10^5,1leq mleq 8 imes 10^5,1leq qleq 8 imes 10^5)。
分析
可以发现,每个点被询问后,该点与其相邻点永远处于相同集合。
用并查集维护每个点属于哪个集合,再用 (vector) 存储该集合的外部连接点是哪几个。更新外部连接点的时候按照集合大小来合并,不然超内存。
代码
#include<bits/stdc++.h>
using namespace std;
int fa[800010];
int get(int x)
{
if(fa[x]==x)
return x;
return fa[x]=get(fa[x]);
}
vector<int> G[800010];
int main()
{
int T;
cin>>T;
while(T--)
{
int n,m;
scanf("%d %d",&n,&m);
for(int i=0;i<=n;i++)
{
fa[i]=i;
G[i].clear();
}
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d %d",&u,&v);
G[u].push_back(v);
G[v].push_back(u);
}
int q;
scanf("%d",&q);
while(q--)
{
int o;
scanf("%d",&o);
if(fa[o]!=o)
continue;
vector<int> new_G=G[o];
G[o].clear();
for(int i=0;i<new_G.size();i++)
{
int v=get(new_G[i]);
if(v!=o)
{
fa[v]=o;
if(G[o].size()<G[v].size())//启发式合并
swap(G[o],G[v]);
for(int j=0;j<G[v].size();j++)
G[o].push_back(G[v][j]);
}
}
}
for(int i=0;i<n;i++)
printf("%d ",get(i));
puts("");
}
return 0;
}
H.Sort the Strings Revision(笛卡尔树+分治)
题目描述
给定一个初始字符串 (s_0),长度为 (n),第(i)个字符是 (i\%10),给定一个序列 (p) 和一个字符数组 (d),存在字符串 (s_1) ~ (sn),对于每一个字符串 (s_i),可以由前一个字符串 (s_{i-1}) 通过将第 (p[i-1]) 个位置的字符更改为 (d[i]) 来构造。将 (s_0) ~ (s_n) 按照字典序排序。
输入格式
(T(1leq Tleq 10^3)) 组数据,首先输入 $n(1leq nleq 2 imes 10^6) $ 代表字符串长度以及需要构造的 (p),(d) 的长度,随后依次给出 (p_{seed},p_a,p_b,p_{mod}(0leq p_{seed},p_a,p_b<p_{mod}leq 10^9+7)),(d_{seed},d_a,d_b,d_{mod}(0leq d_{seed},d_a,d_b< d_{mod}leq 10^9+7) 按照
的方式构造序列 (p),按照
的方式构造序列 (d),最终将 (n+1) 个字符串按照字典序从小到大将下标排序之后,输出(displaystyle{(sum_{i=0}^{n}(r_i*10000019^i))\%1000000007})。
输出格式
考虑 (n+1) 个字符串,相邻两两之间最多只有一个字符不相同,而且每个字符只会被修改一次,修改之后可能会使字符串字典序变大,变小,也有可能完全不变。首先不考虑不变的情况,显然,对于第 (0) 个字符,当它发生改变的时候,可能会导致后面所有的字符串字典序变大或者变小,但是不论怎么变化,都会以当前位置为分界,将 (n+1) 个字符分成大小两段,而且不论两段内部如何排序,总是满足某一段的所有字符串大于另一段的所有字符串。在拆分后的任意一段内,可以再次找到最靠前的一个被修改的字符,继续将字符串分割成两部分,如此递归下去,便能得到所有字符串的大小关系。再考虑那些不对字符串字典序产生影响的改变,可以对这些改变忽视,只对有效的修改进行拆分,最终会得到数个小片段,一些小片段可能包含不止一个字符串,这些片段产生的原因就是那些没有发生改变的修改,对于这些字符串,根据题目要求,按照下标升序进行排列即可。
对于序列 (p) 建立笛卡尔树,便能在 (O(n)) 的时间内处理出每一次分治的位置,为了使那些不产生影响的修改被忽视,可以将对应位置的 (p) 中元素赋值为一个极大值,这样在笛卡尔树建立的过程中会将他们下沉到整个树的最低端,也就不会对上面的分治产生影响。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1000000007;
const int maxn = 2000005;
const int inf = 0x7fffffff;
int st[maxn], l[maxn], r[maxn];
int p[maxn], d[maxn];
int rk[maxn];
void Cartesian(int n)//建笛卡尔树
{
int top = 0;
for (int i = 0; i < n; i++)
{
//l[i] = r[i] = -1;
while (top && p[st[top]] > p[i])
{
l[i] = st[top--];
}
if (top)
{
r[st[top]] = i;
}
st[++top] = i;
}
}
void dfs(int n, int L, int R, int rak)//分治
{
if (p[n] == inf || L >= R)//当前片段仅有一个元素或者当前片段的修改无效,可以按下表顺序进行赋值
{
for (int i = L; i <= R; i++)rk[i] = rak + i - L;
return;
}
dfs(l[n], L, n, rak + (p[n] % 10 > d[n]) * (R - n));
dfs(r[n], n + 1, R, rak + ((p[n] % 10 < d[n]) * (n - L + 1)));
}
int main()
{
int t;
cin >> t;
while (t--)
{
int n;
scanf("%d", &n);
ll pseed, pa, pb, pmod, dseed, da, db, dmod;
scanf("%lld%lld%lld%lld%lld%lld%lld%lld", &pseed, &pa, &pb, &pmod, &dseed, &da, &db, &dmod);
for (int i = 0; i < n; i++)//构造p
{
p[i] = i;
}
ll seed = dseed;
for (int i = 0; i < n; i++)
{
d[i] = seed % 10;
seed = (seed * da + db) % dmod;
}
seed = pseed;
for (int i = 1; i < n; i++)
{
swap(p[seed % (i + 1)], p[i]);
seed = (seed * pa + pb) % pmod;
}
for (int i = 0; i < n; i++)
{
if (p[i] % 10 == d[i])p[i] = inf;//如果p[i]位置的字符就是d[i]的话,此次修改无意义,赋值p[i]为极大值
}
Cartesian(n);
memset(rk, 0, sizeof(int) * (n + 1));
dfs(st[1], 0, n, 0);
ll ans = 0, tmp = 1;
for (int i = 0; i <= n; i++)
{
ans = (ans + (ll)rk[i] * tmp % mod) % mod;
tmp *= 10000019LL;
tmp %= mod;
}
printf("%lld
", ans);
}
return 0;
}
L.Problem L is the Only Lovely Problem(签到)
题目描述
给一个字符串,判断开头六个字符是不是 (lovely)(不区分大小写)。
分析
签到。
代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
string str;
cin >> str;
for (int i = 0; i < str.size(); i++)
{
str[i] = tolower(str[i]);
}
if (str.substr(0, 6) == "lovely")puts("lovely");
else puts("ugly");
return 0;
}