DS博客作业02--栈和队列

这个作业属于哪个班级	数据结构--网络2011/2012
这个作业的地址	DS博客作业02--栈和队列
这个作业的目标	学习栈和队列的结构设计及运算操作
姓名	韩龙飞

0.PTA得分截图

1.本周学习总结（0-5分）

1.1 栈

定义：栈是一种只能在一端进行插入或删除操作的线性表。
组成成分：栈顶（Top）、栈底(Bottom)
特点：后进先出（Last In First Out，LIFO）
基本操作：初始化、销毁、进栈、出栈、取栈顶元素

1.1.1 顺序栈

• 结构体

typedef struct                 
{
   ElemType data[MaxSize];
   int top;   //栈顶指针
}Stack,*SqStack;

• 初始化函数

void InitStack(SqStack &s) {
	s = new Stack;
	s->top = -1;
}

• 进栈
  

bool Push(SqStack &s, ElemType e) {
	if (s->top == MaxSize-1) {
		return false;
	}
        s->top++;
	s->data[s->top] = e;
	return true;
}

• 出栈
  

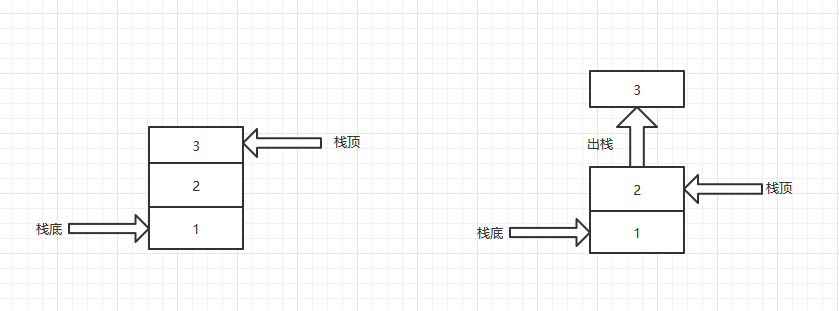
bool Pop(SqStack &s, ElemType e) {
	if (s->top == -1) {
		return false;
	}
	e=s->data[s->top];
        s->top--
	return true;
}

• 取栈顶元素
  

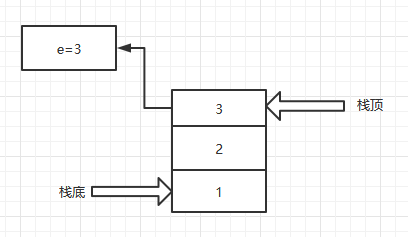
bool GetTop(SqStack &s, ElemType e) {
	if (s->top == -1) {
		return false;
	}
	e = s->data[s->top];
	return true;
}

1.1.2 链栈

• 结构体

typrdef struct linkNode
{
   ElemType data;
   struct linkNode *next;
}LiNode,*Listack;

• 初始化

void CreatStack(LiStack &s)
{  
   s=new LiNode;
   s->next=NULL;
}

• 进栈
  

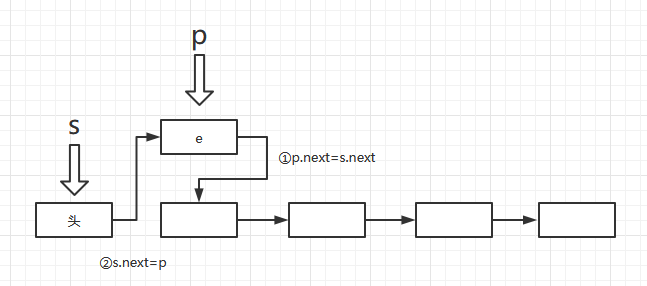
void Push(LiStack& S, ElemType e)
{
	LiStack p;
	p = new LiNode;
	p->data = e;
	p->next = S->next;
	S->next = p;
}

• 出栈
  

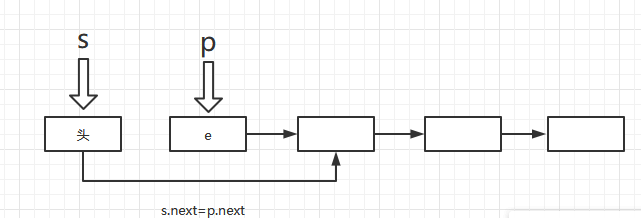
bool Pop(LiStack& S, ElemType e)
{
	LiStack p;
	if (S->next == NULL)return false;
	p = S->next;
	e = p->data;
	S->next = p->next;
	delete p;
	return true;
}

• 取栈顶元素

bool DetTop(LiStack& S, ElemType e)
{
	if (S->next == NULL)return false;
	e = S->next->data;
	return true;
}

1.2 栈的应用

1.2.1 将算术表达式转换为后缀表达式

优先级：(>*=/>+=- )不进栈

#include <string.h>
#include <iostream>
using namespace std;
struct Stacak {
    char* base;
    char* top;
    void Init(int m) 
    {
        base = (char*)malloc(m * sizeof(char));
        top = base;
    }
    void Pop() {
        --top;
    }
    void Push(char e) {
        *top++ = e;
    }
    bool Empty() {
        if (top == base) return true;
        return false;
    }
    char Top() {
        return *(top - 1);
    }
};
bool isNum(char c) 
{
    if (c == '.' || ('0' <= c && c <= '9')) return true;
    return false;
}
bool flag;
void pr() 
{
    if (flag) 
        printf(" ");
}
int main() {
    Stacak S;
    S.Init(1000);
    char s[1000];
    int p[1000];
    scanf("%s", s);
    p['*'] = p['/'] = 2;
    p['+'] = p['-'] = 1;
    while (!S.Empty()) {
        printf("%c
", S.Top());
        S.Pop();
    }
    for (int i = 0; s[i];) {
        if (s[i] == '+' || s[i] == '-') {
            if (i == 0) {// -1+3 
                if (s[i] == '-') {
                    printf("-");
                    flag = true;
                }
                i++;
                while (isNum(s[i])) {//处理多位
                    printf("%c", s[i]);
                    flag = true;
                    i++;
                }
            }
            else if (s[i - 1] == '(') {//1+(-2) 
                pr();
                if (s[i] == '-') {
                    printf("-");
                    flag = true;
                }
                i++;
                while (isNum(s[i])) {
                    printf("%c", s[i]);
                    flag = true;
                    i++;
                }
            }
            else if (s[i - 1] == '+' || s[i - 1] == '-' || s[i - 1] == '*' || s[i - 1] == '/') {//-1--1
                pr();
                if (s[i] == '-') {
                    printf("-");
                    flag = true;
                }
                i++;
                while (isNum(s[i])) {
                    printf("%c", s[i]);
                    flag = true;
                    i++;
                }
            }
            else {
                while (!S.Empty() && p[S.Top()] >= p[s[i]] && S.Top() != '(') {
                    pr();
                    printf("%c", S.Top());
                    S.Pop();
                    flag = true;
                }
                S.Push(s[i]);
                i++;
            }
        }
        else if (s[i] == '*' || s[i] == '/') {
            while (!S.Empty() && p[S.Top()] >= p[s[i]] && S.Top() != '(') {
                pr();
                printf("%c", S.Top());
                S.Pop();
                flag = true;
            }
            S.Push(s[i]);
            i++;
        }
        else if ('0' <= s[i] && s[i] <= '9') {
            pr();
            while (isNum(s[i])) {
                printf("%c", s[i]);
                i++;
                flag = true;
            }
        }
        else if (s[i] == '(') {
            S.Push(s[i]);
            i++;
        }
        else if (s[i] == ')') {
            while (S.Top() != '(') {
                pr();
                printf("%c", S.Top());
                S.Pop();
                flag = true;
            }
            S.Pop();
            i++;
        }
    }
    while (!S.Empty()) {
        pr();
        printf("%c", S.Top());
        S.Pop();
        flag = true;
    }
    printf("
");
}

1.2.2 迷宫问题

利用栈可以存储先前走过的路径，当遇到死路时可返回以寻找新的可行路线，这种方法又叫回溯法。

#include <stdio.h>
#include<stdlib.h>
int mg[10][10]= {{1,1,1,1,1,1,1,1,1,1},
    {1,0,0,1,0,0,0,1,0,1},
    {1,0,0,1,0,0,0,1,0,1},
    {1,0,0,0,0,1,1,0,0,1},
    {1,0,1,1,1,0,0,0,0,1},
    {1,0,0,0,1,0,0,0,0,1},
    {1,0,1,0,0,0,1,0,0,1},
    {1,0,1,1,1,0,1,1,0,1},
    {1,1,0,0,0,0,0,0,0,1},
    {1,1,1,1,1,1,1,1,1,1}
};//地图
int M=8;//行数
int N=8;//列数
typedef struct
{
    int i;//当前方块行号
    int j;//当前方块列号
    int di;//下一个可走的相邻方块的方位号
} Box; //定义方块类型
typedef struct
{
    Box data[100];
    int top;//栈顶指针
} StType; //定义顺序栈类型
bool mgpath(int xi,int yi,int xe,int ye)//求解路径为：(xi,yi)->(xe,ye)
{
    int i,j,k,di,find;
    StType st;//定义栈st
    st.top=-1;//初始化栈顶指针
    st.top++;//初始方块进栈
    st.data[st.top].i=xi;
    st.data[st.top].j=yi;
    st.data[st.top].di=-1;
    mg[xi][yi]=-1;
    while(st.top>-1)//栈不为空时循环
    {
        i=st.data[st.top].i;
        j=st.data[st.top].j;
        di=st.data[st.top].di;//取栈顶方块
        if(i==xe&&j==ye)//找到出口，输出路径
        {
            printf("迷宫路径如下：
");
            for(k=0; k<=st.top; k++)
            {
                printf("	(%d,%d)",st.data[k].i,st.data[k].j);
                if((k+1)%5==0)
                    printf("
");
            }
            printf("
");
            return true;
        }
        find=0;
        while(di<4&&find==0)//站下一个可走方块
        {
            di++;
            switch(di)
            {
            case 0:
                i=st.data[st.top].i-1;
                j=st.data[st.top].j;
                break;
            case 1:
                i=st.data[st.top].i;
                j=st.data[st.top].j+1;
                break;
            case 2:
                i=st.data[st.top].i+1;
                j=st.data[st.top].j;
                break;
            case 3:
                i=st.data[st.top].i;
                j=st.data[st.top].j-1;
                break;
            }
            if(mg[i][j]==0)
                find=1;//找下一个可走相邻方块
        }
        if(find==1)//找到了下一个可走方块
        {
            st.data[st.top].di=di;//修改原栈顶元素的di值
            st.top++;//下一个可走方块进栈
            st.data[st.top].i=i;
            st.data[st.top].j=j;
            st.data[st.top].di=-1;
            mg[i][j]=-1;//避免重复走到该方块
        }
        else//没有路径可走则退栈
        {
            mg[st.data[st.top].i][st.data[st.top].j]=0;//让该位置变为其他路径可走方块
            st.top--;//将该方块退栈
        }
    }
    return false;
}
int main()
{
    if(!mgpath(1,1,M,N))
        printf("无解");
    return 0;
}

1.3 队列

定义：队列是一种只能在一端进行插入操作，在另一端进行删除操作的受限线性表
组成：队首（Front）、队尾（Rear）
特点：先进先出（First In First Out，FIFO）
基本操作：初始化、销毁、进队、出队、判断是否为空

1.3.1 顺序队

• 结构体

typedef struct {
	ElemType data[MaxSize];
	ElemType front, rear;
}Queue,*SqQueue;

• 初始化

void CreatQueue(SqQueue& Q) 
{
	Q == new Queue;
	Q->front = Q->rear = -1;
}

• 进队

bool EnQueue(SqQueue& Q, ElemType e)
{
	if (Q->rear + 1 == MaxSize)return false;
	Q->rear++;
        Q->data[Q->rear]=e;
	return true;
}

• 出队

bool DeQueue(SqQueue& Q, ElemType& e)
{
	if (Q->front == Q->rear)return false;
	Q->front++;
        e = Q->data[Q->front];        
	return true;
}

1.3.2 环形队列

顺序队的出队只是指针的挪动，并没有真正删除空间，因此由于队满条件的不严谨，会出现rear==MaxSize-1成立时队列中还有空位置的情况，这种现象称为假溢出
而环形队列可以解决这样的问题
与顺序队列不同的地方：
队头指针front循环增1：front=（front+1）%MaxSize
队头指针rear循环增1：rear=（rear+1）%MaxSize
队满：(rear+1)%MaxSize=front
初始化：rear=front=0

1.3.3 链队列

• 结构体

//定义节点结构
typedef struct node {
    ElemType data;
    struct node* next;
}QueueNode;
//定义头节点
typedef struct {
    QueueNode* front;
    QueueNode* rear;
}LinkQueue;

• 初始化

void InitQueue(LinkQueue* Q)
{
    Q->front = Q->rear = NULL;
}

• 进队

void EnLinkQueue(LinkQueue* Q, ElemType v)
{
    QueueNode* p;
    p = new QueueNode;
    p->data = v;
    p->next = NULL;
    if (QueueEmpty(Q))
        Q->front = Q->rear = p;
    else
    {
        Q->rear->next = p;  //将新的节点连接到队列
        Q->rear = p;             //指向队列尾
    }
}

• 出队

bool DeLinkQueue(LinkQueue* Q, ElemType &e)
{
    QueueNode* s;
    if (QueueEmpty(Q))return false;     
    s = Q->front;
    e = s->data;
    if (Q->front == Q->rear)   //判断队列是否只有一个节点
        Q->front = Q->rear = NULL;
    else
        Q->front = s->next;
    delete s;
    return true;
}

1.3.4 队列应用

1.3.4.1 报数问题

#include <stdio.h>
#include <malloc.h>
#define MaxSize 100
typedef int ElemType;
typedef struct 
{	ElemType data[MaxSize];				//存放队中元素
	int front,rear;						//队头和队尾指针
} SqQueue;								//顺序队类型
void InitQueue(SqQueue *&q)				//初始化队列
{	q=(SqQueue *)malloc (sizeof(SqQueue));
	q->front=q->rear=0;
}
void DestroyQueue(SqQueue *&q)			//销毁队列
{
	free(q);
}
bool QueueEmpty(SqQueue *q)				//判断队列是否为空
{
	return(q->front==q->rear);
}
bool enQueue(SqQueue *&q,ElemType e)	//进队列
{	if ((q->rear+1)%MaxSize==q->front)	//队满上溢出
		return false;
	q->rear=(q->rear+1)%MaxSize;
	q->data[q->rear]=e;
	return true;
}
bool deQueue(SqQueue *&q,ElemType &e)	//出队列
{	if (q->front==q->rear)				//队空下溢出
		return false;
	q->front=(q->front+1)%MaxSize;
	e=q->data[q->front];
	return true;
}
void number(int n)
{
	int i;  ElemType e;
	SqQueue *q;					//环形队列指针
	InitQueue(q);				//初始化队列
	for (i=1;i<=n;i++)			//构建初始序列
		enQueue(q,i);
	printf("报数出列顺序:");
	while (!QueueEmpty(q))		//队列不空循环
	{
		deQueue(q,e);			//出队一个元素e
		printf("%d ",e);		//输出元素编号
		if (!QueueEmpty(q))		//队列不空
		{
			deQueue(q,e);		//出队一个元素e
			enQueue(q,e);		//将刚出列的元素进队
		}
	}
	printf("
");
	DestroyQueue(q);			//销毁队列q
}
int main()
{
	int i,n=8;
	printf("初始序列:");
	for (i=1;i<=n;i++)
		printf("%d ",i);
	printf("
");
	number(n);
	return 0;
}

2.PTA实验作业（4分）

2.1 符号配对

2.1.1 解题思路及伪代码

伪代码

建栈s
输入字符串
for i=0 to str为空
    if 当前字符为左括号(大中小)
        进栈
    else if 当前字符为"/"下一个字符为"*"
        '<'进栈且i+1
    else if 当前字符为右括号(大或中或小）
        if 栈不为空且栈顶字符对应为左符号(大或中或小）
            出栈
        else
            输出no
            if 栈空
                打印规定格式字符(?-)
            else
                打印栈顶字符
            end if
        end if
    end if
    if 栈空且flag为1
        输出"YES"
    else if flag为0
        输出no和规定格式字符
end for

2.1.2 总结解题所用的知识点

①利用了库函数，节省自定义函数的时间
②栈空条件的判断要时刻注意
③利用栈的性质，栈顶元素一定是与右符号对应的左符号。

2.2 银行业务队列简单模拟

2.1.1 解题思路及伪代码

建两个队列qa和qb
定义整型变量n、number、e分别为顾客人数、编号、和存储数据变量
for i to n-1
    输入编号
    if 编号为偶数
        进qb队列
    else
        进qa队列
    end if
end for
for i to n-1
    if qa、qb不为空
        if i为0
            输出队首元素
        else
            if i%3等于2
                输出" "和qb队首元素
            else
                输出" "和qa队首元素
            end if
        end if
    end if
if qa为空qb不为空
    输出qb队首元素
end if
if qb为空qa不为空
    输出qa队首元素
end if

2.1.2 总结解题所用的知识点

①利用了队列函数
②利用队列特性先进先出

3.阅读代码（0--1分）

3.1 代码

class Solution {
public:
    void move(int n, vector<int>& A, vector<int>& B, vector<int>& C){
        if(n == 1){
            C.push_back(A.back());
            A.pop_back();
        } else{
            move(n - 1, A, C, B);
            move(1, A, B, C);
            move(n - 1, B, A, C);
        }
    }
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {        
        int n = A.size();        
        move(n, A, B, C);
    }
};

3.2 设计思路

利用了c++中的vector库函数，运用递归的方式把题目从n转化为了两块需要转移的部分

3.3 分析该题目解题优势及难点

优点：使用了vector库函数，利用了递归的解法
难点：递归的使用