DS博客作业04--图

这个作业属于哪个班级	数据结构--网络2011/2012
这个作业的地址	DS博客作业04--图
这个作业的目标	学习图结构设计及相关算法
姓名	韩龙飞

0.PTA得分截图

1.本周学习总结（6分）

1.1 图的存储结构

1.1.1 邻接矩阵

邻接矩阵是一种采用邻接矩阵数组表示顶点之间相邻关系的存储结构
邻接矩阵定义类型声明

#define MAXV <最大顶点个数>
#define INF 32767
typedef struct
{
	int no;//顶点编号
	InfoType info;//顶点其他信息
}VertexType;//顶点类型
typedef struct
{
	int edges[MAXV][MAXV];
	int n;//顶点
	int e;//边
	VertexType vexs[MAXV]//存放顶点信息
}MatGraph;

有向图
对于有向图来说，若存在一条边(i,j)，则此边只表示为从顶点i到顶点j，不可以由边(i,j)得到可以从顶点j到顶点i的信息。所以在建有向图的邻接矩阵时，只对edges[i][j]赋值(无权值，如果存在边就赋值为1，否则赋为0)；和无向图不一样的是，最后得到的邻接矩阵不一定是一个对称图形。

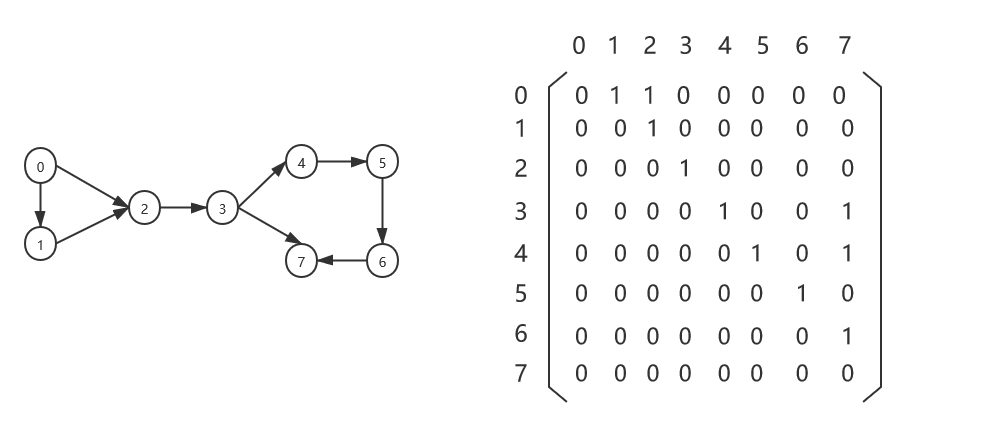
网
对于网来说，每一条边上都附有一个对应的数值————权，这时我们就不能像构造无权图的邻接矩阵一样，用1表示两个顶点之间存在边，用0表示两个顶点之间不存在边。因为权值可以是任意值。既然这样，不如我们直接保存所有边的权值，如果两个顶点之间没有边关系，直接赋为∞。

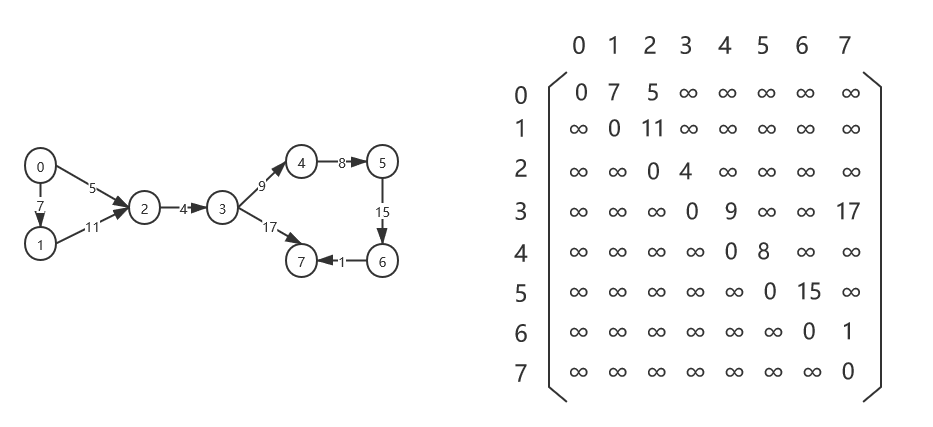
建图函数

/*无向图*/
void CreatGraph(MGraph*& g, int n, int e)
{
	int i, j, a, b;
	g = new MGragh;
	g->edges = new int* [n];
	for (i = 0; i < n; i++)
	{
		g->edges[i] = new int[n];
		for (j = 0; j < n; j++)
			g->edges[i][j] = 0;
	}
	for (i = 0; i < e; i++)
	{
		cin >> a >> b;
		g->edges[a][b] = g->[b][a] = 1;
	}
	g->n = n;
	g->e = e;
}
/*有向图*/
void CreatGraph(MGraph*& g, int n, int e)
{
	int i, j, a, b;
	g = new MGragh;
	g->edges = new int* [n];
	for (i = 0; i < n; i++)
	{
		g->edges[i] = new int[n];
		for (j = 0; j < n; j++)
			g->edges[i][j] = 0;
	}
	for (i = 0; i < e; i++)
	{
		cin >> a >> b;
		g->edges[a][b] = 1;
	}
	g->n = n;
	g->e = e;
}
/*网*/
void CreatGraph(MGraph*& g, int n, int e)
{
	int i, j, a, b;
	g = new MGragh;
	g->edges = new int* [n];
	for (i = 0; i < n; i++)
	{
		g->edges[i] = new int[n];
		for (j = 0; j < n; j++)
			g->edges[i][j] = INF;
	}
	for (i = 0; i < e; i++)
	{
		cin >> a >> b >> weight;
		g->edges[a][b] = weight;
	}
	g->n = n;
	g->e = e;
}

邻接矩阵特点
①图的邻接矩阵表示是唯一的
②无向图的邻接矩阵数组一定是对称矩阵，只需存放上下三角其中一部分即可
③对于无向图，邻接矩阵数组的第i行或第i列非零元素、非∞元素的个数正好是顶点i的度
④对于有向图，邻接矩阵数组的第i行或第i列非零元素、非∞元素的个数正好是顶点i的出度或入度

1.1.2 邻接表

邻接表是一种顺序与链式存储相结合的存储方法。
邻接表定义类型声明

ypedef struct ANode //边结点；
{
   int adjvex;//指向该边的终点编号；
   struct ANode*nextarc;//指向下一个邻接点；
   INfoType info;//保存该边的权值等信息；
}ArcNode;
typedef struct Vnode //头结点
{
   int data;//顶点；
   ArcNode *firstarc;//指向第一个邻接点；
}VNode;
typedef struct
{
   VNode adjlist[MAX];//邻接表；
   int n,e;//图中顶点数n和边数e；
}AdjGraph;

无向图

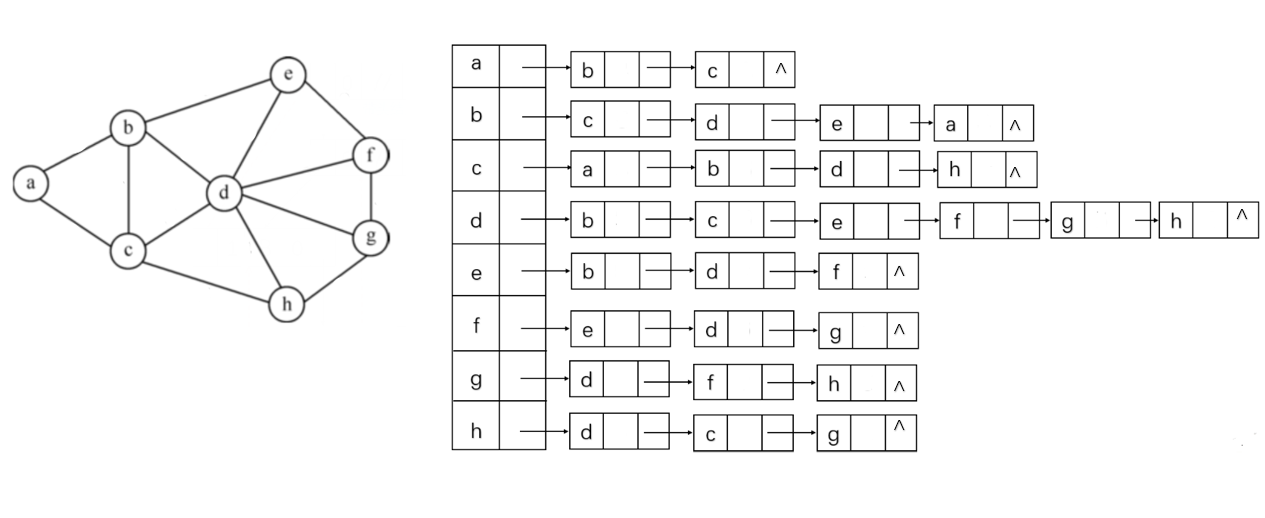
有向图

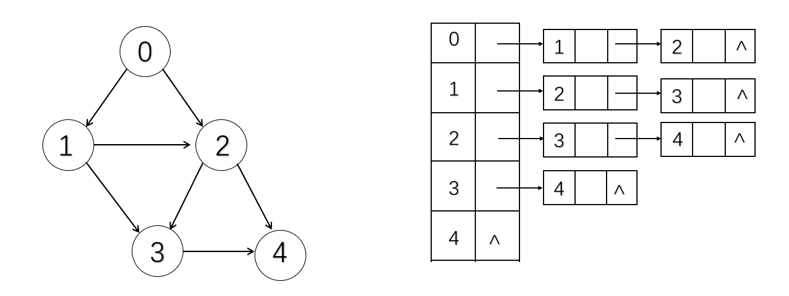
网

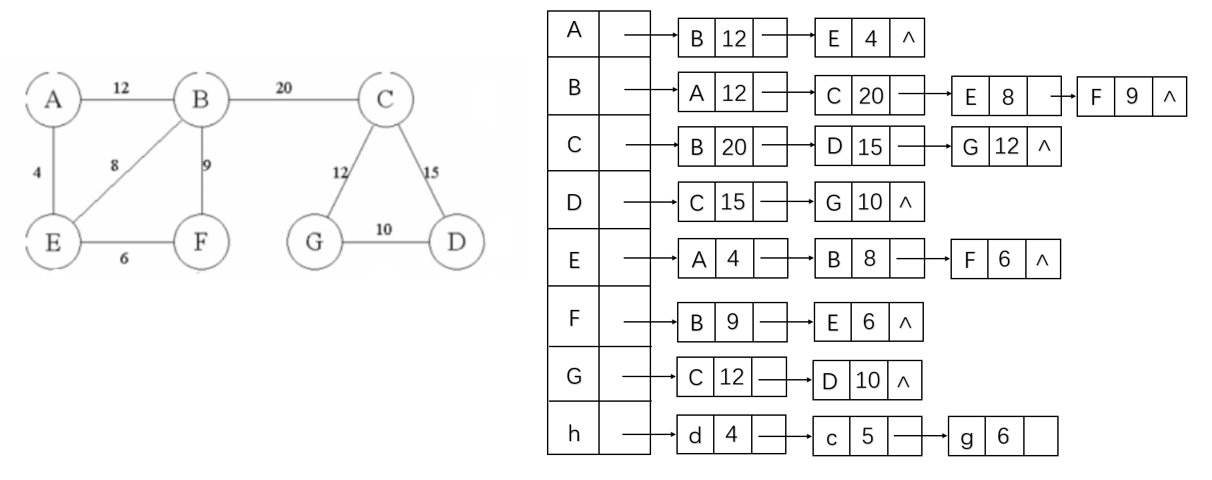
创建函数

/*无向图*/
void CreatAdjGraph(AdjGraph*& g, int n, int e)
{
	int i, j, a, b;
	ArcNode* p;
	g = new AdjGraph;
	g->adjlist = new VNode[n];
	for (i = 0; i < n; i++)
		g->adjlist[i].firstarc = NULL;
	for (i = 0; i < e; i++)
	{
		cin >> a >> b;
		p = new ArcNode;
		p->adjvex = b;
		p->nextarc = g->adjlist[a].firstarc;
		g->adjlist[a].firstarc = p;
		p = new ArcNode;
		p->adjvex = a;
		p->nextarc = g->adjlist[b].firstarc;
		g->adjlist[b].firstarc = p;
	}
	g->n = n;
	g->e = e;
}
/*有向图*/
void CreatAdjGraph(AdjGraph*& g, int n, int e)
{
	int i, j, a, b;
	ArcNode* p;
	g = new AdjGraph;
	g->adjlist = new VNode[n];
	for (i = 0; i < n; i++)
		g->adjlist[i].firstarc = NULL;
	for (i = 0; i < e; i++)
	{
		cin >> a >> b;
		p = new ArcNode;
		p->adjvex = b;
		p->nextarc = g->adjlist[a].firstarc;
		g->adjlist[a].firstarc = p;
	}
	g->n = n;
	g->e = e;
}
/*网*/
void CreatAdjGraph(AdjGraph*& g, int n, int e)
{
	int i, j, a, b;
	ArcNode* p;
	g = new AdjGraph;
	g->adjlist = new VNode[n];
	for (i = 0; i < n; i++)
		g->adjlist[i].firstarc = NULL;
	for (i = 0; i < e; i++)
	{
		cin >> a >> b >> weight;
		p = new ArcNode;
		p->adjvex = b;
		p->info = weight;
		p->nextarc = g->adjlist[a].firstarc;
		g->adjlist[a].firstarc = p;
	}
	g->n = n;
	g->e = e;
}

1.1.3 邻接矩阵和邻接表表示图的区别

对于一个具有n个顶点e条边的无向图
它的邻接表表示有n个顶点表结点2e个边表结点
对于一个具有n个顶点e条边的有向图
它的邻接表表示有n个顶点表结点e个边表结点
如果图中边的数目远远小于n2称作稀疏图，这是用邻接表表示比用邻接矩阵表示节省空间;
如果图中边的数目接近于n2,对于无向图接近于n*(n-1)称作稠密图,考虑到邻接表中要附加链域，采用邻接矩阵表示法为宜。

1.2 图遍历

1.2.1 深度优先遍历

深度优先遍历的过程是从图中的某个初始点v出发，然后选择一个与顶点v相邻且没被访问过的顶点w，以w为初始顶点，再从它出发进行深度优先遍历。直到途中与顶点v邻接的所有顶点都被访问过为止。

以下图为例

从顶点b开始进行深度优先遍历，可得序列b->c->a->d->e->f->g->h
步骤为
①访问顶点b，找b的相邻顶点c，c未被访问过，转向c；
②访问顶点c，找c的相邻顶点a，a未被访问过，转向a；
③访问顶点a，找a的相邻顶点，发现a的所有相邻顶点均被访问，则返回去c的下一个相邻顶点e；
…………
以此类推，最终可得如上序列。
代码如下：

void DFS(MGraph g, int v)
{
    int j;
    if (visited[v] == 0)
    {
        if (flag == 0)
        {
            cout << v;
            flag = 1;
        }
        else
            cout << " " << v;
        visited[v] = 1;
    }
    for (j = 1; j <= g.n; j++)
    {
        if (g.edges[v][j] && visited[j] == 0)
            DFS(g, j);
    }
}

1.2.2 广度优先遍历

广度优先遍历的过程是首先访问初始点v，接着访问顶点v的所有未被访问过的邻接点v1、v2、……vn,然后再按照v1、v2、……vn的次序访问每一个顶点的所有未被访问过的邻接点，直到所有和初始点有路径相通的顶点都被访问过。
从顶点b开始进行深度优先遍历，可得序列b->c->d->e->a->h->f->g
以下图为例

顶点b入队，找其第一个相邻顶点c，它未被访问过，访问并将c进队，找顶点c的下一个顶点d，它未被访问过，访问并进队…………

以此类推，最终可得如上序列。
代码如下：

void BFS(MGraph g, int v)
{
    int p;
    queue<int>q;
    if (visited[v] == 0)
    {
        cout << v;
        visited[v] = 1;
        q.push(v);
    }
    while (!q.empty())
    {
        p = q.front();
        q.pop();
        for (int j = 1; j <= g.n; j++)
        {
            if (g.edges[p][j] == 1 && visited[j] == 0)
            {
                cout << " " << j;
                visited[j] = 1;
                q.push(j);
            }
        }
    }
}

1.3 最小生成树

1.3.1 Prim算法求最小生成树

通过prim算法可得上图最小生成树的边序列为{<A,E><E,F><E,B><B,C><C,G><G,D>}
Prim的辅助数组
lowcost：用于存放最小路径
closest：
Prim函数

void Prim(MatGraph g, int v)
{
	int lowcost[MAXV];
	int i, j, k;
	for (i = 0; i < g.n; i++)
	{
		lowcost[i] = g.edges[v][i];
		closest[i] = v;
	}
	for (i = 1; i < g.n; i++)
	{
		MIN = INF;
		for (j = 0; j < g.n; j++)
		{
			if (lowcost[j] != 0 && lowcost[j] < MIN)
			{
				MIN = lowcost[i];
				k = j;
			}
		}
		lowcost[k] = 0;
		for(j=0;j<g.n;j++)
			if (lowcost[j] != 0 && g.edges[k][j] < lowcost[j])
			{
				lowcost[j] = g.edges[k][j];
				closest[j] = k;
			}
	}
}

Prim算法其时间复杂度为O(n^2)，执行时间与边得数目无关，适合稠密图.

1.3.2 Kruskal算法求解最小生成树

通过prim算法可得上图最小生成树的边序列为{<A,E><E,F><E,B><G,D><C,G><B,C>}

1.4 最短路径

1.4.1 Dijkstra算法求解最短路径

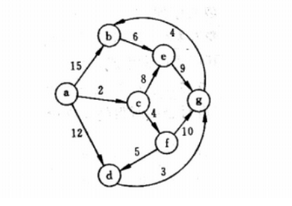
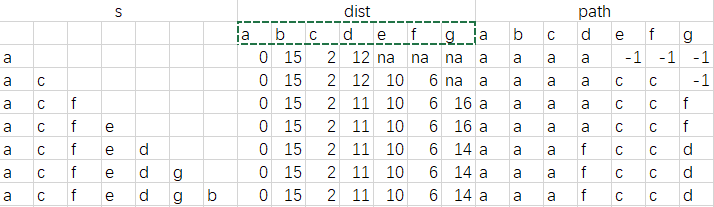
Dijkstra代码

void Dijkstra(MatGraph g, int v)
{
	int dist[MAXV]，path[MAXV];
	int s[MAXV];//判断是否访问
	int mindis, i, j, u;
	for (i = 0; i < g.n; i++)
	{
		dist[i] = g.edges[v][i];//初始化距离
		s[i] = 0;
		if (g.edges[v]]i] < INF)//v到i有边，初始化前继结点
		{
			path[i] = v;
		}
		else
		{
			path[i] = -1;
		}
	}
	s[v] = 1;
	for (i = 0; i < g.n; i++)//进行n-1次
	{
		mindis = INF;
		for (j = 0; j < g.n; j++)//找到最小路径的长度
		{
			if (s[j] == 0 && dist[j] < mindis)
			{
				u = j;
				mindis = dist[j];
			}
		}
		s[u] = 1;
		for (j = 0; j < g.n; j++)//修改改变结点后的路径长度
		{
			if (s[j] == 0)
			{
				if (g.edges[u][j] < INF&&dist[u] + g.edges[u][j] < dist[j])//修改此处可得到各种多种解法
				{
					dist[j] = dist[u] + g.edges[u][j];
					path[j] = u;
				}
			}
		}
	}
}

需要dist和path两个数组，其中dist数组用于存放最短的路径长度，通过比较其中元素找到最短路径，path数组则用于存放最短路径，通过改变path数组的值改变顶点的前继结点。
时间复杂度为O(n^2).

1.4.2 Floyd算法求解最短路径

代码实现

void Floyd(MatGraph g)
{
	int A[MAXV][MAXV];
	int path[MAXV][MAXV];
	int i, j, k;
	for (i = 0; i < g.n; i++)//进行初始化
	{
		for (j = 0; j < g.n; j++)
		{
			A[i][j] = g.edges[i][j];
			if (i != j && g.edgse[i][j] < INF)//存在边的关系时
			{
				path[i][j] = i;
			}
			else
			{
				path[i][j] = -1;
			}
		}
	}
	for (k = 0; k < g.n; k++)
	{
		for (i = 0; i < g.n; i++)
		{
			for (j = 0; j < g.n; j++)
			{
				if (A[i][j] > A[i][k] + A[k][j])//找到更短路径
				{
					A[i][j] = A[i][k] + A[i][j];//修改路径长度
					path[i][j] = k;//修改顶点
				}
			}
		}
	}
}

A和path两个二维数组，其中A数组是用于存放两个顶点之间的最短路径，path数组用于存放其的前继结点。
时间复杂度为O(n^3).

1.5 拓扑排序

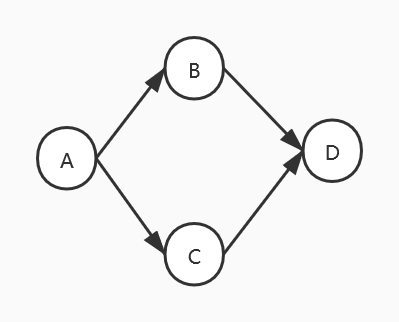
可得序列A->B->C->D或A->C->B->D
结构体

typedef struct {
	Vertex data;//顶点信息
	int count;//存放入度
	AreNode *firstarc;//头结点类型
}VNode;

代码实现

void TopSort(AdjGraph *G)
{
	int node[MAXV];
	int counts = 0;
	int top = -1;
	int stacks[MAXV];
	ArcNode *p;
	int i, j, k = 0;
	for (i = 0; i < G->n; i++)//初始化count
	{
		G->adjlist[i].count = 0;
	}
	for (i = 0; i < G->n; i++)
	{
		p = G->adjlist[i].firstarc;
		while (p)//计算每个结点入度
		{
			G->adjlist[p->adjvex].count++;
			p = p->nextarc;
		}
	}
	for (i = 0; i < G->n; i++)
	{
		if (G->adjlist[i].count == 0)//结点为0入栈
		{
			stacks[++top] = i;
		}
	}
	while (top > -1)
	{
		i = stacks[top--];
		node[k++] = i;//进入数组
		counts++;
		p = G->adjlist[i].firstarc;
		while (p)
		{
			j = p->adjvex;
			G->adjlist[j].count--;//该节点入度-1
			if (G->adjlist[j].count == 0)
			{
				stacks[++top] = j;
			}
			p = p->nextarc;
		}
	}
	if (counts < G->n)//判断个数是否符合
	{
		cout << "error!";
	}
	else
	{
		for (i = 0; i < k; i++)
		{
			cout << node[i];
			if (i != k - 1)
			{
				cout << " ";
			}
		}
	}
}

1.6 关键路径

• AOE网:带权的有向无环图，图中入度为0的顶点表示工程的开始事件，出度为0的顶点表示工程的结束事件，称这样的有向图为边表示活动的网(AOE网)。
• 通常每个工程都只有一个开始事件和结束事件，工程的AOE网都只有入度为0的顶点，称为源点，和一个出度为0的顶点，称为汇点。
• 关键路径:在AOE网中从源点到汇点的所有路径中最大路径长度的路径。
• AOE网中一条关键路径各活动持续时间的总和，把关键路径上的活动称为关键活动。

2.PTA实验作业（4分）

2.1 六度空间

2.1.1 解题思路

利用广度优先遍历，搜索距离小于6的结点，并用一个level实时记录，其中初始点的level值为0，当level值为6时循环结束

2.1.2 提交列表

2.1.3 本题知识点

• 广度优先遍历
• 图的创建

2.2 村村通

2.1.1 解题思路

对每一个点入队，更新到未入队的点的最短距离，也就是距离比原先的距离小就更新，这样每次对每个点更新，那么就能保证lowcost中的距离在当前状态下就是最小的，然后每次让距离最短的入队就可以了

2.1.2 提交列表

2.1.3 本题知识点

• 最小生成树的prim算法