用Venn Diagram(韦恩)图理解测试
用韦恩图表示软件规格确定的行为、程序实现的行为、被测试的行为:
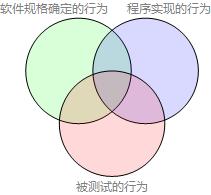
功能性测试把程序实现、系统实现看作黑盒,以软件规格说明为基础设计测试用例,测试效果的韦恩图如下:
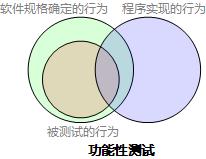
结构性测试即白盒测试,以程序实现代码为基础设计测试用例,测试效果的韦恩图如下:
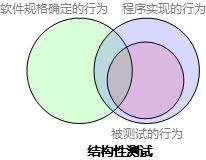
测试级别
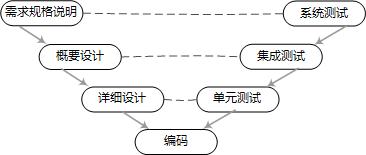
测试级别分为系统测试、集成测试、单元测试,分别与瀑布模型中的需求规格说明、概要设计、详细设计相对应,图示如下。一般情况下结构性测试适合在单元级别上进行,功能性测试适合在系统级别上进行
功能性测试 Functional Testing
1. 边界值测试 Boundary Value
边界值分析基于可靠性理论的单缺陷假设(失效极少是由两个或多个缺陷的同时发生引起的),在最小值、略高于最小值、正常值、略低于最大值、最大值处取输入变量值

健壮性测试则进一步引入max+和min-,测试超过极值时的系统反映
最坏情况测试则否认单缺陷假设,将多个变量在极值情况下进行组合测试,结合健壮性测试,则会在极值附近的+、-范围内进行组合测试
特殊值测试则基于经验、工程实践设计测试用例,这依赖测试人员的能力
随机测试则基于统计学理论,用随机数生成器选择测试用例值
边界值测试是初级的,适用于多个独立变量的函数,即变量之间不存在依赖性,并且边界值测试存在大量冗余
2. 等价类测试 Equivalent Class
例如测试fn(x1, x2), a<=x1<=d, e<=x2<=g
如果等价类区间划分为x1: [a, b), [b, c), [c, d]. x2: [e, f), [f, g],则弱一般等价类、强一般等价类的测试用例分别如下图所示:
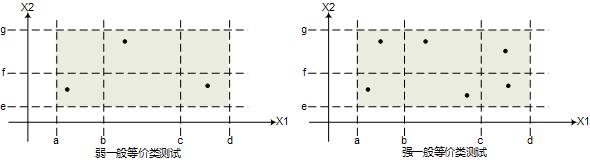
等价类测试的思想是: 对于同一个等价区间内的取值,其处理过程会是相同的,其关键在于识别等价类。弱一般等价类基于单缺陷假设,强一般等价类则基于多缺陷假设。弱健壮等价类、强健壮等价类则分别考虑无效值区间的情况
三角形问题的等价类测试
R1={<a, b, c>: 有三条边a,b,c的等边三角形}
R2={<a, b, c>: 有三条边a,b,c的等腰三角形}
R3={<a, b, c>: 有三条边a,b,c的非等腰三角形}
R4={<a, b, c>: 三条边a,b,c的等边不构成三角形}
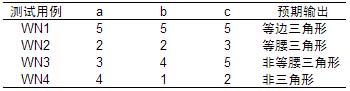
3. 基于决策表的测试 Decision Table-Based
与之相关的另外2种方法是Cause-Effect Graphing(因果图法)和Decision Tableau Method(决策表方法),这2种使用上复杂并且存在冗余。Decision Table-Based则是最严格的
决策表的基本结构

图片来自Cai Ferriday: A Review Paper on Decision Table-Based Testing
竖线左侧是桩stubs,右侧是条目entries;横线上方是条件conditions,下方是行为actions。entries部分每个列是一个rule,每一列中的值,conditions部分是输入值,actions部分表明输出值、期望结果
典型的决策表示例
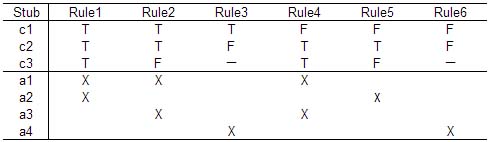
rules的第一列表明,如果条件c1,c2,c3都为true,则应当采取行动a1和a2;第二列表明如果c1,c2为true,c3为false,则应当采取行动a1和a3
三角形问题决策表示例
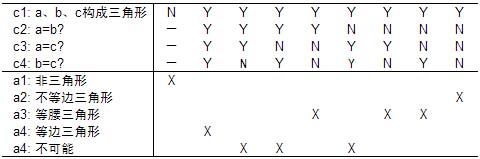
创建决策表需要验证规则的完整性、去冗余、解决不一致性规则
几种功能性测试方法的比较

图片来自Cai Ferriday: A Review Paper on Decision Table-Based Testing
边界值分析法的测试用例数量最多(冗余最多),最容易确定测试用例;基于决策表的测试用例最少,却最难确定测试用例
结构性测试 Structural Testing
1. 路径测试
DD路径 DD-Path(Decision-to-Decision Path)
命令式程序语言可以使用有向图论来分析。将程序语句、语句片断作为节点,控制流作为有向边,就构成了程序有向图
DD-路径: 主要着眼测试覆盖率问题。程序有向图中存在分支,覆盖率考虑的是对各个分支情况的测试覆盖程度,因此对有向图中线性串行的部分进行压缩,在压缩图(即DD-路径)的基础上进行测试用例设计,用测试覆盖指标考察测试效果
例如下面图示的有向图:

对应的DD-Path为:
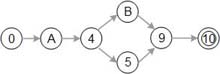
即将节点1,2,3合并成节点A,节点6,7,8合并成节点B
合并原则为: 将一系列邻接的内度=1, 外度=1的节点合并
这样压缩的目的是将程序执行的分支情况清晰的提取出来,便于覆盖率的分析
E. F. Miller指标(覆盖率指标)
C0:所有语句(全节点)
C1:所有的DD-路径(判断分支)(全边)
C1p:所有判断的每种分支
C2:C1覆盖+循环覆盖
Cd:C1覆盖+DD路径的所有依赖对偶
CMCC:多条件覆盖
CiK:包含最多k次循环的所有程序路径(通常k=2)
Cstat:路径具有"统计重要性"的部分.
C无穷:所有可能执行的路径(全路径)
常用的最低指标是C0和C1,这两个指标指明了一个测试的下限。E. F. Miller发现,当一组测试用例满足DD-路径覆盖要求时,大致可以发现全部缺陷的85%
基路径测试 Basis Path Testing
DD-路径只是将程序有向图进行压缩精简,对于简单的DD-路径,我们直观上就可以简单的判断出测试用例的覆盖情况,而对于复杂的控制流则无能为力
Thomas J. McCabe在20世纪70年代进行了深入研究。基路径测试借鉴向量空间中基向量的概念,力图从复杂的控制流中找出一个基路径集合,任何复杂的执行路径都是与这些基路径相关的,虽然对基路径集合的测试覆盖并不能表明对整个应用程序的充分测试,McCabe的研究成果仍带来了重要意义,例如基路径集至少标识了一个最小测试集,对圈复杂度的认可以及开发过程中的检查控制等
图论的一些基本概念
连通分量(connected component): 无向图(undirected graph)中的最大连通子图叫做一个连通分量,例如下图中的连通分量为3

定义及图片均来自wikipedia: Connected component
强连通分量(strongly connected component): 如果有向图(derected graph)中任意一个节点都存在到达其它每个节点的路径,该有向图就是强连通(strongly connected)的。有向图的强连通分量即有向图中最大强连通子图的集合,例如下图的有向图中,用背景标明出了强连通分量
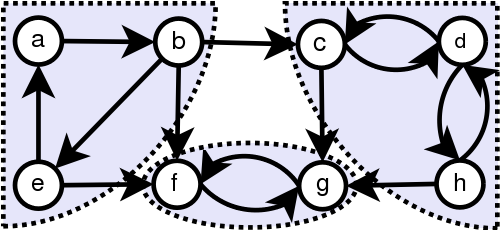
定义及图片均来自wikipedia: Strongly connected component
线性独立路径(linearly independent path): 指程序的一个执行路径(即有向图中初始节点到终止节点的一条路径),并且至少拥有一条以上其它线性独立路径中没有的边。该定义来自Rajib Mall: Fundamentals of Software Engineering
圈复杂度(cyclomatic complexity): M = E − N + 2P
E: 边的数量
N: 节点的数量
P: 连通分量的数量
圈数(cyclomatic number): M = E − N + P
E,N,P参数同上
圈复杂度和圈数之间的关系为:
对有向图A,将A的每个出口(exit)与相应的入口(entrance)相连得到有向图B,则A的圈复杂度与B的圈数相等
圈复杂度又叫做CC复杂度,也可能被称为循环复杂度,它表达的是if .. then .. else .., swith .. case .., 循环语句等分支语句造成的程序控制流复杂程度
例如下图示例一个单入口、单出口的程序图(不是结构化程序图),其圈复杂度为10-7+2=5:

从节点G到A添加一条有向边,则成为一个强连通有向图(该方法对其它结构化程序图同样适用),其圈数为11-7+1=5,与上图的圈复杂度相同:

图2的圈数5就是其线性独立环数量,去掉添加的那条边,也就是图1的线性独立路径数量。这个线性独立路径即对应程序的基路径数量,例如这个示例的5个基路径分别为:
p1: A, B, C, G
p2: A, B, C, B, C, G
p3: A, B, E, F, G
p4: A, D, E, F, G
p5: A, D, F, G
在这个基础上,结合向量空间的运算特性,McCabe开发了Baseline Method用来确定基路径集合,这个基路径集合即可作为测试依据
功能性测试存在冗余,并且忽略了代码实现,存在漏洞;而结构性测试的路径测试方法则忽略了可行路径和不可行路径的差别,在另一个方向上走得太远。数据流测试则部分意义上弥补了这两种测试方法的缺陷
2. 数据流测试
数据流测试与数据流图之间并没有什么关系,数据流测试指关注变量赋值与使用位置的结构性测试方法,可以把它看作是基于路径测试的一种改良方案,一方面仍会使用到路径测试的一些研究成果,另一方面也考虑向功能性测试目标靠近
定义-使用测试 Define-Use Testing
其实在调试修改bug时,我们也会经常这样做,例如在一段代码中搜索某个变量所有的定义、使用位置,思考在程序运行时该变量的值会如何变化,从而分析bug产生原因。这里将这种方法形式化,这样也便于构造算法,实现自动化分析
下面的定义中,P代表程序,G(P)为程序图,V为变量集合,P的所有路径集合为PATH(P)
节点n是变量v的定义节点(变量赋值语句),记做DEF(v,n)
节点n是变量v的使用节点,记做USE(v,n)。如果USE(v,n)是一个谓词使用(条件判断语句中)则记做P-use,如果USE(v,n)是一个运算使用(计算表达式中)则记做C-use
变量v的定义-使用路径记做du-path,如果PATH(P)中的某个路径,如果定义节点DEF(v,m)为该路径的起始节点,使用节点USE(v,n)为该路径的终止节点,则该路径是v的定义-使用路径
变量v的定义-清除路径(define-clear path)记做dc-path,如果变量v的某个定义-使用路径,除了起始节点之外没有其它定义节点,则该路径是变量v的定义-清除路径
结合程序图,找出所有变量的定义-使用路径,考察测试用例对这些路径的覆盖程度,就可以作为衡量测试效果的参考
下面是Rapps-Weyuker数据流覆盖指标的层次结构
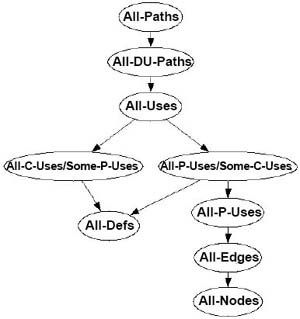
Paul C. Jorgensen: Software Testing - A Craftsman's Approach