原题说明:给定一个 n × n 的二维矩阵表示一个图像。将图像顺时针旋转 90 度。【注:你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。】
原题链接:https://leetcode-cn.com/problems/rotate-image
题目分析:
原地旋转图像,即要求找到某种规律,使得被旋转的元素A(坐标$[i,j]$)经过一系列的操作到与新的坐标$[h,k]$上的元素B发生交换。
所以题目的关键即找到这样的规律。
如图1,首先看到最外圈应该是左上→右上,右上→右下,右下→左下,左下→左上。

所以对图1最外层元素进行分块,见图2

由于左上元素要移动到右上,相对应的、也要将红色色块中的元素移动到黄色色块。依次类推,分别是蓝色块到红色块,绿色块到蓝色块,以及黄色块到绿色块。于是找到每个色块内,元素之间的相同点和不同点,如图3所示。

以红色块的元素移动到黄色块的位置为例,找到就是要红色块中的变化值域映射到黄色块中的变化值域的规律。
设矩阵行元素索引为$i$,列元素索引为$j$。将行元素索引作为外层循环变量,列元素索引为每个色块的移动。换句话说,就是在矩阵的一圈层中,固定$i$不动,通过移动$j$来实现色块间的移动。其变化过程如图4所示

考察上述的过程在所有色块中的变化,于是得到规律如图5所示

四个色块元素转化的规律就是每次列元素索引$j$循环时的不定式。
然后再来处理循环的边界条件。先确定内层循环(列索引$j$)的边界条件,通过分析$n=3,4,5$的情况,了解列索引的边界情况,如图6
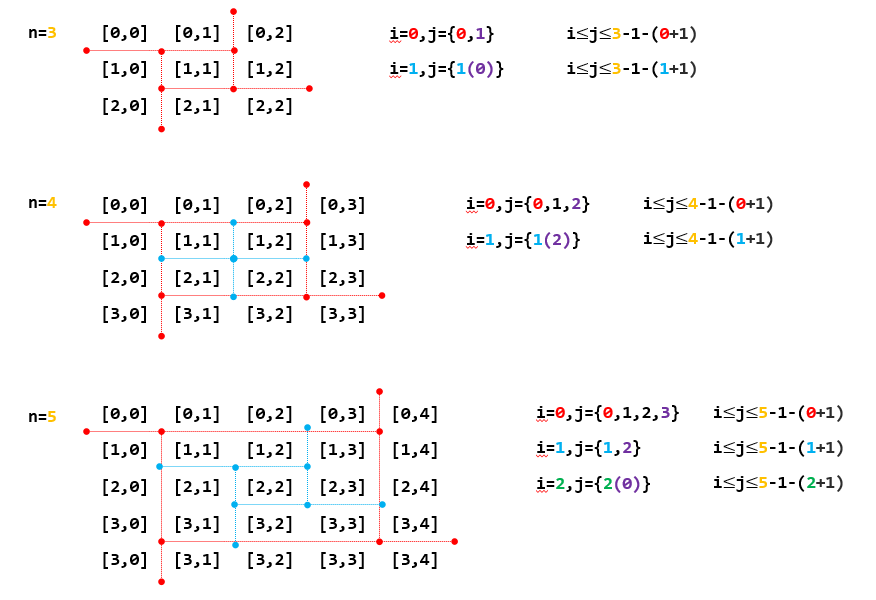
通过对每个图像的肢解,可以看到$j$的初值(每次旋转的起始点)和$i$值一致【其实此处更直观的理解是,进入到下一圈图像时,索引要减去上一圈】,故确定$j$的初值为$i$。对于$n=3$和$n=5$(奇数阶图像)而言,最后一次旋转只有一个中心,故不对此进行操作。由此得到内循环的终止条件为$i leq j leq n-1-(i+1)$,其中$n$为阶数,减$1$是考虑到数组的索引从0开始计数,再减去$i+1$是减去下一个循环边角上的元素(如$[0,4]$和$[1,3]$)、其中的$1$是因为$i$的索引是从0开始计数。
再考虑外层循环的边界条件。由于一次外循环就是图像的一圈,因此要一次减去2行,故终止条件为$i<(n+1) / 2$,加$1$是因为Java的除法遇到整型数据向下取整。
综上所述,得到最后的代码为
1 static void rotate2(int[][] matrix) { 2 if(matrix.length ==0 || matrix == null) 3 return; 4 5 int n = matrix.length; 6 for(int i = 0; i < (n+1)/2; i++) { 7 for(int j = i; j <= n-1-(i+1); j++) { 8 int tmp = matrix[i][j]; 9 10 matrix[i][j] = matrix[n-j-1][i]; 11 matrix[n-j-1][i] = matrix[n-i-1][n-j-1]; 12 matrix[n-i-1][n-j-1] = matrix[j][n-i-1]; 13 matrix[j][n-i-1] = tmp; 14 } 15 } 16 }
总结:
- 作图,用实例化的方法具象化题域,再从中找到解域
- 要多构建相关关系。一开始看的时候,会觉得$j$就只是列的索引值,但是通过寻找关系,发现其也可以作为行索引$j$、如黄色色块(当然,为了方便起见,都是用红色色块举例的),如果只是固定思维,就不容易想到这样的关系。