第十六场快乐数学赛

是不是写模板题写多了？那我们来写点简单的数学吧(^_^) 今天没有任何板子题哦，希望大家开心AC

-- hah,学长也太可耐了

题目难度预估： 简单：A/E/F 中等：D 困难：B/C (然后果真就只写出了简单题)

A - AAA

CodeForces - 359B

int main() {
    // freopen("in.txt","r",stdin);
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n >> k;
    if (k == 0) {
        for (int i = 2; i <= 2 * n; i += 2) cout << i << " " << i - 1 << " ";
        cout << endl;
    } else {
        for (int i = k * 2; i > 0; i--) cout << i << " ";
        for (int i = k * 2 + 1; i <= 2 * n; ++i) cout << i << " ";
    }
}

B. 黑板上的博弈

链接：https://www.51nod.com/Challenge/Problem.html#problemId=1661

第一次做这个平台的博弈（有点难）

Alice和Bob在黑板上玩一个游戏，黑板上写了n个正整数a1, a2, ..., an，游戏的规则是这样的：

1. Alice占有先手主动权。
2. 每个人可以选取一个大于1的数字擦去，并写上一个更小的数字，数字必须是整数，然后由对方进行下一次操作。
3. 如果擦去的数字是 x (x > 1) ，则写上的数字不能比 x/k 小，但是要比 x 小。这里的除法为有理数除法。
4. 不可以擦去任何一个数字 1 ，如果当前无法找到一个数字进行操作，则当前方输。
   假设Alice和Bob都会选择最优的策略，请问Alice是否存在必胜的方案？

输入

第一行两个空格隔开的正整数n和k，其中n表示数字的个数，k表示游戏的参数。
第二行n个空格隔开的正整数，其中第i个表示ai。
1 ≤ n ≤ 10^5, 2 ≤ k ≤ 10^18, 1 ≤ ai ≤ 10^18。

输出

如果存在必胜方案，则输出“Alice i y”，其中i和y表示先手的一种能必胜的操作：将第i个数修改为y。
如果没有，则输出“Bob”表示后手必胜。
（输出不含引号）

这道博弈类似SG函数的变种，太久没写SG都忘记了2333

放一下学长的思路吧

写的时候，只需预处理一下sg值，然后枚举每一位根据sg值来逆推符合条件的x即可。

//待补

C - CCC

CodeForces - 1089F 似乎是2018年的ICPC签到题？

思路指导来自sjy学长：尝试推导一下，假设存在两个数 (frac{x}{a} + frac{y}{c} = frac{bx + ay}{ab} = frac{n - 1}{n})

那么可得 (a * b = n)，则可以枚举 (n) 的因子，然后得到 b，因为是分数，需要再枚举(x) 来计算 (y)

// Author : RioTian
// Time : 20/11/03
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n;
int main() {
    // freopen("in.txt","r",stdin);
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n;
    for (ll i = 2; i <= sqrt(n); ++i) {
        if (n % i == 0)  //枚举因子
            for (ll j = 1; j < i; j++)
                if ((n - 1 - j * n / i) % i == 0) {
                    printf("YES
2
%lld %lld
%lld %lld
", j, i,
                           (n - 1 - j * n / i) / i, n / i);  //只需要两个即可
                    return 0;
                }
    }
    cout << "NO
";
}

D - DDD

LibreOJ - 538 题面太长、完全没看

容易发现数列最后一定单调，最后单调递增则最大值赋为最后一个，反之最小值赋为最后一个，然后处理一些细节就可以AC，要注意以下几点：

1.数列连续三项以及数列最后一项 (>10^7)时退出。

2.可能第一要求项就比你枚举的大，需要特判。

3.要求项的枚举不能等于最大项，不然会无法正常指向最后一个。

// Author : RioTian
// Time : 20/11/03
#include <bits/stdc++.h>
#define ll long long
#define lowbit(x) x & -x
using namespace std;
int read() {
    char c;
    int s = 0, t = 1;
    while (!isdigit(c = getchar()))
        if (c == '-') t = -1;
    do {
        s = s * 10 + c - '0';
    } while (isdigit(c = getchar()));
    return s * t;
}
const int inf = 0x3f3f3f3f, maxn = 500010;
const ll MAXS = 1e15;

int n, m, k, s[maxn];
ll a[maxn];
int main() {
    //    freopen("seq8.in","r",stdin);
    //    freopen("hi.out","w",stdout);
    int mx = 0;
    m = read();
    for (int i = 1; i <= m; i++) s[i] = read(), mx = max(s[i], mx);
    n = read();
    int N = min(90, mx);
    for (int i = 1; i <= n; i++) {
        int now = N;
        a[0] = read();
        a[1] = read();
        k = read();
        for (int j = 2; j <= N; j++) {
            a[j] = 1ll * k * a[j - 1] + a[j - 2];
            if ((a[j] >= 0 && a[j - 1] >= 0 && a[j - 2] >= 0 && a[j] > MAXS) ||
                (a[j] <= 0 && a[j - 1] <= 0 && a[j - 2] <= 0 && a[j] < -MAXS)) {
                now = j;
                break;
            }
        }
        ll mins = 1ll << 60, maxs = -(1ll << 60);
        int maxi = -1, mini = -1;
        for (int j = 1; j <= m; j++)
            if (s[j] < now) {
                if (a[s[j]] > maxs) maxs = a[s[j]], maxi = s[j];
                if (a[s[j]] < mins) mins = a[s[j]], mini = s[j];
            } else
                break;
        if (maxi == -1) maxi = s[1];
        if (mini == -1) mini = s[1];
        if (a[now] > 0 && a[now] > maxs) maxi = mx;
        if (a[now] < 0 && a[now] < mins) mini = mx;
        printf("%d %d
", maxi, mini);
    }
    return 0;
}

E - EEE

AtCoder - abc174_e

挺好的二分解题套路：二分每个长度即可

// Author : RioTian
// Time : 20/11/03
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 10;
int a[N], n, k;
bool check(int x) {
    int res = 0;
    for (int i = 0; i < n; i++) {
        if (a[i] > x) {
            res += a[i] / x;
            if (a[i] % x == 0) res--;
        }
    }
    return res <= k;
}
int main() {
    // freopen("in.txt", "r", stdin);
    // ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    cin >> n >> k;
    for (int i = 0; i < n; i++) cin >> a[i];
    int l = 1, r = 1e9;
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid))
            r = mid;
        else
            l = mid + 1;
    }
    cout << l << endl;
}

F - FFF

AtCoder - abc174_d

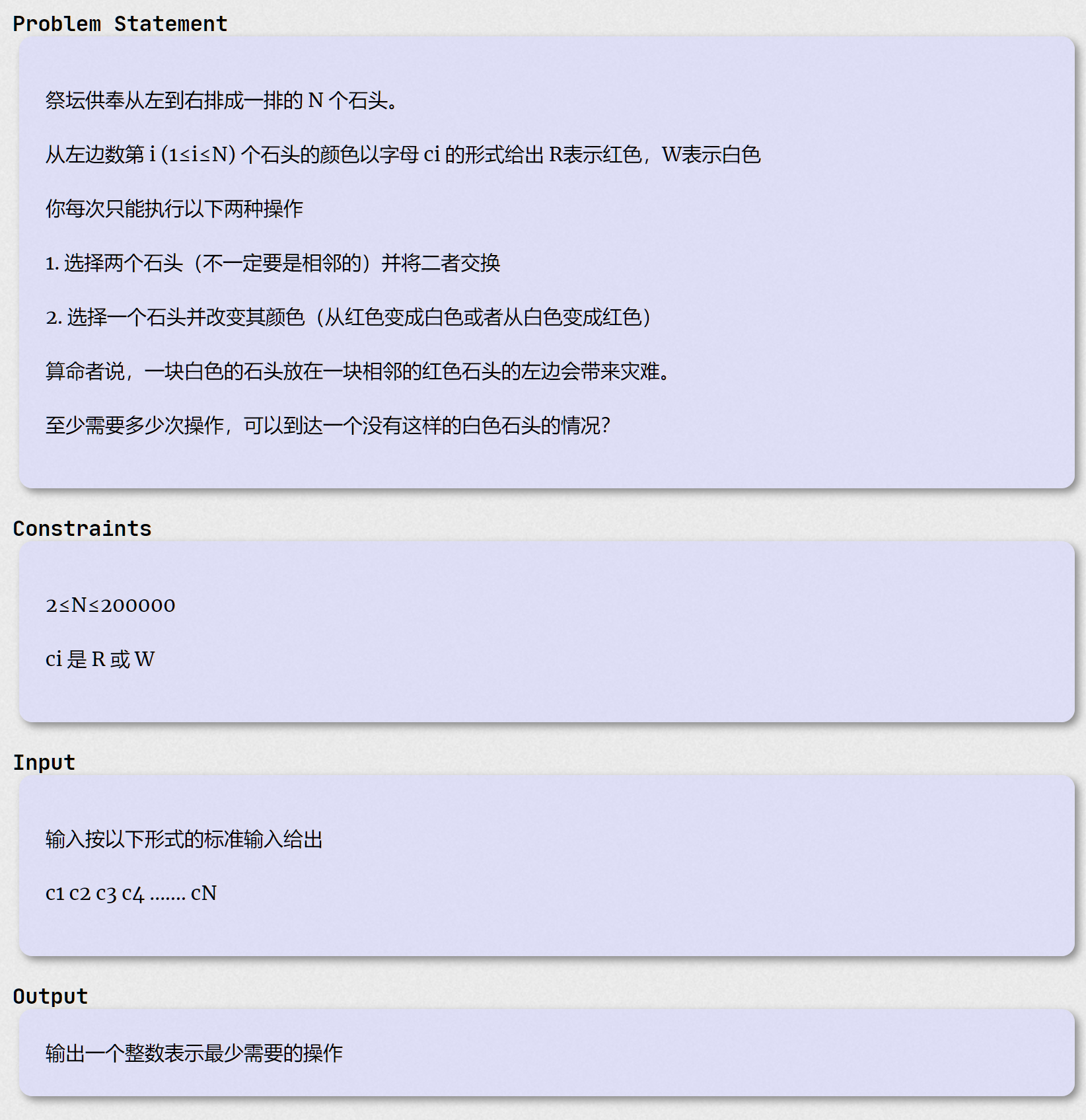
思路：统计所有 R 的数量 num，这些 R 都可以通过一操作移到最左边， 那么只要查询 [0,num] 的范围里有多少个 W 需要交换即可。

//优化以后的写法
int main() {
    cin >> n >> s;
    cout << count(s.begin(), s.begin() + count(s.begin(), s.end(), 'R'), 'W');
}

int main() {
    cin >> n >> s;
    int i = 0, j = n - 1, cnt = 0;
    while (i < j) {
        while (s[i] == 'R' && i < j) i++;
        while (s[j] == 'W' && j > i) j--;
        if (s[i] != s[j]) cnt++;
        i++, j--;
    }
    cout << cnt << endl;
}