一些 Codeforce Content 补题记录

Codeforces Round #651 (Div. 2)

1370A. Maximum GCD

给定一个 n，求（1~n）中任意组合对的最大的公约数。

思路：如果 (n) 是偶数，那么最大公约数为 $ n / 2$ ，反之 为 ((n - 1) / 2)。但由于C++ int类型在进行除法时会向下取整所以：cout << n / 2 << endl;

void solve() {
    int n;
    cin >> n;
    cout << n / 2 << endl;
}

1370B. GCD Compression

题目大意：给定包含元素个数为2n的数组a,删去其中2个元素，剩下的元素两两组合求和，构成包含n-1个元素的数组b,要求数组b中的元素共有的因子大于1,输出数组a两两选择数据所处的位置.

基本思路：数组a中元素数值的构成要么奇数，要么偶数，考虑到奇数+奇数=偶数,偶数+偶数=偶数,可以构造出和值为偶数的n-1个数，这样，共有因子是2.

AC代码

void solve() {
    int n;
    cin >> n;
    n = 2 * n;
    vector<int> a(n), b[2];
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        b[a[i] % 2].push_back(i);
    }
    vector<pair<int, int> > ans;
    for (int j = 0; j < 2; j++) {
        while (b[j].size() > 1)
            ans.push_back({b[j][b[j].size() - 1], b[j][b[j].size() - 2]}),
                b[j].pop_back(), b[j].pop_back();
    }
    while (ans.size() > n / 2 - 1) ans.pop_back();
    for (auto it : ans) cout << it.first + 1 << " " << it.second + 1 << endl;
}

1370C. Number Game

题目大意：给定一个数 (n),当前操作者，可以在一下两个操作中任选一个:

1. 若 (n) 能整除奇数，并且能保证整除奇数后的结果大于1,可以考虑让 (n) 整除奇数，整除后的结果更新n，参与接下的操作。

2. 若 (n-1) 的结果大于1,可以考虑让 (n-1) 的结果更新 (n)，参与接下的操作。

若当前操作者，什么操作也做不了，那么当前操作者认输。

输出该次比赛的获胜者。

样例模

Ashishgup(简写为A),FastestFinger(简写为F)
 
1
FastestFinger
 
n=1,轮到A什么都做不了，F赢
 
 
2
Ashishgup
 
n=2,轮到A,n=2-1=1
n=1,轮到F什么都做不了，A赢
 
3
Ashishgup
 
n=3,轮到A,n=3/3=1
n=1,轮到F什么都做不了，A赢
 
4
FastestFinger
 
n=4,轮到A,n=4-1=3
n=3,轮到F,n=3/3=1
n=1,轮到A什么都做不了，F赢
 
5
Ashishgup
 
n=5,轮到A,n=5/5=1
n=1,轮到F什么都做不了，A赢
 
6
FastestFinger
 
n=2*3,轮到A,n=2*3/3=2
n=2,轮到F,n=2-1=1
n=1,轮到A什么都做不了，F赢
 
 
12
Ashishgup
 
n=2*2*3,轮到A,n=2*2*3/3=2*2
n=2*2,轮到F,n=2*2/2=2
n=2,轮到A,n=2-2=1
n=1,轮到F什么都做不了，A赢

只靠样例这点数据，该题是难以AC的，继续举例如下

1. 下面是因式分解，只有偶数因子的情况

Ashishgup(简写为A),FastestFinger(简写为F)
 
8
FastestFinger
 
n=8=2*2*2,轮到A,n=8-1=7
n=7,轮到F,n=8/7=1
n=1,轮到A什么都做不了，F赢
 
上面是因式分解，没有奇数因子的情况

2. 有偶数因子(偶数因子的个数大于等于2)，同时也有奇数因子

Ashishgup(简写为A),FastestFinger(简写为F)
 
12
Ashishgup
 
n=12=2*2*3,轮到A,n=2*2*3/3=2*2
n=2*2,轮到F,n=4-1=3
n=3,轮到A,n=3/3=1
n=1,轮到F什么都做不了，A赢
 
 
120
Ashishgup
 
n=120=2*2*2*3*5,轮到A,n=2*2*2*3*5/(3*5)=2*2*2,注意，将奇数因子一次耗尽
n=2*2*2,轮到F,n=8-1=7
n=7,轮到A,n=7/7=1
n=1,轮到F什么都做不了，A赢

3. 有偶数因子(偶数因子的个数等于1)，同时也有奇数因子

Ashishgup(简写为A),FastestFinger(简写为F)
 
只有一个奇数因子
6
FastestFinger
 
n=6=2*3,轮到A,n=2*3/3=2
n=2,轮到F,n=2-1=1
n=1,轮到A什么都做不了，F赢
 
奇数因子个数大于等于2
30
Ashishgup
 
n=30=2*3*5,轮到A,n=2*3*5/5=2*3
n=2*3,轮到F,n=2*3/3=2
n=2,轮到A,n=2-1=1
n=1,轮到F什么都做不了，A赢
 
 
奇数因子个数大于等于2
90
Ashishgup
 
n=90=2*3*3*5,轮到A,n=2*3*3*5/(3*5)=2*3
n=2*3,轮到F,n=2*3/3=2
n=2,轮到A,n=2-1=1
n=1,轮到F什么都做不了，A赢

AC Code 1

string name[2] = {"Ashishgup
", "FastestFinger
"};
void solve() {
    ll n;
    cin >> n;
    // 特判 n == 1 和 n == 2
    if (n == 1)
        cout << name[1];
    else if (n == 2 || n % 2)
        cout << name[0];
    else {
        int cnt0 = 0, cnt1 = 0;  // 统计偶数因子和奇数因子的个数
        // 质因数分解
        for (int i = 2; i * i <= n; ++i) {
            if (n % i == 0)
                while (n % i == 0) {
                    n /= i;
                    if (i == 2)
                        cnt0++;
                    else
                        cnt1++;
                }
        }
        if (n > 1) cnt1++;
        if (cnt1 == 0)
            cout << name[1];  //只有偶数因子
        else if (cnt0 >= 2)
            cout << name
                    [0];  //有偶数因子(偶数因子的个数大于等于2)，同时也有奇数因子
        else if (cnt0 ==
                 1) {  //有偶数因子(偶数因子的个数等于1)，同时也有奇数因子
            if (cnt1 == 1)
                cout << name[1];  //奇数因子个数是1
            else
                cout << name[0];  //奇数因子个数大于等于2
        }
    }
}

AC Code 2

把上面的思路转换一下就是下方的 ↓

FastestFinger赢的条件 $n = (1，)n = 2^x$，其中（x> 1）和 (n =2⋅p) ，其中 (p) 是大于3的素数，否则Ashishgup获胜。

// 素数判定
bool check_prime(int n) {
    for (int i = 2; i < min(N, n); i++)
        if (n % i == 0) return 0;
    return 1;
}

void solve() {
    ll n;
    cin >> n;
    bool lose = (n == 1);
    if (n > 2 && n % 2 == 0) {
        if ((n & (n - 1)) == 0)
            lose = 1;
        else if (n % 4 != 0 && check_prime(n / 2))
            lose = 1;
    }
    cout << (!lose ? "Ashishgup" : "FastestFinger") << endl;
}

1370D. Odd-Even Subsequence

二分或者DP

思路：对答案进行二进制搜索并检查是否给定 x，则有可能形成长度至少为 k 的子序列，以使所有处于奇数索引或偶数索引的元素均 ≤x。

const int N = 2e5 + 5;

int a[N], n, k;
bool check(int x, int cur) {
    int ans = 0;
    for (int i = 1; i <= n; ++i) {
        if (!cur)
            ans++, cur ^= 1;
        else if (a[i] <= x)
            ans++, cur ^= 1;
    }
    return ans >= k;
}

int binsearch(int lo, int hi) {
    while (lo < hi) {
        int mid = (lo + hi) / 2;
        if (check(mid, 0) || check(mid, 1))
            hi = mid;
        else
            lo = mid + 1;
    }
    return lo;
}

void solve() {
    cin >> n >> k;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    cout << binsearch(1, 1e9) << endl;
}

Codeforces Round #652 (Div. 2)

1369A.FashionabLee 正多边形

题目大意：给定一个正多边形，放置于平面直角坐标系的第一象限，若能做到一条边与x轴平行的同时，另一条边能与y轴平行的同时,输出YES,否则输出NO。

简单画下图就可以发现，当边数为4的倍数时即符合条件

void solve() {
    ll n; cin >> n;
    cout << (n % 4 == 0 ? "YES" : "NO") << endl;
}

1369B. AccurateLee

如果字符串s是非递减的，则答案是s本身，否则答案是x+1个零和y个1，其中x是字符串s的前导零个数，y是字符串s的尾随零个数。

void solve() {
    ll n;
    string s;
    cin >> n >> s;
    bool flag = true;
    for (int i = 1; i < s.size(); i++) {
        if (s[i] < s[i - 1]) flag = 0;
    }
    if (flag) {
        cout << s << endl;
        return;
    }
    string ans;
    for (int i = 0; i < n; ++i) {
        if (s[i] == '1') break;
        ans.push_back('0');
    }
    ans.push_back('0');
    for (int i = n - 1; i >= 0; --i) {
        if (s[i] == '0') break;
        ans.push_back('1');
    }
    cout << ans << endl;
}

1369C. RationalLee

const int N = 2e5 + 10;

vector<int> v[N];
void solve() {
    ll n, k;
    cin >> n >> k;
    ll a[n], w[k];

    for (int i = 0; i <= n; ++i) v[i].clear();

    for (int i = 0; i < n; ++i) cin >> a[i];
    for (int i = 0; i < k; ++i) cin >> w[i];

    sort(a, a + n), sort(w, w + k);

    for (int i = 0; i < k / 2; ++i) swap(w[i], w[k - i - 1]);

    ll po = 0, ans = 0;
    for (int i = 0; i < n; ++i) {
        while (w[po] == v[po].size() + 1) po++;
        v[po].push_back(a[i]);
    }

    int cnt = 1;
    for (int i = 0; i < k; ++i) {
        ans += a[n - i - 1];
        if (v[i].size())
            ans += v[i][0];
        else
            ans += a[n - cnt++];
    }
    cout << ans << endl;
}

//46ms 解法
void solve() {
    ll n, k;
    cin >> n >> k;
    ll a[n], w[k];

    for (int i = 0; i <= n; ++i) v[i].clear();

    for (int i = 0; i < n; ++i) cin >> a[i];
    for (int i = 0; i < k; ++i) cin >> w[i];

    sort(a, a + n), sort(w, w + k);
    ll ans = 0;
    for (int i = n - 1; i >= n - k; --i) ans += a[i];

    int i = n - k, j = 0, t = n - 1;
    while (j < k) {
        if ((w[j]--) == 1)
            ans += a[t];
        else
            ans += a[i -= w[j]];
        j++, t--;
    }
    cout << ans << endl;
}

1369D. TediousLee (DP)

题意

最初有一个结点，衍生规则如下：

• 如果结点 u 没有子结点，添加 1 个子结点
• 如果结点 u 有 1 个子结点，添加 2 个子结点
• 如果结点 u 有 3 个子结点，跳过该结点

如：

[level=1,2,3,4 ]

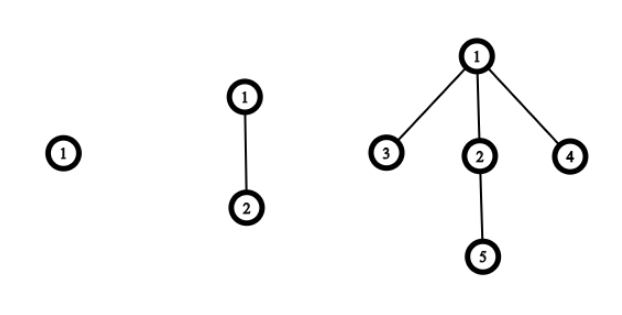
爪形结构如下：

问可以在 levelnleveln 选出几个互不相交的爪形结构。

Key idea

衍生的过程是具有重复性的，最终变化的是根结点 (1) 下的三棵子树，左右两棵子树为 (level_{n−2})，中间的子树为 (level_{n−1}) 。

因为 (level_{1}) 和 (level_{2}) 的根节点并未使用，所以可以在(level_{3}) 中选择根节点 (1) 为中心的爪形结构

同理，(level_{4})、(level_{5}) 可以通过选取较下层的爪形结构来避免根结点的使用，所以在 (level_{6}) 中又可以选取以根结点 (1) 为中心的爪形结构。

即，(level_{1}) 为 (3) 的倍数的图形都可以再额外选取位于根结点的爪形结构。

综上，设 (dp_i) 为 (level_{i}) 中最多可选出的互不相交的爪形结构个数，有递推式：

[dp_i = 2 *dp_{i - 2} + dp_{i - 1} + (i \% 3 == 0) ]

const int N = 2e6 + 10;
const int mod = 1e9 + 7;
int _;
int dp[N];
void init() {
    dp[1] = dp[2] = 0;
    dp[3] = dp[4] = 1;
    for (int i = 5; i < N; ++i)
        dp[i] = (2LL * dp[i - 2] + dp[i - 1] + (i % 3 == 0)) % mod;
}
void solve() {
    int n;
    cin >> n;
    cout << 4LL * dp[n] % mod << endl;
}
int main() {
    // freopen("in.txt", "r", stdin);
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    init();
    for (cin >> _; _--;) solve();
}

Educational Codeforces Round 90 (Rated for Div. 2)

1373A. Donut Shops

题意

有两种包装的甜甜圈，第一种 1 个 a 元，第二种 b 个 c 元，问买多少个甜甜圈按第一种买会更便宜，买多少个甜甜圈按第二种买会更便宜，输出任一方案。

题解

梳理过后发现本题只需回答两个问题：

1. 要不要买第一种包装
2. 要不要买第二种包装

第一种包装是要买 1 个，花费 a 元，若买第二种替代，最少要买 b 个，花费 c 元，所以比较 a 和 c 。

同理，第二种包装要买 b 个，花费 c 元，若买第一种替代，最少要买 b 个，花费 (a×b) 元，所以比较 c 和 $a×b $。

void solve() {
    ll a, b, c;
    cin >> a >> b >> c;
    cout << (a < c ? 1 : -1) << " " << (c < a * b ? b : -1) << endl;
}

1373B.01 Game（字符串博弈）

题意

给出一个二进制串 (s)，Alica 和 Bob 每次可以选择移去 (s) 中的一个 (10) 或 (01)，无法选择者视为输掉游戏，判断最终谁会胜利。（(1≤t≤1000,1≤|s|≤100)）

方法一：

(|s|) 较小，直径模拟即可，(O(n^2))

void solve() {
    string s;
    cin >> s;
    int ans = 0;
    bool flag = false;
    while (1) {
        bool flag = false;
        for (int i = 0; i + 1 < s.size(); i++) {
            if (s[i] != s[i + 1]) {
                s = s.substr(0, i) + s.substr(i + 2);
                ++ans;
                flag = true;
            }
        }
        if (!flag) break;
    }
    cout << (ans & 1 ? "DA" : "NET") << "
";
}

方法二

进一步观察发现在移除所有相邻的不同字符后，字符串最终为连续的 (0) 或 (1)，即移除了 (0) 和 (1) 中的较少者，其个数代表着游戏总共可以进行多少步，然后奇偶判断即可、

void solve() {
    string s;
    cin >> s;
    int cnt[2] = {};
    for (char c : s) ++cnt[c - '0'];
    int mi = min(cnt[0], cnt[1]);
    cout << (mi & 1 ? "DA
" : "NET
");
}

1373C. Pluses and Minuses（差分）

题意

给出一个只含有 (+) 或 (−) 的字符串 (s)，按如下伪代码进行操作

res = 0
for init = 0 to inf
    cur = init
    ok = true
    for i = 1 to |s|
        res = res + 1
        if s[i] == '+'
            cur = cur + 1
        else
            cur = cur - 1
        if cur < 0
            ok = false
            break
    if ok
        break

计算最终 (res) 的值。

题解

(res) 即所有位置被访问次数的总和。

模拟伪代码，计算走到每个位置时的值，如果当前位置的值比之前所有位置的都要小，则此时 (cur<0)，意味着当前位置及之前的字符都要再走一遍，而且下一次走到当前位置时 (cur=0) 。

//或许更好理解的差分写法。
void solve() {
    string s;
    cin >> s;
    ll ans = s.size();
    int mi = 0, now = 0;
    for (int i = 0; i < s.size(); i++) {
        if (s[i] == '+')
            ++now;
        else
            --now;
        if (now < mi) {
            mi = now;
            ans += i + 1;
        }
    }
    cout << ans << "
";
}

1373D. Maximum Sum on Even Positions（dp）

题意

给出一个大小为 (n) 的数组 (a)，下标为 (0∼n−1)，可以进行一次反转一个区间中元素的操作，问偶数下标元素的最大和，

题解

如果反转区间长度为奇数，则下标奇偶性不同的元素间不会互换，所以反转的区间长度为偶数，反转后的区间可以看作相邻元素两两交换所得。

如：1 2 3 4 反转后为 4 3 2 1，偶数下标元素由 1 3 变成了 2 4 ，可以看作 1 与 2 相交换，3 与 4 相交换。

枚举反转区间左端点的奇偶性：

• 左端点为偶数，对于每个子区间 [i, i + 1]，反转后的收益为 (a_{i+1}−a_i)
• 左端点为奇数，对于每个子区间 [i, i + 1]，反转后的收益为 (a_i−a_{i+1})

所需反转的总区间即为加起来收益最大的一些连续子区间。

void solve() {
    int n;
    cin >> n;
    int a[n] = {};
    for (int i = 0; i < n; i++) cin >> a[i];
    ll mx = 0, al = 0, ar = 0;
    for (int st : {0, 1}) {  //枚举反转区间左端点的奇偶性
        ll sum = 0, l = st, r = st;  // sum 是以当前子区间结尾的最大收益，[l, r]
                                     // 是该最大收益所在的区间
        for (int i = st; i + 1 < n; i += 2) {
            int val = (st == 0 ? a[i + 1] - a[i]
                               : a[i] - a[i + 1]);  //当前子区间的收益
            if (sum > 0) {  //如果之前区间的收益大于0
                sum += val;
                r = i + 1;
            } else {
                sum = val;
                l = i;
                r = i + 1;
            }
            if (sum > mx) {
                mx = sum;
                al = l, ar = r;
            }
        }
    }
    ll ans = 0;
    reverse(a + al, a + ar + 1);
    for (int i = 0; i < n; i += 2) ans += a[i];
    cout << ans << endl;
}

Codeforces Round #654 (Div. 2)

1371A. Magical Sticks

void solve() {
    int n;
    cin >> n;
    cout << (n + 1) / 2 << endl;
}

1371B. Magical Calendar

void solve() {
    ll n, r;
    cin >> n >> r;
    ll k = min(n - 1, r);
    cout << (k + 1) * k / 2 + (r >= n) << endl;
}

1371C. A Cookie for You

题意：给定 (a) 个香草饼干和 (b) 个巧克力饼干，然后有两批客人分别是 (n) 和 (m)个人，选饼干遵循以下两种规则

• 如果第一类客人：如果a > b，客人选择香草饼干。否则，客人会选择巧克力饼干。
• 如果客人是第二种类型：如果a >b，客人选择巧克力饼干。否则，客人会选择香草饼干。

如果两批客人均满足即 输出 YES 否则输出 NO

思路：
首先判断 两种 饼干的数量是否超过 总的 客人数 (a + b >= n + m)，同时只要饼干数少的满足大于第二批客人的数量即可。

void solve() {
    ll a, b, n, m;
    cin >> a >> b >> n >> m;
    cout << (a + b >= n + m and min(a, b) >= m ? "YES
" : "NO
");
}

1371D. Grid-00100

• 1.k%n=0:

  

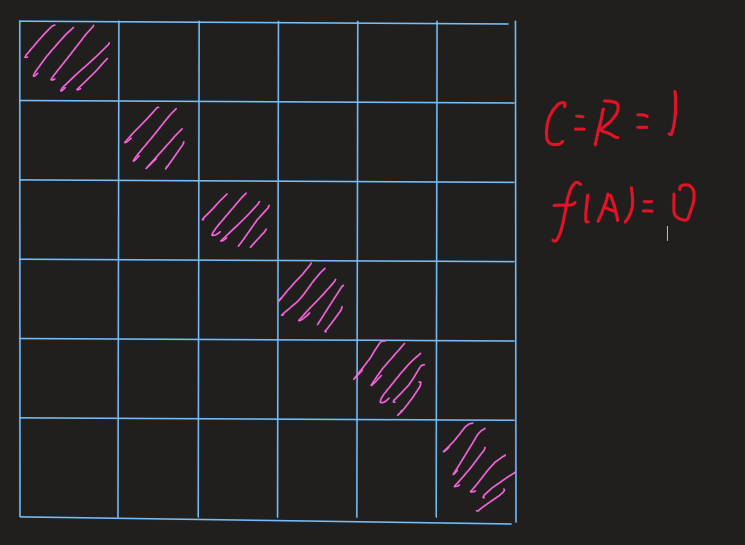
  2.k%n!=0:

  

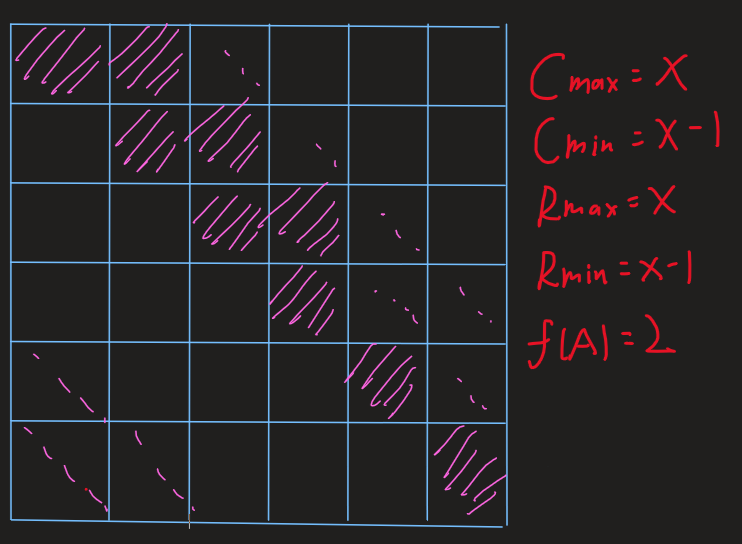
  这样的话,规律应该显而易见了吧,我们沿着对角线构造,然后取余,填填补补即可,具体的看代码吧.

• 代码:

const int maxn = 310;
int A[maxn][maxn];
void solve() {
    ll n, k;
    cin >> n >> k;
    cout << not not(k % n) * 2 << "
";
    for (int i = 0; i < n; i += 1)
        for (int j = 0; j < n; j += 1) A[i][j] = 0;
    for (int i = 0; i < n; i += 1)
        for (int j = 0; j < n; j += 1)
            if (k) {
                A[j][(i + j) % n] = 1;
                k -= 1;
            }
    for (int i = 0; i < n; i += 1) {
        for (int j = 0; j < n; j += 1) cout << A[i][j];
        cout << "
";
    }
}

Codeforces Global Round 9

1375A. Sign Flipping

题意：翻转某些数字，使得数为 (a[i] - a[i - 1] >= 0 or a[i] - a[i - 1]<=0)

题解：首先全转化为正数，然后按奇数位变为负数即可。

void solve() {
    int n;
    cin >> n;
    for (int i = 0, k = 1, x; i < n; ++i, k = -k) {
        cin >> x;
        cout << abs(x) * k << " ";
    }
    cout << endl;
}

1375B. Neighbor Grid

当给定一个二维数组的时候，我们总是能够想办法构造出一个解法，除非某些值超过了限制（因为我们只能不断增加数值）。
比如一个5 x 5 二维数组，它数值最大的解如下：
2 3 3 3 2
3 4 4 4 3
3 4 4 4 3
3 4 4 4 3
2 3 3 3 2

证明：
首先，图中每个数值表示的是当前点的邻居数量，如果比该数量还大，则没有解。

• 假如应该为4的点比4还要大，由于只有四个邻居，所以没有解。
• 假如应该为3的点比3还要大，由于3的点都在边缘，只有三个邻居，所以没有解。
• 假如应该为2的点比2还要大，由于2的点都在角落，只有两个邻居，所有没有解。

其次，这确实是一个合法的解。

则得到解法：

• 假如这个二位数组的每个点的初始数值都不超过这个解，那么我们总是可以通过增加数值的方式得到这个解。
• 如果这个二位数组有的点的初始数值已经超过了这个解，那么我们无法得到一个解答。

int a[310][310];
void solve() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j) cin >> a[i][j];

    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j) {
            int ans = 0;
            if (i > 1) ans += 1;
            if (i < n) ans += 1;
            if (j > 1) ans += 1;
            if (j < m) ans += 1;
            if (ans < a[i][j]) {
                cout << "NO
";
                return;
            }
            a[i][j] = ans;
        }
    cout << "YES
";
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) cout << a[i][j] << " ";
        cout << endl;
    }
}

1375C. Element Extermination

void solve() {
    int n;
    cin >> n;
    int a[n + 1];
    for (int i = 1; i <= n; ++i) cin >> a[i];
    cout << (a[1] < a[n] ? "YES
" : "NO
");
}

1375D. Replace by MEX

由于每次放入的都是MEX，也就是说如果放入了MEX，则这个数不会再成为MEX（除非又被换出来）。

如果我们每次把MEX放到下标为MEX的位置，则我们可以不断把MEX归位。且不会再有同样的值来替换已经归位的数（因为它不再是MEX)。这样我们每次操作可以归位一个数。

但由于一共 (n+1)个数，放入n个位置中，所以最大的那个数n将没有地方放。我们把最大的数放入n-1这个位置中（后来想想其实这步没有必要）。但假如n-1的位置中已经放置了n-1这个数，则我们找到一个没有被归位的位置，把n放进去。下次的MEX一定不是n，于是可以归位一个数。这样我们两次操作可以归位一个数。所以以上解法是可以在2n次操作内解决的。

每次找到MEX同时验证是否是合法解，需要一次遍历。当 (n) 无法放入 (n-1)位置时，会再进行一次遍历。2n次操作则时间复杂度为 (O(n^2))。由于n最大为1000，所以已经可以解决，无需进一步优化。

void solve() {
    int n;
    cin >> n;
    int num[1002];
    for (int i = 0; i < n; i++) cin >> num[i];

    vector<int> seq;
    while (true) {
        vector<int> mask(n + 1);
        bool is_valid = true;
        // 记录哪些数出现过，并验证是否是非下降数组.
        for (int i = 0; i < n; i++) {
            mask[num[i]] = 1;
            if (i > 0)
                if (num[i] < num[i - 1]) is_valid = false;
        }
        if (is_valid) break;

        int mex;
        for (int i = 0; i <= n; i++) {
            if (mask[i] == 0) {
                mex = i;
                break;
            }
        }
        if (mex != n) {
            // 归位
            num[mex] = mex;
            seq.push_back(mex + 1);
        } else {
            if (num[n - 1] == n - 1) {
                // 找到一个还没有归位的位置放进去。
                for (int i = 0; i < n; i++) {
                    if (num[i] != i) {
                        num[i] = mex;
                        seq.push_back(i + 1);
                        break;
                    }
                }
            } else {
                // 直接放入n-1的位置。也可以不要这一步，都放入没有归位的位置。
                num[n - 1] = mex;
                seq.push_back(n);
            }
        }
    }

    cout << seq.size() << endl;
    for (int i = 0; i < seq.size(); i++) cout << seq[i] << " ";
    cout << endl;
}

现在开始是2021年的比赛题目了

Codeforces Round #693 (Div. 3)

1472A. Cards for Friends

void solve(){
    ll w,h,n;
    cin >> w >> h >> n;
    cout << ((w * -h & w * h) < n ? "NO
" : "YES
");
}

1472B. Omkar and Last Class of Math

题意：Alice 和 Bob 分糖果，每包糖果只有 1 或 2 个，请问是否能平分。

思路：统计 1 个 和 2 个的包数，进行奇偶数判断即可。

void solve() {
    int n; cin >> n;
    int cnt[3] = {}, x;
    for (int i = 0; i < n; ++i)  cin >> x, cnt[x]++;
    if (cnt[1] & 1) cout << "NO
";
    else if (cnt[1] == 0 and (cnt[2] & 1)) cout << "NO
";
    else cout << "YES
";
}

1472C. Long Jumps

题意： Polycarp在玩一个游戏，给定有n个元素的数组a，设定一个起始点i。当 i <= n 时， i = i + a[i]，得分score = score + a[i]，试求出对于数组a可以得出的最大得分。

思路：

首先这道题数据量较大，时限2s，暴力求解是肯定⑧行的。

仔细观察题目，对于每一个假定的起始值 i ，分为两种情况：

• i + a[i] > n ，这时其得分 ans = a[i]。

• i + a[i] <= n ，这时游戏并未结束 i = i + a[i] , 得分ans += a[i] ，并进行下一轮，直到i + a[i] > n为止。

  如果我们从 i = n 开始遍历，并将a[i] 的得分储存在 a[i] 中，即使出现 i + a[i] <= n的情况 ,其a[i+a[i]]的得分已经计算好，不需要从头开始计算。

void solve() {
    long long a[N], n, maxn = 0;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = n; i > 0; i--) {
        if (i + a[i] <= n) a[i] += a[i + a[i]];
        if (a[i] > maxn) maxn = a[i];
    }
    cout << maxn << endl;
}

1472D. Even-Odd Game

Alice遇偶数加分否则无操作，Bob遇奇数加分否则无操作。

[(A>B) –> (A-B) >0 ]

排序，依次往下加

void solve() {
    int n;
    cin >> n;
    vector<ll> a(n);
    for (auto& x : a) cin >> x;
    ll Aans = 0, Bans = 0;
    sort(a.begin(), a.end(), greater<ll>());
    for (int i = 0; i < n; ++i) {
        if (i % 2 == 0) {
            if (a[i] % 2 == 0) Aans += a[i];
        } else if (a[i] & 1)
            Bans += a[i];
    }
    if (Aans > Bans)
        cout << "Alice
";
    else if (Aans < Bans)
        cout << "Bob
";
    else
        cout << "Tie
";
}

1472E. Correct Placement

让我们把所有人按身高降序排列。
现在让我们遍历所有人，并在排序数组中查找此人的位置，其高度严格小于我们的高度（例如，通过二进制搜索）。显然，只有那些在排序数组中比找到的人晚的人才能站在我们面前（所有人的身高都比我们的要低）。
在所有这些人中，用最小宽度的人对我们更有利。为了快速找到这样的人，我们可以找到一个人的最小宽度为每个后缀的排序数组。
要处理一个人躺着的情况，我们需要交换宽度和高度，然后重复上面的算法。

这里用了 tuple 元组解决，码量少了很多

void solve() {
    int n;
    cin >> n;
    vector<pair<int, int>> v(n);
    // for (int i = 0; i < n; ++i) cin >> v[i].first >> v[i].second;
    for (auto& [x, y] : v) cin >> x >> y;
    vector<tuple<int, int, int>> vt;
    for (int i = 0; i < n; ++i) {
        vt.push_back({v[i].first, v[i].second, i});
        vt.push_back({v[i].second, v[i].first, i});
    }
    sort(vt.begin(), vt.end());
    vector<tuple<int, int, int>> ok;
    for (auto [x, y, z] : vt) {
        if (ok.empty())
            ok.push_back({x, y, z});
        else {
            auto [_, by, __] = ok.back();
            if (y < by) ok.push_back({x, y, z});
        }
    }
    for (int i = 0; i < n; i += 1) {
        auto it =
            lower_bound(ok.begin(), ok.end(), make_tuple(v[i].first, 0, 0));
        if (it == ok.begin())
            cout << "-1 ";
        else {
            auto [x, y, z] = *prev(it);
            if (y < v[i].second)
                cout << z + 1 << " ";
            else
                cout << "-1 ";
        }
    }
    cout << "
";
}

Codeforces Round #694 (Div. 2)

1471A. Strange Partition

void solve() {
    int n, x;
    cin >> n >> x;
    vector<ll> a(n);
    ll minx = 0, maxx = 0;
    for (auto&& v : a) {
        cin >> v;
        minx += v, maxx += (x + v - 1) / x;
    }
    cout << (minx + x - 1) / x << " " << maxx << endl;
}

1471B. Strange List

数据拆分，如果 a[i]% x == 0 则可以拆为 a[i] / x 和 a[i] - a[i] / x * x 并加到数组末尾。求数组和。

这道题稍微有点绕，详细看代码。

void solve() {
    int n, x;
    cin >> n >> x;
    ll ans = 0;
    for (int i = 0; i < n; ++i) cin >> a[i], b[i] = a[i], ans += a[i];
    for (int i = 0;; i = (i + 1) % n) {
        if (b[i] % x == 0)
            b[i] /= x, ans += a[i];
        else
            break;
    }
    cout << ans << endl;
}

1471C. Strange Birthday Party

思维性比较强

void solve() {
    int n, m;
    cin >> n >> m;
    ll res = 0, cur = 0;
    ll a[n + 1], b[m + 1];
    for (int i = 1; i <= n; ++i) cin >> a[i];
    for (int j = 1; j <= m; ++j) cin >> b[j];
    sort(a + 1, a + 1 + n);
    for (int i = n; i >= 1; --i) 
        res += b[min(++cur, a[i])];
    cout << res << endl;
}