蓝桥杯历年国赛真题汇总:Here
1.平方末尾
能够表示为某个整数的平方的数字称为“平方数”
比如,25,64
虽然无法立即说出某个数是平方数,但经常可以断定某个数不是平方数。
因为平方数的末位只可能是:[0, 1, 4, 5, 6, 9] 这6个数字中的某个。
所以,4325435332必然不是平方数。
如果给你一个2位或2位以上的数字,你能根据末位的两位来断定它不是平方数吗?
请计算一下,一个2位以上的平方数的最后两位有多少种可能性?
注意:需要提交的是一个整数,表示2位以上的平方数最后两位的不同情况数。
不要填写任何多余内容(比如,说明解释文字等)
答案:22
但由于需要是两位数以上的平方数,所以我们可以直接从4开始
// 枚举即可
set<int>s;
void solve() {
for (int i = 4; i <= 100; ++i) {
s.insert(i * i % 100);
}
cout << s.size();
}
2.反幻方
我国古籍很早就记载着
2 9 4
7 5 3
6 1 8
这是一个三阶幻方。每行每列以及对角线上的数字相加都相等。
下面考虑一个相反的问题。
可不可以用 1~9 的数字填入九宫格。
使得:每行每列每个对角线上的数字和都互不相等呢?
这应该能做到。
比如:
9 1 2
8 4 3
7 5 6
你的任务是搜索所有的三阶反幻方。并统计出一共有多少种。
旋转或镜像算同一种。
比如:
9 1 2
8 4 3
7 5 6
7 8 9
5 4 1
6 3 2
2 1 9
3 4 8
6 5 7
等都算作同一种情况。
请提交三阶反幻方一共多少种。这是一个整数,不要填写任何多余内容。
答案:3120
全排序,得到的最后结果应该是8的倍数(因为一个矩阵的旋转和镜像加上自己本身一共有八个)
int ans = 0;
int b[11], vis[10];
int sum[15];
bool check() {
int n = 0;
for (int i = 0; i < 3; ++i)//行
sum[n++] = b[i * 3 + 1] + b[i * 3 + 2] + b[i * 3 + 3];
for (int i = 1; i < 4; ++i) // 列
sum[n++] = b[i] + b[i + 3] + b[i + 6];
// 对角线
sum[n++] = b[1] + b[5] + b[9];
sum[n++] = b[3] + b[5] + b[7];
sort(sum, sum + n);
for (int i = 1; i < n; ++i)
if (sum[i] == sum[i - 1]) return false;
return true;
}
void dfs(int x) {
if (x == 10) {
ans += check();
return;
}
for (int i = 1; i <= 9; ++i) {
if (!vis[i]) {
vis[i] = 1;
b[x] = i;
dfs(x + 1);
vis[i] = 0;
}
}
}
void solve() {
dfs(1);
cout << ans / 8;
}
3.打印数字
小明写了一个有趣的程序,给定一串数字。
它可以输出这串数字拼出放大的自己的样子。
比如“2016”会输出为:
22222 00000 1 6666
2 2 0 0 1 1 6
2 0 0 1 666666
2 0 0 1 6 6
2 0 0 1 6 6
2 2 0 0 1 6 6
2222222 00000 1111 66666
请仔细分析代码,填写划线部分缺少的内容。
#include <stdio.h>
#include <string.h>
#define ZIW 8
#define ZIH 7
void f(int n) {
char cc[100];
int i, j;
char di[][ZIH][ZIW] = {
{
" 00000 ",
"0 0",
"0 0",
"0 0",
"0 0",
"0 0",
" 00000 "
},
{
" 1 ",
" 1 1 ",
" 1 ",
" 1 ",
" 1 ",
" 1 ",
" 1111"
},
{
" 22222 ",
"2 2",
" 2",
" 2 ",
" 2 ",
" 2 2",
"2222222"
},
{
" 33333 ",
"3 3",
" 3",
" 3333 ",
" 3",
"3 3",
" 33333 "
},
{
" 44 ",
" 4 4 ",
" 4 4 ",
"4 4 ",
"4 4 ",
"4444444",
" 4 "
},
{
" 55555 ",
" 5 ",
"555555 ",
" 5",
" 5",
"5 5",
" 55555 "
},
{
" 6666 ",
"6 ",
"666666 ",
"6 6",
"6 6",
"6 6",
" 66666 "
},
{
"7777777",
"7 7 ",
" 7 ",
" 7 ",
" 7 ",
" 7 ",
" 7 "
},
{
" 88888 ",
"8 8",
"8 8",
" 88888 ",
"8 8",
"8 8",
" 88888 "
},
{
" 99999 ",
"9 9",
"9 9",
" 999999",
" 9",
"9 9",
" 99999 "
}
};
sprintf(cc, "%d", n);
for (i = 0; i < ZIH; i++) { // 7
for (j = 0; j < strlen(cc); j++) { // 2016 ,4
printf("%s ", _______________________ ); //填空位置
}
printf("
");
}
}
int main() {
f(2016);
return 0;
}
注意:只提交划线部分缺少的代码,不要添加任何题面已有代码或符号。
也不要提交任何说明解释文字等。
答案:
di[cc[j] - '0'][i]简单观察即可得出
4.赢球票
某机构举办球票大奖赛。获奖选手有机会赢得若干张球票。
主持人拿出 N 张卡片(上面写着 1~N 的数字),打乱顺序,排成一个圆圈。
你可以从任意一张卡片开始顺时针数数: 1,2,3.....
如果数到的数字刚好和卡片上的数字相同,则把该卡片收入囊中,从下一个卡片重新数数。
直到再无法收获任何卡片,游戏结束。囊中卡片数字的和就是赢得球票的张数。
比如:
卡片排列是:1 2 3
我们从1号卡开始数,就把1号卡拿走。再从2号卡开始,但数的数字无法与卡片对上,
很快数字越来越大,不可能再拿走卡片了。因此这次我们只赢得了1张球票。
还不算太坏!如果我们开始就傻傻地从2或3号卡片数起,那就一张卡片都拿不到了。
如果运气好,卡片排列是 2 1 3
那我们可以顺利拿到所有的卡片!
本题的目标就是:已知顺时针卡片序列。
随便你从哪里开始数,求最多能赢多少张球票(就是收入囊中的卡片数字之和)
输入数据:
第一行一个整数N(N<100),表示卡片数目
第二行 N 个整数,表示顺时针排列的卡片
输出数据:
一行,一个整数,表示最好情况下能赢得多少张球票
比如:
用户输入:
3
1 2 3
程序应该输出:
1
比如:
用户输入:
3
2 1 3
程序应该输出:
6
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
模拟题,由于 n < 100 可以暴力枚举起点
int a[110], n;
int dfs(int x) {
int b[110];
for (int i = 1 ; i <= n; ++i)b[i] = a[i];
int num = 0, idx = 1;
int cnt = 0;
while (idx <= n) {
while (b[x] == -1 and cnt <= n)x++, cnt++;
cnt = 0;
if (b[x] == idx)num += idx, idx = 1, b[x] = -1;
else {
idx++;
}
if (++x == n + 1)x = 1;
}
return num;
}
void solve() {
cin >> n;
for (int i = 1; i <= n; ++i)cin >> a[i];
int cnt = 0;
for (int i = 1; i <= n; ++i) {
cnt = max(cnt, dfs(i));
}
cout << cnt << "
";
}
5.路径之谜
小明冒充X星球的骑士,进入了一个奇怪的城堡。
城堡里边什么都没有,只有方形石头铺成的地面。
假设城堡地面是 n x n 个方格。【如图1.png】所示。
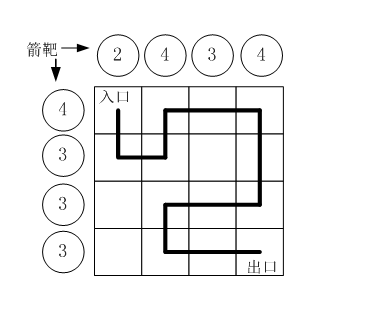
按习俗,骑士要从西北角走到东南角。
可以横向或纵向移动,但不能斜着走,也不能跳跃。
每走到一个新方格,就要向正北方和正西方各射一箭。
(城堡的西墙和北墙内各有 n 个靶子)
同一个方格只允许经过一次。但不必走完所有的方格。
如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?
有时是可以的,比如图1.png中的例子。
本题的要求就是已知箭靶数字,求骑士的行走路径(测试数据保证路径唯一)
输入:
第一行一个整数N(0<N<20),表示地面有 N x N 个方格
第二行N个整数,空格分开,表示北边的箭靶上的数字(自西向东)
第三行N个整数,空格分开,表示西边的箭靶上的数字(自北向南)
输出:
一行若干个整数,表示骑士路径。
为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号: 0,1,2,3....
比如,图1.png中的方块编号为:
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
示例:
用户输入:
4
2 4 3 4
4 3 3 3
程序应该输出:
0 4 5 1 2 3 7 11 10 9 13 14 15
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
思路:
1.第二行N个整数,空格分开,表示北边的箭靶上的数字(自西向东)
第三行N个整数,空格分开,表示西边的箭靶上的数字(自北向南)
这是题目的条件。其实所谓箭靶上的数字就是走到终点的路径,途中所有点访问某行某列的次数
2.知道了箭靶上的数字是什么意思之后,就可以开始dfs了。从左上角的格子开始深搜,当走到了终点,并且行列访问情况与箭靶上的数字符合,就说明找到了答案
int a[25][25], vis[25][25], n, flag; //地图
int r[25], c[25]; //分别代表行和列
vector<int> vec; //用于记录路径
int dir[4][2] = {{ -1, 0}, {1, 0}, {0, -1}, {0, 1}}; //上下左右
int walk_r[25], walk_c[25];
int check() { //检验访问情况是否等于输入
for (int i = 0; i < n; i++) {
if (walk_r[i] != r[i]) return 0;
if (walk_c[i] != c[i]) return 0;
}
return 1;
}
int in(int x, int y) { //判断是否出界
if (x >= 0 && x < n && y >= 0 && y < n) return 1;
return 0;
}
void dfs(int x, int y) {
if (flag == 1) return;
if (x == n - 1 && y == n - 1
&& check()) { //如果走到了终点,并且行列访问情况等于输入
flag = 1; //如果搜到了答案,后面就不需要再搜了
for (int i = 0; i < vec.size(); i++) {
cout << vec[i] << " ";
}
return;
}
for (int i = 0; i < 4; i++) { //上下左右
int tx = x + dir[i][0];
int ty = y + dir[i][1];
if (in(tx, ty)
&& vis[tx][ty] != 1) { //如果没有超界并且没有往回走
vis[tx][ty] = 1;
walk_r[tx]++;
walk_c[ty]++;
vec.push_back(tx * n + ty); //该格子进入路径数组
dfs(tx, ty);
vis[tx][ty] = 0;
walk_r[tx]--;
walk_c[ty]--;
vec.pop_back(); //回溯
}
}
}
void solve() {
cin >> n;
for (int i = 0; i < n; i++) //读入列访问情况
cin >> c[i];
for (int i = 0; i < n; i++) //读入行访问情况
cin >> r[i];
walk_r[0] = 1;
walk_c[0] = 1; //第一个格子访问情况置一
vec.push_back(0);
vis[0][0] = 1;
dfs(0, 0); //当前的坐标是(0,0), 行标记情况,列标记情况
}
6.碱基
生物学家正在对n个物种进行研究。
其中第i个物种的DNA序列为s[i],其中的第j个碱基为s[i][j],碱基一定是A、T、G、C之一。
生物学家想找到这些生物中一部分生物的一些共性,他们现在关注那些至少在m个生物中出现的长度为k的连续碱基序列。准确的说,科学家关心的序列用2m元组( (i1,p1,i2,p2....im,pm) )表示,
满足:
(1<=i1<i2<....<im<=n;)
且对于所有q(0<=q<k), (s[i1][p1+q]=s[i2][p2+q]=....=s[im)][pm+q]。
现在给定所有生物的DNA序列,请告诉科学家有多少的2m元组是需要关注的。如果两个2m元组有任何一个位置不同,则认为是不同的元组。
【输入格式】
输入的第一行包含三个整数n、m、k,两个整数之间用一个空格分隔,意义如题目所述。
接下来n行,每行一个字符串表示一种生物的DNA序列。
DNA序列从1至n编号,每个序列中的碱基从1开始依次编号,不同的生物的DNA序列长度可能不同。
【输出格式】
输出一个整数,表示关注的元组个数。
答案可能很大,你需要输出答案除以 (1000000007) 的余数。
【样例输入】
3 2 2
ATC
TCG
ACG
【样例输出】
2
再例如:
【样例输入】
4 3 3
AAA
AAAA
AAA
AAA
【样例输出】
7
【数据规模与约定】
对于20%的数据,(k<=5),所有字符串总长L满足(L <=100)
对于30%的数据,(L<=10000)
对于60%的数据,(L<=30000)
对于100%的数据,(n<=5,m<=5,1<=k<=L<=100000)
保证所有DNA序列不为空且只会包含’A’ ’G’ ’C’ ’T’四种字母
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
没有理清题意,待补