STL源码学习----lower_bound和upper_bound算法

转自：http://www.cnblogs.com/cobbliu/archive/2012/05/21/2512249.html

先贴一下自己的二分代码：

#include <cstdio>
#include <iostream>
using namespace std;
int a[15]={0,1,5,7,9,13,22,35,63,71,88,89,93};
int main()
{
    //35 7   63 8
    int l=0,r=12,m=(l+r)>>1;
    int p=63;
    while(l<r)
    {
        m=(l+r)>>1;
        //不加等号是upper 加等号是lower
        //upper是找第一个大于的
        //lower是找第一个大于等于的
        if(a[m]>=p) //符合条件 找更符合条件的
        r=m;
        else //不符合条件
        l=m+1;
    }
    printf("%d
",lower_bound(a,a+12,p)-a);
    //最后l=r 取的是l的值就对了
    printf("%d %d %d
",l,r,m);
    return 0;
}

STL中的每个算法都非常精妙，接下来的几天我想集中学习一下STL中的算法。

ForwardIter lower_bound(ForwardIter first, ForwardIter last,const _Tp& val)算法返回一个非递减序列[first, last)中的第一个大于等于值val的位置。

ForwardIter upper_bound(ForwardIter first, ForwardIter last, const _Tp& val)算法返回一个非递减序列[first, last)中第一个大于val的位置。

lower_bound和upper_bound如下图所示：

 

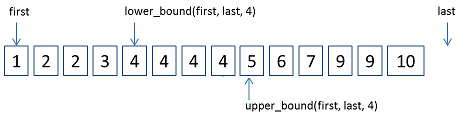
1， lower_bound

　　这个序列中可能会有很多重复的元素，也可能所有的元素都相同，为了充分考虑这种边界条件，STL中的lower_bound算法总体上是才用了二分查找的方法，但是由于是查找序列中的第一个出现的值大于等于val的位置，所以算法要在二分查找的基础上做一些细微的改动。

     首先是我修改数据结构课本上的二分查找实现的lower_bound算法：

int my_lower_bound(int *array, int size, int key)
{
    int first = 0, last = size-1;
    int middle, pos=0;       //需要用pos记录第一个大于等于key的元素位置

    while(first < last)
    {
        middle = (first+last)/2;
        if(array[middle] < key){      //若中位数的值小于key的值，我们要在右边子序列中查找，这时候pos可能是右边子序列的第一个
            first = middle + 1;
            pos = first;
        }
        else{
            last = middle;           //若中位数的值大于等于key，我们要在左边子序列查找，但有可能middle处就是最终位置，所以我们不移动last,
            pos = last;              //而是让first不断逼近last。
        }
    }
    return pos;
}

STL中的实现比较精巧，下面贴出源代码：

//这个算法中，first是最终要返回的位置
int lower_bound(int *array, int size, int key)
{
    int first = 0, middle;
    int half, len;
    len = size;

    while(len > 0) {
        half = len >> 1;
        middle = first + half;
        if(array[middle] < key) {     
            first = middle + 1;          
            len = len-half-1;       //在右边子序列中查找
        }
        else
            len = half;            //在左边子序列（包含middle）中查找
    }
    return first;
}

2， upper_bound

upper_bound返回的是第一个大于val的位置，也是有一个新元素val进来时的插入位置。

我依然将二分查找略做修改：

int my_upper_bound(int *array, int size, int key)
{
    int first = 0, last = size-1;
    int middle, pos = 0;

    while(first < last)
    {
        middle = (first+last)/2;
        if(array[middle] > key){     //当中位数大于key时，last不动，让first不断逼近last
            last = middle;
            pos = last;
        }
        else{
            first = middle + 1;     //当中位数小于等于key时，将first递增，并记录新的位置
            pos = first;
        }
    }
    return pos;
}

下面的代码是STL中的upper_bound实现：

int upper_bound(int *array, int size, int key)
{
    int first = 0, len = size-1;
    int half, middle;

    while(len > 0){
        half = len >> 1;
        middle = first + half;
        if(array[middle] > key)     //中位数大于key,在包含last的左半边序列中查找。
            len = half;
        else{
            first = middle + 1;    //中位数小于等于key,在右半边序列中查找。
            len = len - half - 1;
        }
    }
    return first;
}