BZOJ1146 [CTSC2008]网络管理Network

AC通道：http://www.lydsy.com/JudgeOnline/problem.php?id=1146

题目大意：给你一棵树，每个节点有权值。每次有两种操作：修改某点的权值、询问两个点之间的第k大的权值。

[分析]

　　这题我就不说正解了...貌似是树剖什么的...本人蒟蒻，现在还没学到...

　　

　　讲一讲这题怎么用可持久化线段树做。

　　两点间的第k大，总让人想起区间第k大，然后这题也是带修改的，就让我们想起带修改的区间第k大。

　　这个区间的含义在树上比较含糊了，但是两点间的路径貌似可以用前缀和搞出来?

　　假设前缀的意义是从根节点到这个点的一条链，那么[a,b]可以表示为([root,a]-[root,c))+([root,b]-[root,c])了。

　　

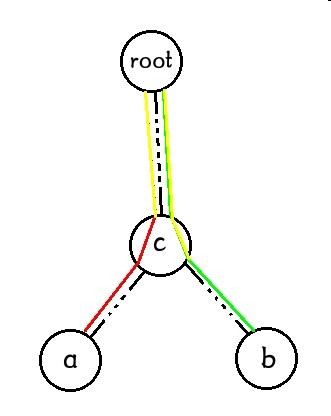
　　那这就和我们的树状数组前缀和靠的比较近了。

　　[注意，我们这里说的前缀，指的是这一条链上所有节点的信息组成的桶，为什么是桶呢?因为区间第k大那题也是桶啊...[其实是因为求第k大的数字，要求第k大显然需要二分数字大小比较咯...]]

　　我们再想想怎么修改。

　　我们每次更新一个点，因为暂且假设我们使用了到根节点这条路为前缀，那么我每次修改就是修改这个节点及它的子树，可想而知，我们不能一个个下去更新，最好能一起更新。

　　也就是说一个点的儿子最好都在连续的一段里[因为联系树状数组的求和，如果在连续的一段里我就只需要在l的位置+1,r+1的位置-1就能同时更新这一段了]

　　满足这个要求的序列...也就是dfs序了。

　　每次更新一个点的时候，设其在dfs序中最先出现的位置为st[i]，最后出现的位置为ed[i](进入记录一次，回溯出来记录一次，如样例：1 2 2 3 5 5 4 4 3 1)

　　那么就在st[i]中将原来的点删去，在ed[i]+1将原来的点加回来。

　　然后在st[i]中将更改后的点加入，在ed[i]+1中将更改后的点删去。

　　[注意：这里说的删除和加入都不是只在这个点加，而是放在整个dfs序组成的树状数组中所带表的删除和加入，即不仅改变这个点i也要改变i+lowbit(i)...等等]

　　这样操作后，每次修改一个值时只会动它所在的子树，不会影响其它的点的前缀[一开始添加也是这样哦]，这样下来每个点在dfs序中的前缀和表示的就是这个点到根这条链上的所有点了。

　　然后查询的时候，利用前缀之间的关系就可以推知这一条链的表示方法，然后就和区间第k大一样了。

　　

　　最后，这题如果你这样打是不够的...因为空间不够。

　　所以我们的dfs序不能那样奢侈的开两个，只能留下第一次遍历到的那一个，这就要求同时记录这个节点的后继节点[即访问完这个节点所在子树后的下一个节点]，每次区间修改就在这两个位置上进行了。

　　

　　献上代码：

　　

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

int in(){
    int x=0;char ch=getchar();
    while(ch>'9' || ch<'0') ch=getchar();
    while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
    return x;
}

const int maxn=80010;

struct Spot{
    int next,data;
}spot[maxn<<1];

#define now spot[pt].data
#define then spot[pt].next

struct Node{
    int l,r,sz;
}s[maxn*120];

int n,m,cnt,key,Sz,ans;
int a[maxn],K[maxn],A[maxn],B[maxn];
int num[maxn<<1],tp,Hash[maxn<<1],hp;
int order[maxn],tail,dic[maxn],nxt[maxn];
int head[maxn],rt[maxn];
int f[maxn][17],depth[maxn];
int Q[4][17];

void add(int u,int v){
    spot[cnt].data=v;spot[cnt].next=head[u];head[u]=cnt++;
    spot[cnt].data=u;spot[cnt].next=head[v];head[v]=cnt++;
}

inline int get_h(int x){
    int l=0,r=hp+1,mid;
    while(l<r-1){
        mid=(l+r)>>1;
        if(Hash[mid]>x) r=mid;
        else l=mid;
    }
    return l;
}

void update(int l,int r,int &rt,int val){
    if(!rt) rt=++Sz; s[rt].sz+=val;
    if(l==r) return;
    int mid=(l+r)>>1;
    if(key<=mid) update(l,mid,s[rt].l,val);
    else update(mid+1,r,s[rt].r,val);
}

inline void renew(int x,int val){
    for(int i=x;i<=n;i+=i&(-i))
        update(1,hp,rt[i],val);
}

void dfs(int last,int x){
    order[++tail]=x;dic[x]=tail;
    for(int i=1;i<17;i++)
        f[x][i]=f[f[x][i-1]][i-1];
    for(int pt=head[x];pt!=-1;pt=then)
        if(now!=last)
            f[now][0]=x,depth[now]=depth[x]+1,dfs(x,now);
    nxt[x]=tail+1;
}

int LCA(int x,int y){
    if(depth[x]<depth[y]) swap(x,y);
    int t=depth[x]-depth[y];
    for(int i=16;i>=0;i--)
        if(t&(1<<i)) x=f[x][i];
    if(x==y) return x;
    for(int i=16;i>=0;i--)
        if(f[x][i]!=f[y][i])
            x=f[x][i],y=f[y][i];
    return f[x][0];
}

int ask(int l,int r,int k){
    if(l==r) return l;
    int sum=0,mid=(l+r)>>1;
    for(int i=0;i<2;i++)
    for(int j=1;j<=Q[i][0];j++) sum+=s[s[Q[i][j]].l].sz;
    for(int i=2;i<4;i++)
    for(int j=1;j<=Q[i][0];j++) sum-=s[s[Q[i][j]].l].sz;
    if(k<=sum){
        for(int i=0;i<4;i++)
        for(int j=1;j<=Q[i][0];j++) Q[i][j]=s[Q[i][j]].l;
        return ask(l,mid,k);
    }
    else{
        for(int i=0;i<4;i++)
        for(int j=1;j<=Q[i][0];j++) Q[i][j]=s[Q[i][j]].r;
        return ask(mid+1,r,k-sum);
    }
}

int query(int k,int l,int r){
    int t=LCA(l,r),All=depth[l]+depth[r]-(depth[t]<<1)+1;
    if(All<k) return -1;
    Q[0][0]=Q[1][0]=Q[2][0]=Q[3][0]=0;
    for(int i=dic[l];i;i-=i&-i) Q[0][++Q[0][0]]=rt[i];
    for(int i=dic[r];i;i-=i&-i) Q[1][++Q[1][0]]=rt[i];
    for(int i=dic[t];i;i-=i&-i) Q[2][++Q[2][0]]=rt[i];
    for(int i=dic[f[t][0]];i;i-=i&-i) Q[3][++Q[3][0]]=rt[i];
    return Hash[ask(1,hp,All-k+1)];
}

void modify(int x,int y){
    key=a[x],renew(dic[x],-1),renew(nxt[x],1);
    key=a[x]=get_h(y),renew(dic[x],1),renew(nxt[x],-1);
}

int main(){
#ifndef ONLINE_JUDGE
    freopen("114610.in","r",stdin);
    freopen("1146.out","w",stdout);
#endif
    
    int u,v,p;
    
    n=in();m=in();
    for(int i=1;i<=n;i++)
        a[i]=in(),num[++tp]=a[i],head[i]=-1;
    for(int i=1;i<n;i++)
        u=in(),v=in(),add(u,v);
    for(int i=1;i<=m;i++){
        K[i]=in(),A[i]=in(),B[i]=in();
        if(!K[i]) num[++tp]=B[i];
    }
    sort(num+1,num+tp+1);
    Hash[++hp]=num[1];
    for(int i=2;i<=tp;i++)
        if(num[i]!=num[i-1]) Hash[++hp]=num[i];
    
    dfs(0,1);
    for(int i=1;i<=n;i++) a[i]=get_h(a[i]);
    for(int i=1;i<=n;i++)
        key=a[i],renew(dic[i],1),renew(nxt[i],-1);
    
    for(int i=1;i<=m;i++)
        if(K[i]){
            ans=query(K[i],A[i],B[i]);
            if(ans>0) printf("%d
",ans);
            else puts("invalid request!");
        }
        else modify(A[i],B[i]);

    return 0;
}