A
题意:
给定一个时间点t与n种车,每种车首班车时间给定,间隔时间不变,问从t点开始能最先坐上哪一辆车。
题解:
基础的模拟,不多赘述。
1 #include<iostream>
2 #include<algorithm>
3 #include<cmath>
4 #include<vector>
5 #include<string>
6 #include<queue>
7 #include<stack>
8 using namespace std;
9 int n,t,s,d,ans=2147483640,ansp;
10 int main(){
11 ios::sync_with_stdio(false);
12 cin>>n>>t;
13 for (int i=1; i<=n; i++) {
14 cin>>s>>d;
15 int now=s;
16 while (now<t) now+=d;
17 if (now-t<ans) ans=now-t,ansp=i;
18 //ans=min(now-t,ans);
19 }
20 cout<<ansp<<endl;
21 return 0;
22 }
B
题意:
有一堆积木,可以用一个二维平面,每个单元有一个高度数值来表示。现给出从积木前方、左方、上方看的形状,需构造一种方案,满足所有情况。
题解:
因为有多种情况,只需给出一种即可,所以就先考虑从上往下看的情况。当从上往下看有积木时,此单元的高度设成此点横竖两条看去的高度的较小值即可。
1 #include<iostream>
2 #include<algorithm>
3 #include<cmath>
4 #include<vector>
5 #include<string>
6 #include<queue>
7 #include<stack>
8 using namespace std;
9 int n,m,h;
10 int a[107],b[107],c[107][107],ans[107][107];
11 int main(){
12 ios::sync_with_stdio(false);
13 cin>>n>>m>>h;
14 for (int i=1; i<=m; i++) cin>>a[i];
15 for (int i=1; i<=n; i++) cin>>b[i];
16 for (int i=1; i<=n; i++)
17 for (int j=1; j<=m; j++)
18 cin>>c[i][j];
19 for (int i=1; i<=n; i++)
20 for (int j=1; j<=m; j++) if (c[i][j]==1){
21 ans[i][j]=min(b[i],a[j]);
22 }
23 for (int i=1; i<=n; i++) {
24 for (int j=1; j<=m; j++) cout<<ans[i][j]<<" ";
25 cout<<endl;
26 }
27 return 0;
28 }
C
题意:
给定一个字符串,只由 ?( ) 组成,
?可以是 ( 也可以是 ) 现定义一个字符串是正确的,当且仅当每一个左括号能在它后方找到一个右括号与之相匹配。
现构造一个字符串,使得整个字符串是正确的,但是它的每一个前缀都是不正确的(不包括空字符串和它自己)
题解:
主要还是细节方面,首先是无解情况的特判。
当第一个字符为)或最后一个字符为(时都是无解;当字符串长度为奇数时,也是无解。
然后是字符串中?的策略。
当(的数量在字符串长度一半以下(要把后面没有遍历到的括号也先预处理一起算上)时,就先把?定为(。
否则再定为)。
在遍历过程中也许进行无解情况的特判,从左到当前位置记录(和)的数量,当左括号数量小于右括号数量时,即无解(整个字符串无法正确)
而当在遍历过程中某一时刻,左括号等于右括号数量时,也是无解(字符串的子集是正确的,不符合条件)
这道题细节也比较多,每个人都有自己不同的方法,主要还是想出一个关于?的解决方案。
1 #include<iostream>
2 #include<algorithm>
3 #include<cmath>
4 #include<vector>
5 #include<string>
6 #include<queue>
7 #include<stack>
8 using namespace std;
9 int len,cntl,cntr,firl,firr,fira;
10 string s,ans;
11 int main(){
12 ios::sync_with_stdio(false);
13 cin>>len;
14 cin>>s;
15 if (s[0]==')' || s[len-1]=='('){cout<<":("<<endl; return 0;}
16 if (len%2!=0){cout<<":("<<endl; return 0;}
17 for (int i=0; i<len; i++) {
18 if (s[i]=='(') firl++;
19 else if (s[i]==')') firr++;
20 else fira++;
21 }
22 if (firl>(len/2) || firr>(len/2)) {cout<<":("<<endl; return 0;}
23 for (int i=0; i<len; i++) {
24 if (s[i]=='(') cntl++,ans+='(';
25 if (s[i]==')') cntr++,ans+=')';
26 //if (cntl>(len/2) || cntr>(len/2)) {cout<<":("<<endl; return 0;}
27 //if (cntr>cntl) {cout<<":("<<endl; return 0;}
28 if (s[i]=='?' && i!=len-1) {
29 if (firl<(len/2)) {cntl++,ans+='('; firl++;}
30 else
31 if (cntl-cntr>1 && firr<(len/2)) {cntr++;ans+=')';firr++;}
32 }
33 if (s[i]=='?' && i==len-1) {
34 cntr++,ans+=')';
35 }
36 if (cntl<cntr) {cout<<":("<<endl; return 0;}
37 if (i<len-1 && cntl==cntr) {cout<<":("<<endl; return 0;}
38 }
39 if (cntl!=cntr) {cout<<":("<<endl; return 0;}
40 cout<<ans<<endl;
41 return 0;
42 }
D
题意:
有一棵已节点1为根的数,每个节点有一个max或者min属性,代表这个点等于它所有儿子(仅一代)的max或min值。现假设有k个叶子节点,可把它们赋值1~k。求一种复制方案使得根的值最大。
题解:
这道题的官方题解不是很容易理解,这里尽可能地有一种易懂的方式来讲述。
因为根的值肯定是从所有的叶子结点当中来选出一个,所以需要考虑一种从叶子节点传到根的方法。
于是会想到dp,因为题目要求根数值尽量大,所以定义f[i]表示i这个节点能取到的最大的值是它下属叶子结点中的第f[i]大。
首先,当这个节点属性是min时,很容易想到f[i]=∑f[j](j为i的儿子)
而当属性是max时,f[i]=min(f[j]) (j为i的儿子)
很重要的一点是,根的值只需要从1个叶子节点中取到,而所有的叶子结点的值是可以自己安排的,所以说才可以直接取min。
等传到根以后把最大的值安排在每一层所取的那个节点下属的叶子结点即可。
时间复杂度为O(n)。
1 #include<iostream> 2 #include<algorithm> 3 #include<vector> 4 using namespace std; 5 const int maxn=300007; 6 int n,op[maxn],k,f[maxn]; 7 vector <int> a[maxn]; 8 void dfs(int u,int p) { 9 for (int i=0; i<a[u].size(); i++) { 10 int v=a[u][i]; 11 if (v==p) continue; 12 dfs(v,u); 13 if (op[u]==0) f[u]+=f[v]; 14 else { 15 if (!f[u]) f[u]=f[v]; 16 else f[u]=min(f[u],f[v]); 17 } 18 } 19 20 } 21 int main(){ 22 ios::sync_with_stdio(false); 23 cin>>n; 24 for (int i=1; i<=n; i++) cin>>op[i]; 25 for (int i=2; i<=n; i++) { 26 int p; 27 cin>>p; 28 a[p].push_back(i); 29 a[i].push_back(p); 30 } 31 for (int i=2; i<=n; i++) if (a[i].size()==1) f[i]=1,k++; 32 dfs(1,0); 33 cout<<k+1-f[1]<<endl; 34 return 0; 35 }
E
题意:
交互题,有一个n×n的方格,里面有一条蛇。蛇的身体由一个个小方块拼接而成。
现在有2018次询问,可以询问一个二维空间内线段经过它边界的次数。最后求蛇头与蛇尾。
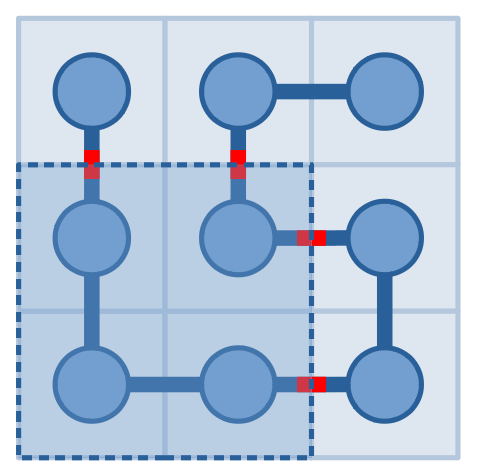
题解:
首先需要发现一个规律,当查询区间内有且只有蛇头或蛇尾中的一个时,查询出来的答案是奇数,其余时候是偶数。
规定最多可以用2019次询问,n的范围是1000。从数据范围中也可以猜测,是横竖各扫一遍,然后再进行一些细节操作。
先横着扫一遍,如果扫到有两列答案是奇数的,分别在列里进行二分即可求出答案。
当横着扫全部是偶数的情况下,代表这两个点在一列里。由于点不能重复,所以这两点肯定不在同一行里。
竖着扫一遍,找到第一个奇数行的时候进行二分。注意,在找到第二个奇数行时不用再进行二分了,因为它的列已经知道了。
这样查询次数最多就是2019次。
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 struct data 5 { 6 int x,y; 7 }ans[10]; 8 int n,cnt=0; 9 int query(int x1, int y1, int x2, int y2) 10 { 11 int res; 12 printf("? %d %d %d %d ", x1, y1, x2, y2); 13 fflush(stdout); 14 scanf("%d",&res); 15 return res; 16 } 17 data solve1(int p) 18 { 19 data res; 20 int l = 0,r = n; 21 while (l + 1 < r) 22 { 23 int mid = (l + r) >> 1; 24 if (query(p, l+1, p, mid) & 1!=0) r = mid; 25 else l = mid; 26 } 27 res.x = p; 28 res.y = r; 29 return res; 30 } 31 data solve2(int p) 32 { 33 data res; 34 int l = 0,r = n; 35 while (l + 1 < r) 36 { 37 int mid = (l + r) >> 1; 38 if (query(l+1, p, mid, p) & 1!=0) r = mid; 39 else l = mid; 40 } 41 res.x = r; 42 res.y = p; 43 return res; 44 } 45 int main() 46 { 47 ios::sync_with_stdio(false); 48 cin>>n; 49 for (int i=1; i<=n; i++) 50 { 51 int now = query(i, 1, i, n); 52 if (now & 1!=0) ans[++cnt] = solve1(i); 53 } 54 if (cnt==0) 55 { 56 for (int i=1; i<=n; i++) 57 { 58 int now = query(1, i, n, i); 59 if (now & 1!=0) 60 { 61 if (cnt==0) ans[++cnt] = solve2(i); 62 else 63 { 64 data a2; 65 a2.x = ans[1].x; 66 a2.y = i; 67 ans[++cnt] = a2; 68 } 69 } 70 } 71 } 72 printf("! %d %d %d %d ",ans[1].x, ans[1].y, ans[2].x, ans[2].y); 73 fflush(stdout); 74 return 0; 75 }