Time Limit: 3000 ms Memory Limit: 256 MB
Description
给你一个无限长的数组,初始的时候都为0,有3种操作:
操作1是把给定区间$[l,r]$设为1,
操作2是把给定区间$[l,r]$设为0,
操作3把给定区间$[l,r]$0,1反转。
一共n个操作,每次操作后要输出最小位置的0。
Input
第一行一个整数n,表示有n个操作
接下来n行,每行3个整数op,l,r表示一个操作
Output
共n行,一行一个整数表示答案
Sample Input |
Sample Output |
3
1 3 4
3 1 6
2 1 3
|
1
3
1
|
HINT
对于30%的数据$1le nle 10^3,1le lle rle 10^{18}$
对于100%的数据$1le nle 10^5,1le lle rle 10^{18}$
题解
离散化操作区间:
首先看到$1le lle rle 10^{18}$的范围,第一反应离散化。
这题的离散化是非常讲究的,我们不能只把每个区间操作的两端点提取出来离散化(我就是这么干的,其他部分都是对的,结果眼睁睁地没法输出),因为这样无法考虑到区间之间的点,如下图:
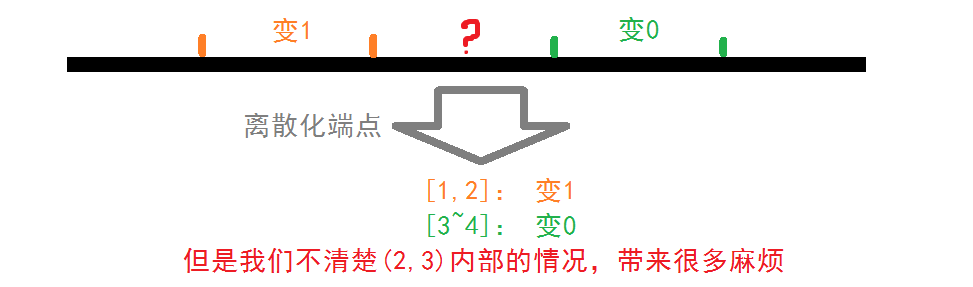
考虑到答案的位置,答案应该只可能出现在某一段操作区间右端点的右边一位,于是我们在离散一个操作区间$l,r$的同时,把$r+1$也离散化掉。操作并不涉及到$r+1$,仅仅是为了输出答案的正确和可行性。
实现修改操作:
看到熟悉的区间操作,当然要想想线段树啦。
这里采用两棵线段树的写法实现3种操作,当然也有一棵线段树搞定的写法。
两棵线段树$A,B$,都先按照离散化的规模建好,以离散化端点编号为索引。$A$记录$0$的信息,$B$记录$1$的信息。
线段树维护的信息是:$0$或$1$最左出现的位置。
第1个操作:将$A$的相应区间的信息清空(设置成最大值,因为不存在$0$了),将$B$的相应区间的信息填充(设置成区间的左端点位置),并打上清空或填充标记。日后记得下传。
第2个操作:与第1个操作完全相反。
第3个操作:将$A$的相应区间节点和$B$的相应区间节点对调。
输出:
询问$A$中的最小值位置,输出离散化前的原值即可。可以发现这个点一定是某个区间的$r$再$+1$。
时间复杂度$O(n lg n)$,空间复杂度$O(n)$。

1 #include <cstdio> 2 #include <algorithm> 3 #define min(a,b) (a<b?a:b) 4 using namespace std; 5 typedef long long ll; 6 const int N=1e5+10; 7 ll INF=1000000000000000001; 8 int n,lshtot,opt[N][3],total; 9 ll inp[N][3],lis[N*3],minloc,maxloc,orival[N*3]; 10 void lshAndfill(){ 11 sort(lis+1,lis+1+lshtot); 12 total=unique(lis+1,lis+1+lshtot)-lis-1; 13 for(int i=1;i<=total;i++) orival[i]=lis[i]; 14 orival[total+1]=INF; 15 for(int i=1;i<=n;i++){ 16 opt[i][0]=inp[i][0]; 17 opt[i][1]=lower_bound(lis+1,lis+1+total,inp[i][1])-lis; 18 opt[i][2]=lower_bound(lis+1,lis+1+total,inp[i][2])-lis; 19 } 20 } 21 struct Seg{ 22 int cnt,root[2],sz,ch[N*13][2],mark[N*13]; 23 ll info[N*13]; 24 void build(int Size){ 25 sz=Size; 26 _build(root[0],1,sz,true); 27 _build(root[1],1,sz,false); 28 } 29 void _build(int &u,int l,int r,bool isfill){ 30 if(!u) u=++cnt; 31 mark[u]=-1; 32 if(l==r){ 33 if(isfill) info[u]=l; 34 else info[u]=total+1; 35 return; 36 } 37 int mid=(l+r)>>1; 38 _build(ch[u][0],l,mid,isfill); 39 _build(ch[u][1],mid+1,r,isfill); 40 pushup(u); 41 } 42 inline void pushup(int u){ 43 info[u]=min(info[ch[u][0]],info[ch[u][1]]); 44 } 45 inline void pushdown(int u,int l,int r){ 46 int lc=ch[u][0],rc=ch[u][1]; 47 if(mark[u]==-1) return; 48 mark[lc]=mark[rc]=mark[u]; 49 if(mark[u]==0) 50 info[lc]=info[rc]=total+1; 51 else{ 52 info[lc]=l; 53 info[rc]=(l+r)/2+1; 54 } 55 mark[u]=-1; 56 } 57 void setSeg(int flag,int l,int r){ 58 _setSeg(root[0^flag],root[1^flag],1,sz,l,r); 59 } 60 void _setSeg(int u1,int u2,int l,int r,int L,int R){ 61 if(L<=l&&r<=R){ 62 info[u1]=total+1; 63 info[u2]=l; 64 mark[u1]=0; mark[u2]=1; 65 return; 66 } 67 pushdown(u1,l,r); 68 pushdown(u2,l,r); 69 int mid=(l+r)>>1; 70 if(L<=mid) _setSeg(ch[u1][0],ch[u2][0],l,mid,L,R); 71 if(mid<R) _setSeg(ch[u1][1],ch[u2][1],mid+1,r,L,R); 72 pushup(u1); 73 pushup(u2); 74 } 75 void swapSeg(int l,int r){_swapSeg(root[0],root[1],1,sz,l,r);} 76 void _swapSeg(int &u1,int &u2,int l,int r,int L,int R){ 77 if(L<=l&&r<=R){ 78 swap(u1,u2); 79 return; 80 } 81 pushdown(u1,l,r); 82 pushdown(u2,l,r); 83 int mid=(l+r)>>1; 84 if(L<=mid) _swapSeg(ch[u1][0],ch[u2][0],l,mid,L,R); 85 if(mid<R) _swapSeg(ch[u1][1],ch[u2][1],mid+1,r,L,R); 86 pushup(u1); 87 pushup(u2); 88 } 89 inline ll getMin(int x){return info[root[x]];} 90 }seg; 91 int main(){ 92 scanf("%d",&n); 93 minloc=-1; 94 for(int i=1;i<=n;i++){ 95 scanf("%lld%lld%lld",&inp[i][0],&inp[i][1],&inp[i][2]); 96 lis[++lshtot]=inp[i][1]; 97 lis[++lshtot]=inp[i][2]; 98 lis[++lshtot]=inp[i][2]+1; 99 if(minloc==-1) minloc=min(inp[i][1],inp[i][2]); 100 else minloc=min(minloc,min(inp[i][1],inp[i][2])); 101 } 102 lshAndfill(); 103 seg.build(total); 104 for(int i=1;i<=n;i++){ 105 if(minloc>1){ 106 printf("1 "); 107 continue; 108 } 109 if(opt[i][0]<=2) 110 seg.setSeg(opt[i][0]==2,opt[i][1],opt[i][2]); 111 else 112 seg.swapSeg(opt[i][1],opt[i][2]); 113 printf("%lld ",orival[seg.getMin(0)]); 114 } 115 return 0; 116 }
