简介
动态树分治整体上由点分治发展而来。
点分治是统计树上路径,而动态树分治用来统计与点有关的树上路径,比如多次询问某一些点到询问点的距离和。
前置知识就是点分治。
做法
众所周知,点分树(点分治中重心组成的树)的深度是$O(lgn)$的。
要统计树上的路径,等价为统计经过每个点的路径。那么就统计经过每个重心的路径。
拿一道题目来讲比较具体:BZOJ4012。有一棵带点权边权的树,多次询问$(u,l,r)$,表示询问点权在$[l,r]$内的点到$u$的距离和。
比如一个重心$u$,其管辖范围为$S_u$,询问的点$q$在$v$子树内:
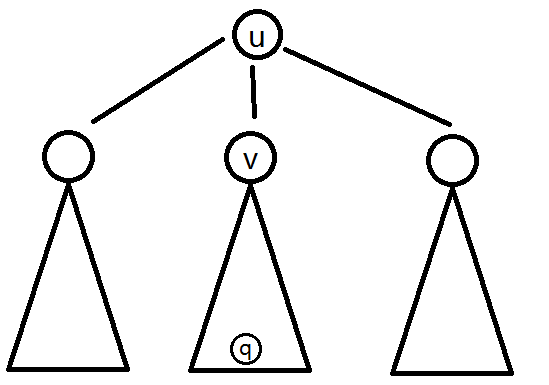
那么应该用其它两棵子树内所有符合的点到$u$的距离和 + $q$到$u$的距离乘上其它子树内符合的点的个数,就是经过这个重心的答案。
注意到我们需要容斥:用$u$的信息斥去$v$的信息才能得到划线部分的值,这和点分治的做法大致相同。
方便点来说,$v$子树的重心$v'$,除了要像$u$一样记录$S_v'$内所有点到它的信息,还要记录$S_v'$内所有点到$u$的信息,也就是到点分父亲的信息。原理上是和点分治一模一样的容斥,只不过为了方便,应该把这个信息放在子树的重心记录。
完整做法如下:
对于点分树上的每一个重心$u$:记其管辖范围为$S_u$。
求出$S_u$内每一个点到$u$的距离值。
对$S_u$内每一个点按照点权由小至大排序,求出排序后距离值的前缀和。
对$u$的每一个后继$v$,若$v$子树的重心为$v'$,求出$S_v'$内所有点到$u$的距离值,对它们按照点权由小至大排序,求出排序后距离值的前缀和。
calc1(u,l,r)表示求$S_u$内权值为$[l,r]$的点到$u$的距离和,由于已经按照权值排序,又有前缀和,可以二分得出$l$和$r$的位置,返回前缀和。
calc2(u,l,r)表示求$S_u$内权值为$[l,r]$的点到$u$的点分父亲的距离和,求法同上。
size(u,l,r)表示求$S_u$内权值为$[l,r]$的点有多少个,求法同上二分。
dis(x,y)表示求原树上$x$~$y$的距离。
查询$(u,l,r)$
对于$u$和$u$的所有点分树祖先,记为$x$,设$u$在$x$的$y$子树中:
$ans+=dis(u,x)*[size(x,l,r)-size(y,l,r)]+calc1(x,l,r)-calc2(y,l,r)$
1 #include <cstdio> 2 #include <algorithm> 3 #include <vector> 4 #define mp make_pair 5 using namespace std; 6 typedef long long ll; 7 typedef pair<int,int> pii; 8 const int N=150010,INF=2147000000,Bas=20; 9 int n,q,A,a[N],h[N],tot; //权值和边 10 int pre[N][Bas],dep[N],dist[N]; //倍增lca 点到根节点的深度和距离 11 int cut[N],fa[N];//点分区块断点,点分树父亲 12 int size[N],mins,minu; //找重心 13 struct Edge{int v,next,w;}g[N*2]; //树边 14 vector<pii> lis[N],lisf[N]; //每个重心的数据列表 每个重心相对于点分父亲的数据列表 15 vector<ll> sum[N],sumf[N]; //每个重心列表按权值排序后距离前缀和 每个重心相对于点分父亲的列表按权值排序后距离前缀和 16 inline int rd(){ 17 int x=0; 18 char c; 19 while((c=getchar())<'0'||c>'9'); 20 x=c-'0'; 21 while('0'<=(c=getchar())&&c<='9') x=x*10+c-'0'; 22 return x; 23 } 24 inline int min(int x,int y){return x<y?x:y;} 25 inline int max(int x,int y){return x>y?x:y;} 26 inline void swap(int &x,int &y){int t=x;x=y;y=t;} 27 inline void addEdge(int u,int v,int w){ 28 g[++tot].v=v; g[tot].w=w; g[tot].next=h[u]; h[u]=tot; 29 g[++tot].v=u; g[tot].w=w; g[tot].next=h[v]; h[v]=tot; 30 } 31 void predfs(int u,int fa,int Dep,int Dist){//计算11行的数组 32 dep[u]=Dep; 33 dist[u]=Dist; 34 pre[u][0]=fa; 35 for(int i=1;i<Bas;i++) pre[u][i]=pre[pre[u][i-1]][i-1]; 36 for(int i=h[u],v;i;i=g[i].next) 37 if((v=g[i].v)!=fa) 38 predfs(v,u,Dep+1,Dist+g[i].w); 39 } 40 int getlca(int a,int b){ 41 if(dep[a]<dep[b]) swap(a,b); 42 for(int i=Bas-1;i>=0;i--) 43 if(dep[pre[a][i]]>=dep[b]) a=pre[a][i]; 44 if(a==b) return a; 45 for(int i=Bas-1;i>=0;i--) 46 if(pre[a][i]!=pre[b][i]) a=pre[a][i],b=pre[b][i]; 47 return pre[a][0]; 48 } 49 int getdis(int x,int y){ 50 int lca=getlca(x,y); 51 return dist[x]-dist[lca]+dist[y]-dist[lca]; 52 } 53 void dfs1(int u,int fa){//找重心 54 size[u]=1; 55 for(int i=h[u],v;i;i=g[i].next) 56 if(!cut[v=g[i].v]&&v!=fa){ 57 dfs1(v,u); 58 size[u]+=size[v]; 59 } 60 } 61 void dfs2(int u,int fa,int all){//找重心 62 int maxt=0; 63 for(int i=h[u],v;i;i=g[i].next) 64 if(!cut[v=g[i].v]&&v!=fa){ 65 dfs2(v,u,all); 66 if(size[v]>maxt) maxt=size[v]; 67 } 68 if(all-size[u]>maxt) maxt=all-size[u]; 69 if(maxt<mins) mins=maxt,minu=u; 70 } 71 int getroot(int u){//找重心 72 mins=INF; minu=0; 73 dfs1(u,0); 74 dfs2(u,0,size[u]); 75 return minu; 76 } 77 void collect(int u,int fa,int dis,int st,int type){//收集数据至重心st的列表 78 if(!type) lis[st].push_back(mp(a[u],dis)); 79 else lisf[st].push_back(mp(a[u],dis)); 80 for(int i=h[u],v;i;i=g[i].next) 81 if(!cut[v=g[i].v]&&v!=fa) 82 collect(v,u,dis+g[i].w,st,type); 83 } 84 int find(vector<pii> &u,int x,int type){//以权值为关键字,lowerbound或upperbound x的位置 85 int l=0,r=u.size()-1,mid; 86 while(l<=r){ 87 mid=(l+r)>>1; 88 if((!type&&x<=u[mid].first)||(type&&x<u[mid].first)) r=mid-1; 89 else l=mid+1; 90 } 91 return l; 92 } 93 ll calc(vector<pii> &u,vector<ll> &s,int l,int r,int type){//计算列表在l~r的点的距离和或个数 94 int pos1=find(u,l,0); 95 int pos2=find(u,r,1)-1; 96 if(pos2<pos1) return 0; 97 if(pos1==0){ 98 if(!type) return s[min(u.size()-1,pos2)]; 99 else return min(u.size()-1,pos2)+1; 100 } 101 if(!type) 102 return s[min(u.size()-1,pos2)]-s[max(0,pos1-1)]; 103 else 104 return min(u.size()-1,pos2)-max(0,pos1)+1; 105 } 106 int solve(int rt,int faedge){//预处理 107 int u=getroot(rt); 108 collect(u,0,0,u,0); 109 sort(lis[u].begin(),lis[u].end()); 110 ll x=0; 111 for(int i=0,sz=lis[u].size();i<sz;i++){ 112 x+=lis[u][i].second; 113 sum[u].push_back(x); 114 } 115 if(faedge){ 116 collect(rt,0,faedge,u,1); 117 sort(lisf[u].begin(),lisf[u].end()); 118 x=0; 119 for(int i=0,sz=lisf[u].size();i<sz;i++){ 120 x+=lisf[u][i].second; 121 sumf[u].push_back(x); 122 } 123 } 124 cut[u]=1; 125 for(int i=h[u],v;i;i=g[i].next) 126 if(!cut[v=g[i].v]) 127 fa[solve(v,g[i].w)]=u; 128 return u; 129 } 130 ll query(int st,int u,int l,int r,ll sonsum,int sonsize){//询问 131 ll ret=0; 132 if(fa[u]) ret=query(st,fa[u],l,r,calc(lisf[u],sumf[u],l,r,0),calc(lisf[u],sumf[u],l,r,1)); 133 ret+=1LL*getdis(st,u)*(calc(lis[u],sum[u],l,r,1)-sonsize)+calc(lis[u],sum[u],l,r,0)-sonsum; 134 return ret; 135 } 136 int main(){ 137 n=rd(); q=rd(); A=rd(); 138 for(int i=1;i<=n;i++) a[i]=rd(); 139 for(int i=1,u,v,w;i<n;i++){ 140 u=rd();v=rd();w=rd(); 141 addEdge(u,v,w); 142 } 143 predfs(1,0,1,0); 144 solve(1,0); 145 int u,l,r; 146 ll ans=0; 147 while(q--){ 148 u=rd(); l=rd(); r=rd(); 149 l=(l+ans)%A; r=(r+ans)%A; 150 if(l>r) swap(l,r); 151 ans=query(u,u,l,r,0,0); 152 printf("%lld ",ans); 153 } 154 return 0; 155 }