Description


Sample Input
15 5
1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 1 2 2 3 3 4 4 5 5 6 6 7 7
1 2
8 11
5 8
8 15
4 6
Sample Output
1
5
4
7
3
HINT
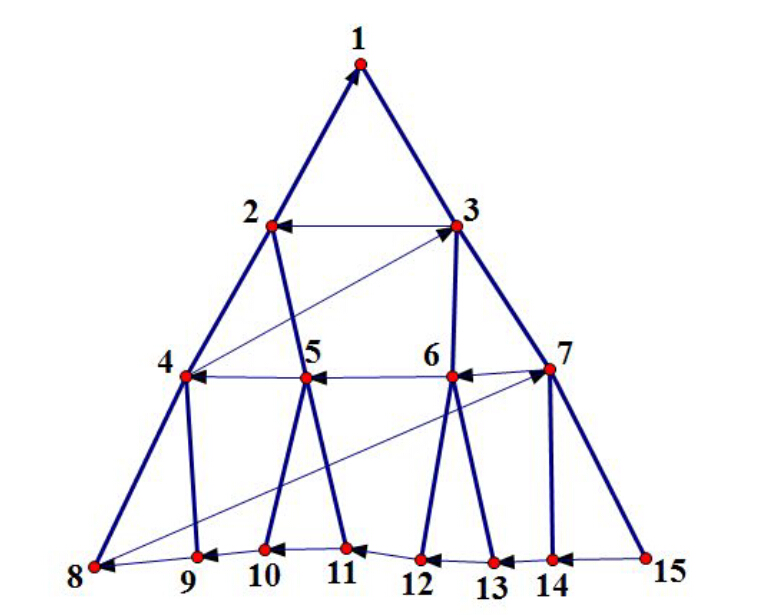
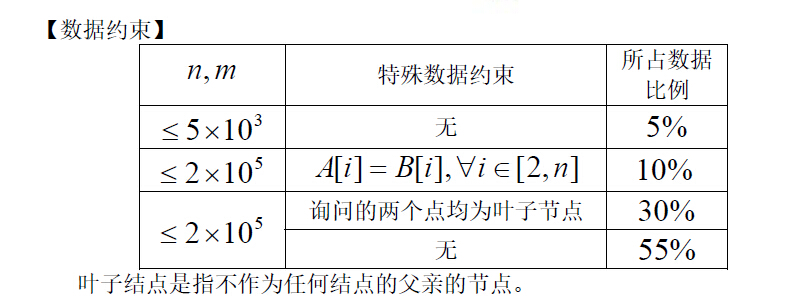
Solution
题目求的”最近公共祖先“,实际上是所有公共祖先中编号最大的那一个......
看看怎么把两棵树联系起来。
要同时维护询问的两个点的祖先的并集比较困难,考虑能不能离线简化一下问题。
我们dfs遍历A树,每走到A树的一个点u,回答所有形如(u,v)的询问,其中v是B树上的点。
注意到遍历到u时,根节点到u的路径构成了u的祖先集合F_u。于是我们就可以转化一下问题,对于每个询问,相当于询问在F_u中,是v在B树中的祖先的最大值。
预处理出A树中每一个点在B树中的dfn出序和入序,以此刻画出A树的每一个点在B树中对应哪一棵子树。在A树中每遍历到一个点,就给B树中的相应子树中的所有点更新最大值。这些操作用线段树维护B树的dfn序实现。此时问题变得非常简单,此时只需要回答v在线段树中相应位置的值即可。
注意到A树的dfs有回溯操作,所以用主席树解决就可以了。主席树是区间修改、单点查询,注意标记永久化。
这题的关键就在于如何转化询问,使得问题变得易于维护。
#include <cstdio>
#include <vector>
#define pb push_back
#define mp make_pair
using namespace std;
typedef pair<int,int> pii;
const int N=200005;
int n,m,out[N];
int ha[N],hb[N],tot;
int dfnb[N][2],dfntm;
vector<pii> q[N];
struct Edge{int v,next;}e[N*2];
inline void addEdge(int u,int v,int *h){e[++tot]=(Edge){v,h[u]};h[u]=tot;}
namespace CEG{/*{{{*/
const int S=N*2*18;
int rt[N],sz,ch[S][2],maxs[S];
inline int copy(int u){
int v=++sz;
ch[v][0]=ch[u][0]; ch[v][1]=ch[u][1];
maxs[v]=maxs[u];
return v;
}
void insert(int u,int &v,int l,int r,int L,int R,int x){
v=copy(u);
if(L<=l&&r<=R){
maxs[v]=max(maxs[v],x);
return;
}
int mid=(l+r)>>1;
if(R<=mid) insert(ch[u][0],ch[v][0],l,mid,L,R,x);
else if(mid<L) insert(ch[u][1],ch[v][1],mid+1,r,L,R,x);
else{
insert(ch[u][0],ch[v][0],l,mid,L,mid,x);
insert(ch[u][1],ch[v][1],mid+1,r,mid+1,R,x);
}
}
int query(int u,int l,int r,int pos,int now){
now=max(now,maxs[u]);
if(l==r) return now;
int mid=(l+r)>>1;
if(pos<=mid) return query(ch[u][0],l,mid,pos,now);
else return query(ch[u][1],mid+1,r,pos,now);
}
}/*}}}*/
void dfsB(int u,int fa){
dfnb[u][0]=++dfntm;
for(int i=hb[u],v;i;i=e[i].next)
if((v=e[i].v)!=fa)
dfsB(v,u);
dfnb[u][1]=dfntm;
}
void dfsA(int u,int fa){
CEG::insert(CEG::rt[fa],CEG::rt[u],1,n,dfnb[u][0],dfnb[u][1],u);
for(int i=0,sz=q[u].size();i<sz;i++){
int v=q[u][i].first,qid=q[u][i].second;
out[qid]=CEG::query(CEG::rt[u],1,n,dfnb[v][0],0);
}
for(int i=ha[u],v;i;i=e[i].next)
if((v=e[i].v)!=fa)
dfsA(v,u);
}
int main(){
freopen("input.in","r",stdin);
scanf("%d%d",&n,&m);
for(int v=2;v<=n;v++){
int u;
scanf("%d",&u);
addEdge(u,v,ha);
}
for(int v=2;v<=n;v++){
int u;
scanf("%d",&u);
addEdge(u,v,hb);
}
for(int i=1;i<=m;i++){
int x,y;
scanf("%d%d",&x,&y);
q[x].pb(mp(y,i));
}
dfsB(1,0);
dfsA(1,0);
for(int i=1;i<=m;i++) printf("%d
",out[i]);
return 0;
}