快速幂定义: 1.快速幂就是快速算底数的n次幂。其时间复杂度为 O(log₂N), 与朴素的O(N)相比效率有了极大的提高。用法:用于求解 a 的 b 次方,而b是一个非常大的数,用O(n)的复杂度会超时。那么就需要这个算法,注意它不但可以对数求次幂,而且可用于矩阵快速幂。--百度百科
2.所谓的快速幂,实际上是快速幂取模的缩写,简单的说,就是快速的求一个幂式的模(余)。在程序设计过程中,经常要去求一些大数对于某个数的余数,为了得到更快、计算范围更大的算法,产生了快速幂取模算法 --http://blog.csdn.net/xuruoxin/article/details/8578992

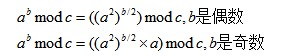
模运算规则:
模运算与基本四则运算有些相似,但是除法例外。其规则如下:
(a + b) % p = (a % p + b % p) % p
(a – b) % p = (a % p – b % p) % p
(a * b) % p = (a % p * b % p) % p
ab % p = ((a % p)b) % p
结合率:
((a+b) % p + c) % p = (a + (b+c) % p) % p
((a*b) % p * c)% p = (a * (b*c) % p) % p
可能你会问了这个算法有什么用呢?其实用的更多是使用矩阵快速幂,算递推式,注意是递推式,简单的如斐波那契数列的第一亿项的结果模上10000000后是多少你还能用递推式去,逐项递推吗?当然不能,这里就可以发挥矩阵快速幂的神威了,那斐波那契数列和矩阵快速幂能有一毛钱的关系?答案是有而且很大。
a的b次方可以用pow(a, b)是数学头文件math.h里面有的函数
但是返回值是double类型 + 数据有精度误差···那么自己写for循环吧
1 LL pow(LL a, LL b){ //a的b次方 2 LL ret = 1; 3 for(LL i = 1; i <= b; i ++){ 4 ret *= a; 5 } 6 return ret; 7 }
若题目b的范围是1 <= b <= 1e9···那么会超时···
看个例子
比如计算
2*2*2*2*2*2*2*2*2*2*2
可以这样算
原式=4*4*4*4*4*2
=8*8*4*2
=16*4*2
你看,相同的可以先合并,减少计算步骤
a^b mod c = (a mod c)^c mod c
如果题目说数据很大,还需要求余,那么递归代码就可以这么写:/ / 有的时候题目要求求余,没要求就不用求余数了
1 LL pow_mod(LL a, LL b){ //a的b次方 2 if(b == 0) return 1; 3 LL ret = pow_mod(a, b/2); 4 ret = ret * ret % MOD; 5 if(b % 2 == 1) ret = ret * a % MOD; 6 return ret; 7 }
递推:
1 LL pow_mod(LL a, LL b){ //a的b次方 2 LL ret = 1; 3 while(b != 0){ 4 if(b % 2 == 1){ 5 ret = (ret * a) % MOD ; 6 } 7 a = (a * a ) % MOD ; 8 b /= 2; 9 } 10 return ret; 11 }
位运算形式:(速度又快,又好理解,在加一个求余p
1 LL pow_mod(LL a, LL b, LL p){//a的b次方求余p 2 LL ret = 1; 3 while(b){ 4 if(b & 1) ret = (ret * a) % p; 5 a = (a * a) % p; 6 b >>= 1; 7 } 8 return ret; 9 }
学习Rabin-Miller算法的时候我们为了防止求的时候溢出,通常会使用一种叫做“快速乘”的算法。不得不承认我第一次见到这东西的时候确实是一脸懵逼的,下面我们来用之前的知识学习一下这个算法。
(请先忘记)
现在我们的任务是:
用O(log(b))次加法计算a*b%mod(因为直接计算a*b会溢出,而我们保证加法不会溢出)
例如:
注意到一个小学生级别的事实:
所以我们可以把看成a的b次幂
现在我们check一下这个新的“幂运算”是否满足上面提到的3个条件
封闭性显然满足
结合律满足
- 单位元为0
全部都满足呢!Y(^o^)Y
所以我们把上面的代码中的乘法改成加法就大功告成啦(当然单位元也是要改的233)!
有了快速幂,于是,快速乘诞生了:
1 ll fastMultiplication(ll a,ll b,ll mod){ 2 ll ans = 0; 3 while(b){ 4 if(b%2==1){ 5 b--; 6 ans = ans + a; 7 ans %= mod; 8 }else{ 9 b /= 2; 10 a = a + a; 11 a %= mod; 12 } 13 } 14 return ans; 15 }
1 LL mul(LL a, LL b, LL p){//快速乘,计算a*b%p 2 LL ret = 0; 3 while(b){ 4 if(b & 1) ret = (ret + a) % p; 5 a = (a + a) % p; 6 b >>= 1; 7 } 8 return ret; 9 }
1 ll fastExp(ll a,ll k){ //快速幂2 2 ll ans = 1; 3 while(k){ 4 if(k%2==1){ 5 k--; 6 ans = ans * a; 7 }else{ 8 a = a * a; 9 k/=2; 10 } 11 } 12 return ans; 13 }
快速幂用到了什么性质
- “乘法”满足封闭性
- “乘法”满足结合律
- “乘法”下有单位元(其实这条不一定要,因为可以初始化ans到a(不过anyway我们假设一开始是单位元吧
1 #include <iostream>//实例代码 2 using namespace std; 3 int quickPow(int a,int b){ //快速幂 4 int ans = 1; 5 while(b){ 6 if(b&1) ans*=a; 7 a *= a; 8 b /= 2; 9 } 10 return ans; 11 } 12 int pow(int a,int b){ //普通乘 13 int ans = 1; 14 for(int i=1; i<=b; i++) 15 ans *= a; 16 return ans; 17 } 18 int main(int argc, const char * argv[]) { 19 cout<<quickPow(2, 20)<<endl; //第一种方式 20 cout<<pow(2,20)<<endl; //第二种方式 21 return 0; 22 } 23 24 作者:徐森威 25 链接:http://www.jianshu.com/p/1c3f88f63dec 26 來源:简书 27 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
while(b){ //快速幂核心代码 if(b&1) ans*=a; a *= a; b /= 2; }上面的两种方式,一种复杂度是
O(logn),一种复杂度是O(n)。当你数量级很大的时候,比如10000000000时,这个复杂度的时间差别就很大了怎么得到这个快速幂的代码的呢?我们假设需要求274
74转化为二进制为1001010,根据二进制对应位的1,可以把74拆分为64+8+2 ,所以
74 = 26 + 23 + 21
274 = 226 + 223 + 221while(b){ //快速幂核心代码 if(b&1) ans*=a; a *= a; b /= 2; }下面看一下上面这段快速幂程序中的ans和a的用法 (74二进制1001010为从右到左下面表格从1-7)
初始值 0 1(ans变了) 0 1(ans变了) 0 0 1(ans变了) a = 2n 21 22 24 28 216 232 264 2128 ans 20 20 20×22 20×22 20×22×28 20×22×28 20×22×28 20×22×28×264 这里有两个变量,第一个变量
a默认用来存2n,,变量ans存储的是最后的结果,当遇到第k位的二进制位是1的时候,则ans ×= 2k举个例子,74的二进制表示是
1001010,因为是除2运算,所以从右往左遍历,到右边第二个时,ans ×= 22,到右边第四个时,ans ×= 28,到右边第7个时,ans ×= 264,最后ans = 274,至于ans乘的过程中的那些22、28、264怎么来?a变量不是一直在不断增加吗,ans乘的就是a变量对应位的值,对应上面的表格可能看的更清楚一点