RMQ(Range Minimum/Maximum Query)问题是指:对于长度为n的数列A,回答若干询问RMQ(A,i,j),返回数列A中下标i,j里的最小/大值,即RMQ问题是指求区间最值的问题。
时间复杂度:O(N)~ O(logN)
主要思想:分治/倍增/动态规划
主要算法:
1.朴素(暴力搜索)//略过不表
2.线段树
3.ST(Sparse-Table)算法(动态规划)
线段树:线段树能在对数时间logN在数组区间上进行更新与查询。而未优化的空间复杂度为2N,因此有时需要离散化让空间压缩。
线段树是一种二叉搜索树,与区间树相似,将一个区间划分为一些单元区间,每个单元区间对应线段树中的一个叶节点。对于线段树中的每一个非叶子节点[i,j],定义如下:
第一个节点维护区间[i,j]的信息
if i<j,那么左孩子维护区间[i,(i+j)/2]的信息,右孩子维护区间[(i+j)/2+1,j]的信息。
线段树至少支持下列操作:
insert(t,x):将包含区间int的元素x插入到树t中;
delete(t,x):从线段树t中删除元素x;
search(t,i):返回一个指向树t中元素x的指针。
区间在[1,5]内的线段树 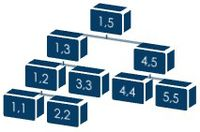
基本结构:
线段树是建立在线段的基础上,每个结点都代表了一条线段[a , b]。长度为1的线段称为元线段。非元线段都有两个子结点,左结点代表的线段为[a , (a + b ) / 2],右结点代表的线段为[( a + b ) / 2 , b]。
右图就是一棵长度范围为[1 , 5]的线段树。
长度范围为[1 , L] 的一棵线段树的深度为log ( L - 1 ) + 1。这个显然,而且存储一棵线段树的空间复杂度为O(L)。
线段树支持最基本的操作为插入和删除一条线段。下面以插入为例,详细叙述,删除类似。
将一条线段[a , b] 插入到代表线段[l , r]的结点p中,如果p不是元线段,那么令mid=(l+r)/2。如果b<mid,那么将线段[a , b] 也插入到p的左儿子结点中,如果a>mid,那么将线段[a , b] 也插入到p的右儿子结点中。
插入(删除)操作的时间复杂度为O (Log N)。
实际应用:
上面的都是些基本的线段树结构,但只有这些并不能做什么,就好比一个程序有输入没输出,根本没有任何用处。
最简单的应用就是记录线段有否被覆盖,并随时查询当前被覆盖线段的总长度。那么此时可以在结点结构中加入一个变量int count;代表当前结点代表的子树中被覆盖的线段长度和。这样就要在插入(删除)当中维护这个count值,于是当前的覆盖总值就是根节点的count值了。
另外也可以将count换成bool cover;支持查找一个结点或线段是否被覆盖。[1]
实际上,通过在结点上记录不同的数据,线段树还可以完成很多不同的任务。例如,如果每次插入操作是在一条线段上每个位置均加k,而查询操作是计算一条线段上的总和,那么在结点上需要记录的值为sum。
这里会遇到一个问题:为了使所有sum值都保持正确,每一次插入操作可能要更新O(N)个sum值,从而使时间复杂度退化为O(N)。
解决方案是Lazy思想:对整个结点进行的操作,先在结点上做标记,而并非真正执行,直到根据查询操作的需要分成两部分。
根据Lazy思想,我们可以在不代表原线段的结点上增加一个值toadd,即为对这个结点,留待以后执行的插入操作k值的总和。对整个结点插入时,只更新sum和toadd值而不向下进行,这样时间复杂度可证明为O(logN)。
对一个toadd值不为0的结点整个进行查询时,直接返回存储在其中的sum值;而若对其一部分进行查询,则要更新其左右子结点的sum值,然后把toadd值传递下去,再对这个查询本身,左右子结点分别递归下去。时间复杂度也是O(logN)。
ST算法:
关于ST算法,实际上它本身并不难,它的思想是动态规划。主要用来求RMQ问题,时间复杂度为O(NlgN+M)
关于RMQ问题描述:
输入N个数和M次询问,每次询问一个区间[L,R],求第L个数到R个数之间的最大值,或者是求最小值。
它的原理阐述如下:
对于一个数组A[0...N-1],我们用f[i][j]表示A[i]到A[i+2^j-1],这个范围内的最大值。
由于此区间的元素个数很明显为2^j个,所以我们又可以从中间平分为两部分,这样每部分又有2^(j-1)个元素,这样我们就知道区间[i,i+2^j-1]可以分为[i,i+2^(j-1)-1]和[i+2^(j-1),i+2^j-1]两部分,我们只需要求出后面两个区间最大值的较大值,就可以知道前面区间的最大值了。
所以到了这里,很明显可以写出状态转移方程:
f[i][j]=max(f[i][j-1],f[i+2^(j-1)][j-1])
当然很明显知道初始化f[i][0]=A[i]
当然上面i,j的范围是多少呢?
现在我们来分析一下:我们已经说了如果用上述原理一个区间的元素是2^j个,而可以知道2^j<=N的,所以这样就得到j<=log(N)/log(2); 当然j还大于等于1
对于i,就直接有i+2^j-1<N就行了。
到了这里,我们就可以把f[i][j]求出来了。
接下来就是query()了。
这个怎么办呢,其实很容易,我们先求出满足条件2^x=R-L+1的最大x
这样我们我们就可以把区间[L,R]求最值问题转化为了求区间[L,L+2^x-1]和区间[R-2^x+1,R]最大值的较大值了,为什么可以这样做,因为这两个区间中间有重叠。
但是这两个区间的并一定等于区间[L,R],所以到了这里ST算法的原理基本常阐述完毕了。
剩下的就是代码实现了。

#include <stdio.h> #include <math.h> #define N 1005 int m,n; int a[N]; int f[N][N]; int max(int a,int b) { return a>b? a:b; } void ST() { int i,j; for(i=0;i<n;i++) f[i][0]=a[i]; for(j=1;j<=(int)((log((double)n)/log(2.0)));j++) { for(i=0;i+(1<<j)-1<n;i++) f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); } } int query(int L,int R) { int x=(int)(log((double)(R-L+1))/log(2.0)); return max(f[L][x],f[R-(1<<x)+1][x]); } int main() { int i,L,R; while(~scanf("%d%d",&n,&m)) { for(i=0;i<n;i++) scanf("%d",&a[i]); ST(); while(m--) { scanf("%d%d",&L,&R); printf("%d ",query(L-1,R-1)); } } return 0; }
