题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数加上x
2.求出某区间每一个数的和
输入格式
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式
输出包含若干行整数,即为所有操作2的结果。
输入输出样例
输入 #1
5 5 1 5 4 2 3 2 2 4 1 2 3 2 2 3 4 1 1 5 1 2 1 4
输出 #1
11 8 20
说明/提示
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=1000,M<=10000
对于100%的数据:N<=100000,M<=100000
(数据已经过加强^_^,保证在int64/long long数据范围内)
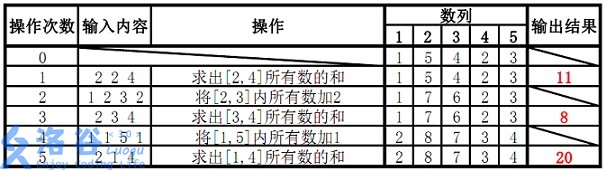
样例说明:
#include <cstdio> #include <iostream> #include <cmath> #include <string> #include <cstring> #include <algorithm> #include <queue> #include <vector> #include <map> using namespace std; #define ll long long #define eps 1e-9 const int inf = 0x3f3f3f3f; const int mod = 1e9+7; ll n, m, a[1000000+8], ans; struct node { ll left, right, sum, lz; }tree[1000000+8]; void build(ll left, ll right, ll i)///建树 { tree[i].lz = 0;///懒惰标记初始化为0 tree[i].left = left; tree[i].right = right; if(left == right)///如果已经是叶子结点 { tree[i].sum = a[left]; return ; } ll mid = (right+left)/2; build(left, mid, i*2);///往左边的区间进行建树 build(mid+1, right, i*2+1);///往右边的区间进行建树 tree[i].sum = tree[i*2].sum+tree[i*2+1].sum;///自己的和等于左儿子和右儿子的和 } void push_down(ll i)///把自己的lazytage归零,并给自己的儿子加上,并让自己的儿子加上k*(r-l+1) { if(tree[i].lz != 0)///如果这个点已经被标记了 { tree[i*2].lz += tree[i].lz;///左儿子的懒惰标记等于父亲的懒惰标记 tree[i*2+1].lz += tree[i].lz;///右儿子的懒惰标记等于父亲的懒惰标记 ll mid = (tree[i].left+tree[i].right)/2; tree[i*2].sum += tree[i].lz*(mid-tree[i*2].left +1);///左儿子的和等于它所控制的区间的和 tree[i*2+1].sum += tree[i].lz*(tree[i*2+1].right-mid);///右儿子的和等于它所控制的区间的和 tree[i].lz = 0;///父节点懒惰标记归零 } return ; } void pls(ll i, ll l, ll r, ll k)///区间加 { if(tree[i].right <= r && tree[i].left >= l)///如果这个区间就在目标区间的内部 { tree[i].sum += k*(tree[i].right-tree[i].left+1);///这个区间的和 等于(这个区间原本的和)+(k*这个区间的元素个数) tree[i].lz += k;///懒惰标记,表示它已经加了k return ; } push_down(i);///把自己的lazytage归零,并给自己的儿子加上,并让自己的儿子加上k*(r-l+1) if(tree[i*2].right >= l)///如果这个区间与左边部分区间重叠,就往左边区间每个元素加上k pls(i*2, l, r, k); if(tree[i*2+1].left <= r)///如果这个区间与右边部分区间重叠,就往右边区间每个元素加上k pls(i*2+1, l, r, k); tree[i].sum = tree[i*2].sum+tree[i*2+1].sum;///父节点的和等于左儿子的和加右儿子的和 return ; } void search(ll i, ll l, ll r)///查找区间和 { if(tree[i].left >= l && tree[i].right <= r)///如果这个区间就在目标区间的内部 { ans += tree[i].sum; return ; } if(tree[i].lz) push_down(i);///一层一层的进行标记,方便后来的查找区间和 ll mid = (tree[i].left+tree[i].right)/2; if(l <= mid)///如果这个区间与左边部分区间重叠,就 ans + 左边区间每个元素加上k search(i*2, l, r); if(mid<r)///如果这个区间与右边部分区间重叠,就 ans + 右边区间每个元素加上k search(i*2+1, l, r); } int main() { scanf("%lld%lld", &n, &m); for(ll i = 1; i <= n; i++)scanf("%lld", &a[i]); build(1, n, 1);///初始化线段树 for(ll i = 1; i <= m; i++) { ll f; scanf("%lld", &f); if(f == 1) { ll x, y, z; scanf("%lld%lld%lld", &x, &y, &z); pls(1, x, y, z);///从根节点开始进行区间加c } else if(f == 2) { ll x, y; scanf("%lld%lld", &x, &y); ans = 0; search(1, x, y); printf("%lld ", ans);///输出区间[a, b]的值 } } return 0; }