应用深度学习EEGNet来处理脑电信号

本分享为脑机学习者Rose整理发表于公众号：脑机接口社区(微信号：Brain_Computer).QQ交流群：903290195

EEGNet论文

EEGNet简介

脑机接口(BCI)使用神经活动作为控制信号，实现与计算机的直接通信。这种神经信号通常是从各种研究透彻的脑电图(EEG)信号中挑选出来的。卷积神经网络(CNN)主要用来自动特征提取和分类，其在计算机视觉和语音识别领域中的使用已经很广泛。CNN已成功应用于基于EEG的BCI；但是，CNN主要应用于单个BCI范式，在其他范式中的使用比较少，论文作者提出是否可以设计一个CNN架构来准确分类来自不同BCI范式的EEG信号，同时尽可能地紧凑(定义为模型中的参数数量)。该论文介绍了EEGNet，这是一种用于基于EEG的BCI的紧凑型卷积神经网络。论文介绍了使用深度和可分离卷积来构建特定于EEG的模型，该模型封装了脑机接口中常见的EEG特征提取概念。论文通过四种BCI范式(P300视觉诱发电位、错误相关负性反应(ERN)、运动相关皮层电位(MRCP)和感觉运动节律(SMR))，将EEGNet在主体内和跨主体分类方面与目前最先进的方法进行了比较。结果显示，在训练数据有限的情况下，EEGNet比参考算法具有更强的泛化能力和更高的性能。同时论文也证明了EEGNet可以有效地推广到ERP和基于振荡的BCI。
网络结构图如下：

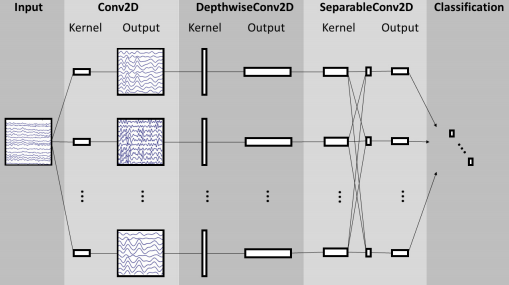
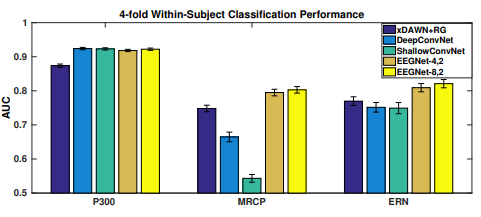
实验结果如下图，P300数据集的所有CNN模型之间的差异非常小，但是MRCP数据集却存在显著的差异，两个EEGNet模型的性能都优于所有其他模型。对于ERN数据集来说，两个EEGNet模型的性能都优于其他所有模型(p < 0.05)。

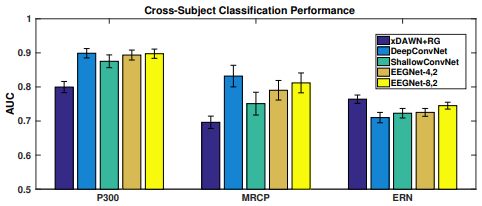
如下图每个模型的P300，ERN和MRCP数据集的分类性能平均为30倍。对于P300和MRCP数据集，DeepConvNet和EEGNet模型之间的差异很小，两个模型的性能均优于ShallowConvNet。对于ERN数据集，参考算法（xDAWN + RG）明显优于所有其他模型。

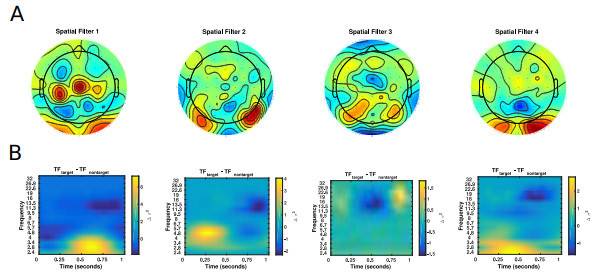
下图是对EEGNet-4,1模型配置获得的特征进行可视化，
（A）每个空间过滤器的空间拓扑。
（B）每个滤波器的目标试验和非目标试验之间的平均小波时频差。

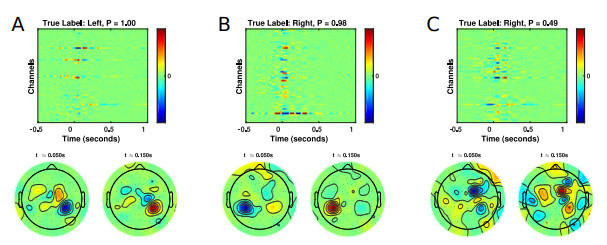
下图中第一排是使用DeepLIFT针对MRCP数据集的三个不同测试试验，对使用cross-subject训练的EEGNet-8,2模型进行的单次试验脑电特征相关性：
（A）高可信度，正确预测左手运动;
（B）高可信度，正确预测右手运动;
（C）低可信度，错误预测左手运动。
标题包括真实的类别标签和该标签的预测概率。

第二排是在两个时间点的相关性空间分布图：按钮按下后大约50毫秒和150毫秒。与预期的一样，高可信度试验显示出分别对应左（A）和右（B）按钮对应的对侧运动皮层的正确相关性。对于低置信度的试验，可以看到相关性更加混杂且分布广泛，而运动皮质没有明确的空间定位。

EEGNet代码实现

作者提供的代码用的是旧版本的Pytorch，所以有一些错误。Rose小哥基于作者提供的代码在Pytorch 1.3.1(only cpu)版本下修改，经测试，在Rose小哥环境下可以运行[不排除在其他环境可能会存在不兼容的问题]

# 导入工具包
import numpy as np
from sklearn.metrics import roc_auc_score, precision_score, recall_score, accuracy_score
import torch
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
import torch.nn.functional as F
import torch.optim as optim

EEGNet网络模型参数如下：

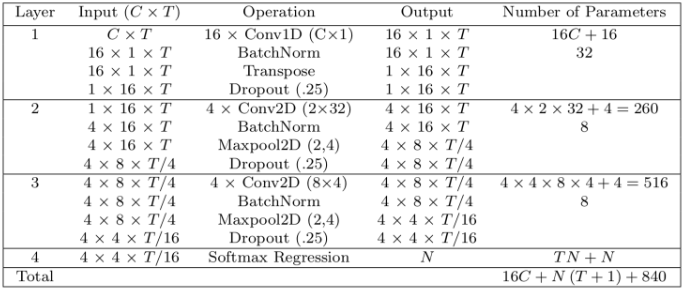
定义网络模型：

class EEGNet(nn.Module):
    def __init__(self):
        super(EEGNet, self).__init__()
        self.T = 120

        # Layer 1
        self.conv1 = nn.Conv2d(1, 16, (1, 64), padding = 0)
        self.batchnorm1 = nn.BatchNorm2d(16, False)

        # Layer 2
        self.padding1 = nn.ZeroPad2d((16, 17, 0, 1))
        self.conv2 = nn.Conv2d(1, 4, (2, 32))
        self.batchnorm2 = nn.BatchNorm2d(4, False)
        self.pooling2 = nn.MaxPool2d(2, 4)

        # Layer 3
        self.padding2 = nn.ZeroPad2d((2, 1, 4, 3))
        self.conv3 = nn.Conv2d(4, 4, (8, 4))
        self.batchnorm3 = nn.BatchNorm2d(4, False)
        self.pooling3 = nn.MaxPool2d((2, 4))

        # 全连接层
        # 此维度将取决于数据中每个样本的时间戳数。
        # I have 120 timepoints. 
        self.fc1 = nn.Linear(4*2*7, 1)


    def forward(self, x):
        # Layer 1
        x = F.elu(self.conv1(x))
        x = self.batchnorm1(x)
        x = F.dropout(x, 0.25)
        x = x.permute(0, 3, 1, 2)

        # Layer 2
        x = self.padding1(x)
        x = F.elu(self.conv2(x))
        x = self.batchnorm2(x)
        x = F.dropout(x, 0.25)
        x = self.pooling2(x)

        # Layer 3
        x = self.padding2(x)
        x = F.elu(self.conv3(x))
        x = self.batchnorm3(x)
        x = F.dropout(x, 0.25)
        x = self.pooling3(x)

        # 全连接层
        x = x.view(-1, 4*2*7)
        x = F.sigmoid(self.fc1(x))
        return x

定义评估指标：
acc：准确率
auc:AUC 即 ROC 曲线对应的面积
recall:召回率
precision:精确率
fmeasure：F值

def evaluate(model, X, Y, params = ["acc"]):
    results = []
    batch_size = 100

    predicted = []

    for i in range(len(X)//batch_size):
        s = i*batch_size
        e = i*batch_size+batch_size

        inputs = Variable(torch.from_numpy(X[s:e]))
        pred = model(inputs)

        predicted.append(pred.data.cpu().numpy())

    inputs = Variable(torch.from_numpy(X))
    predicted = model(inputs)
    predicted = predicted.data.cpu().numpy()
    """
    设置评估指标：
    acc：准确率
    auc:AUC 即 ROC 曲线对应的面积
    recall:召回率
    precision:精确率
    fmeasure：F值
    """
    for param in params:
        if param == 'acc':
            results.append(accuracy_score(Y, np.round(predicted)))
        if param == "auc":
            results.append(roc_auc_score(Y, predicted))
        if param == "recall":
            results.append(recall_score(Y, np.round(predicted)))
        if param == "precision":
            results.append(precision_score(Y, np.round(predicted)))
        if param == "fmeasure":
            precision = precision_score(Y, np.round(predicted))
            recall = recall_score(Y, np.round(predicted))
            results.append(2*precision*recall/ (precision+recall))
    return results

构建网络EEGNet，并设置二分类交叉熵和Adam优化器

# 定义网络
net = EEGNet()
# 定义二分类交叉熵 (Binary Cross Entropy)
criterion = nn.BCELoss()
# 定义Adam优化器
optimizer = optim.Adam(net.parameters())

创建数据集

"""
生成训练数据集，数据集有100个样本
训练数据X_train:为[0,1)之间的随机数;
标签数据y_train:为0或1
"""
X_train = np.random.rand(100, 1, 120, 64).astype('float32')
y_train = np.round(np.random.rand(100).astype('float32')) 
"""
生成验证数据集，数据集有100个样本
验证数据X_val:为[0,1)之间的随机数;
标签数据y_val:为0或1
"""
X_val = np.random.rand(100, 1, 120, 64).astype('float32')
y_val = np.round(np.random.rand(100).astype('float32'))
"""
生成测试数据集，数据集有100个样本
测试数据X_test:为[0,1)之间的随机数;
标签数据y_test:为0或1
"""
X_test = np.random.rand(100, 1, 120, 64).astype('float32')
y_test = np.round(np.random.rand(100).astype('float32'))

训练并验证

batch_size = 32
# 训练 循环
for epoch in range(10): 
    print("
Epoch ", epoch)

    running_loss = 0.0
    for i in range(len(X_train)//batch_size-1):
        s = i*batch_size
        e = i*batch_size+batch_size

        inputs = torch.from_numpy(X_train[s:e])
        labels = torch.FloatTensor(np.array([y_train[s:e]]).T*1.0)

        # wrap them in Variable
        inputs, labels = Variable(inputs), Variable(labels)

        # zero the parameter gradients
        optimizer.zero_grad()

        # forward + backward + optimize
        outputs = net(inputs)
        loss = criterion(outputs, labels)
        loss.backward()

        optimizer.step()

        running_loss += loss.item()

    # 验证
    params = ["acc", "auc", "fmeasure"]
    print(params)
    print("Training Loss ", running_loss)
    print("Train - ", evaluate(net, X_train, y_train, params))
    print("Validation - ", evaluate(net, X_val, y_val, params))
    print("Test - ", evaluate(net, X_test, y_test, params))

Epoch 0
['acc', 'auc', 'fmeasure']
Training Loss 1.6107637286186218
Train - [0.52, 0.5280448717948718, 0.6470588235294118]
Validation - [0.55, 0.450328407224959, 0.693877551020408]
Test - [0.54, 0.578926282051282, 0.6617647058823529]

Epoch 1
['acc', 'auc', 'fmeasure']
Training Loss 1.5536684393882751
Train - [0.45, 0.41145833333333337, 0.5454545454545454]
Validation - [0.55, 0.4823481116584565, 0.6564885496183207]
Test - [0.65, 0.6530448717948717, 0.7107438016528926]

Epoch 2
['acc', 'auc', 'fmeasure']
Training Loss 1.5197088718414307
Train - [0.49, 0.5524839743589743, 0.5565217391304348]
Validation - [0.53, 0.5870279146141215, 0.5436893203883495]
Test - [0.57, 0.5428685897435898, 0.5567010309278351]

Epoch 3
['acc', 'auc', 'fmeasure']
Training Loss 1.4534167051315308
Train - [0.53, 0.5228365384615385, 0.4597701149425287]
Validation - [0.5, 0.48152709359605916, 0.46808510638297873]
Test - [0.61, 0.6502403846153847, 0.5517241379310345]

Epoch 4
['acc', 'auc', 'fmeasure']
Training Loss 1.3821702003479004
Train - [0.46, 0.4651442307692308, 0.3076923076923077]
Validation - [0.47, 0.5977011494252874, 0.29333333333333333]
Test - [0.52, 0.5268429487179488, 0.35135135135135137]

Epoch 5
['acc', 'auc', 'fmeasure']
Training Loss 1.440490186214447
Train - [0.56, 0.516025641025641, 0.35294117647058826]
Validation - [0.36, 0.3801313628899836, 0.2]
Test - [0.53, 0.6113782051282052, 0.27692307692307694]

Epoch 6
['acc', 'auc', 'fmeasure']
Training Loss 1.4722238183021545
Train - [0.47, 0.4194711538461539, 0.13114754098360656]
Validation - [0.46, 0.5648604269293925, 0.2285714285714286]
Test - [0.5, 0.5348557692307693, 0.10714285714285714]

Epoch 7
['acc', 'auc', 'fmeasure']
Training Loss 1.3460421562194824
Train - [0.51, 0.44871794871794873, 0.1694915254237288]
Validation - [0.44, 0.4490968801313629, 0.2]
Test - [0.53, 0.4803685897435898, 0.14545454545454545]

Epoch 8
['acc', 'auc', 'fmeasure']
Training Loss 1.3336675763130188
Train - [0.54, 0.4130608974358974, 0.20689655172413793]
Validation - [0.39, 0.40394088669950734, 0.14084507042253522]
Test - [0.51, 0.5400641025641025, 0.19672131147540983]

Epoch 9
['acc', 'auc', 'fmeasure']
Training Loss 1.438510239124298
Train - [0.53, 0.5392628205128205, 0.22950819672131148]
Validation - [0.42, 0.4848111658456486, 0.09375]
Test - [0.56, 0.5420673076923076, 0.2413793103448276]

参考
应用深度学习EEGNet来处理脑电信号

本文章由脑机学习者Rose笔记分享,QQ交流群：903290195
更多分享，请关注公众号