树的直径学习笔记

概念/定义

树上最长简单路径即为树的直径.

算法

两次 DFS

时间复杂度: (O (n))

• 做法:

  1. 在树上任取一点, 通过一遍 DFS 找到距离其最远点 (X).
  2. 从 (X) 进行第二遍 DFS 找到距离其最远点 (Z).
  3. (X-Z) 路径即为树的直径.

• 正确性证明:

  采用反证法. 假设 (X-Z) 不为直径, 而是存在 (A-C > X-Z).

  1. 当 (X-Z) 与 (A - C) 交于一点 (Y) 时,

     
     如图所示, (Y) 为交点.

     因为 (Z) 为距 (X) 的最远点, 所以有:

     (XY + YZ > XY + YC)

     (=> YZ > YC)

     (=> AY + YZ > AY + YC)

     (=> A - Z > A - C)

     所以 (A - C) 不为直径, 假设不成立.

  2. 当 (X - Z) 与 (A - C) 无交点时,

     
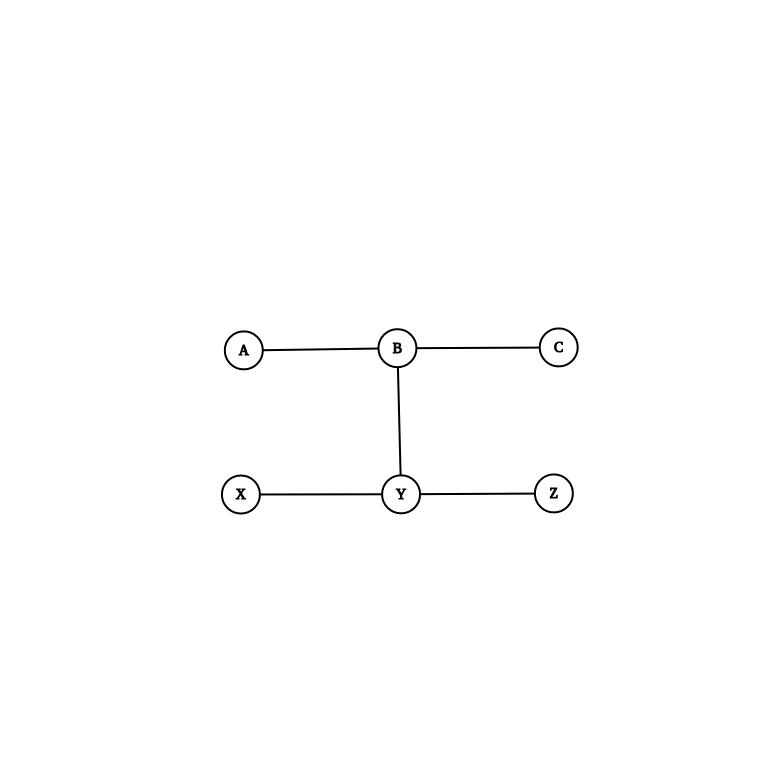
     如图所示. (B) 为 (A - C) 上任意一点, (Y) 为 (X - Z) 上任意一点.

     因为 (Z) 为距 (X) 最远点, 所以有:

     (XY + YZ > XY + YB + BC)

     (=> YZ > YB + BC)

     (=> YZ + YB > 2 * YB + BC)

     (=> AB + YZ + YB > AB + BC + 2 * YB)

     (=> A - Z > A - C + 2 * YB)

     (2 * YB > 0 => A - Z > A - C)

     所以 (A - C) 不为直径, 假设不成立.

  综上, (X - Z) 是直径.

树形 DP

时间复杂度: (O (n))

• 做法:

  1. 状态设立:

     设 (F (i)) 表示以 (i) 为根的子树中的最长路径, (G(i)) 表示以 (i) 为根的子树中的次长路径.

  2. 转移:

     (F(i)) 与 (G(i)) 表示路径是不能有交的, 因此应由不同子树进行转移.

     考虑遍历每一棵子树 (j):

     • 当 (F (j) + 1 > F(i)) 时, (G(i) = F(i)) 且 (F(i) = F(j) + 1)
     • 当 (G(i) < F(j) + 1 < F(i)) 时, (G(i) = F(j) + 1)

  3. 统计答案:

     (Ans = max ( F(i) + G(i) ))

• 正确性证明:

  1. 结论: 树的直径的端点一定是叶子结点 (无根树).

     证明: 反证法.

     假设树的直径为 (A - B) 且 (A) 不为叶子结点.

     那么肯定 (A) 的度数 (k geq 2) 即 (A) 至少有两条边关联.

     只要走那条不在 (A - B) 上的边就能得到了新的直径 (A - C = A - B + 1).

     所以假设不成立, 结论得证.

  2. (F (i)) 和 (G(i)) 都是由叶子结点转移过来的, 由上方结论可知做法的正确性成立.

其他性质

1. 连接两棵树 (X) 与 (Y) 中的两点, 新树 (Z) 的直径的端点一定 为 (X) 与 (Y) 直径的四个端点中的两个.

   证明:

   

   如图所示.

   考虑新树的直径的组成方案:

   1. (X) 中直径. (符合性质)

   2. (Y) 中直径. (符合性质)

   3. 横跨 (U V):

      设 (U) 在 (X) 中距离最远点为 (A), (V) 在 (Y) 中距离最远点为 (B).

      那么横跨 (U V) 的最长路径就是 (A - U + U V + V - B). 根据两次 DFS 求直径的方法可知, (A,B) 均为直径端点.