线性回归
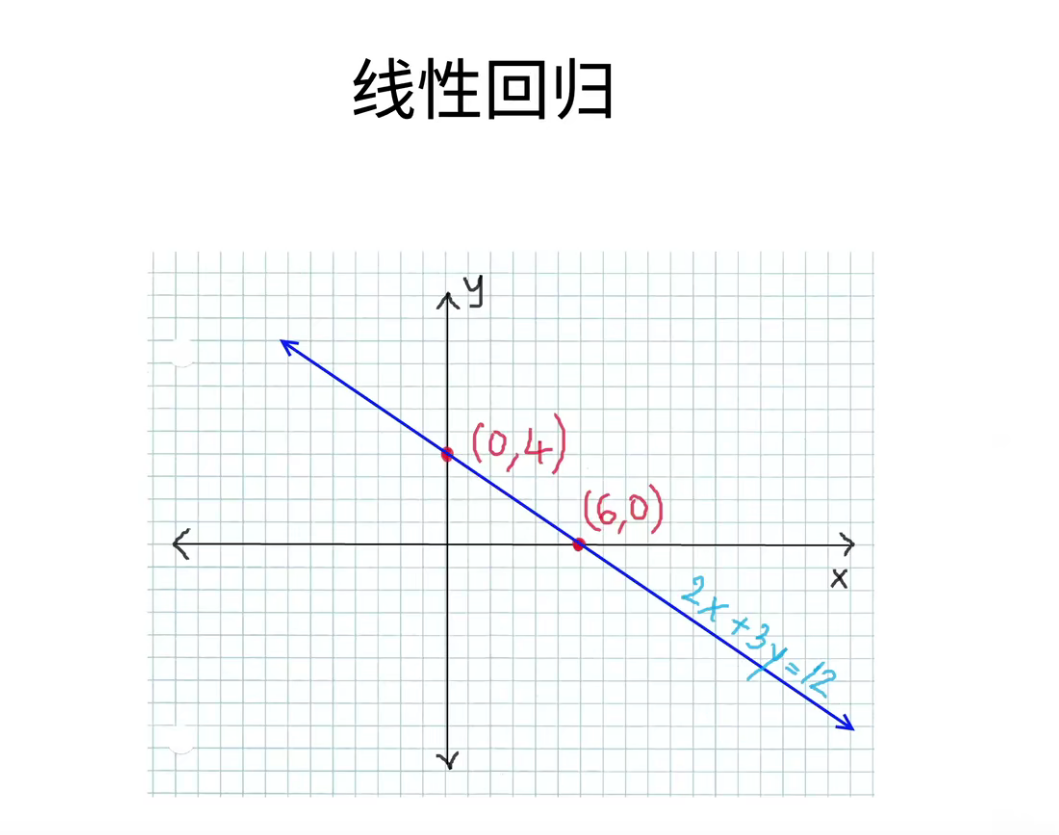
线性回归是机器学习中最基础的模型,也是后面我们理解所有模型的一个基础。




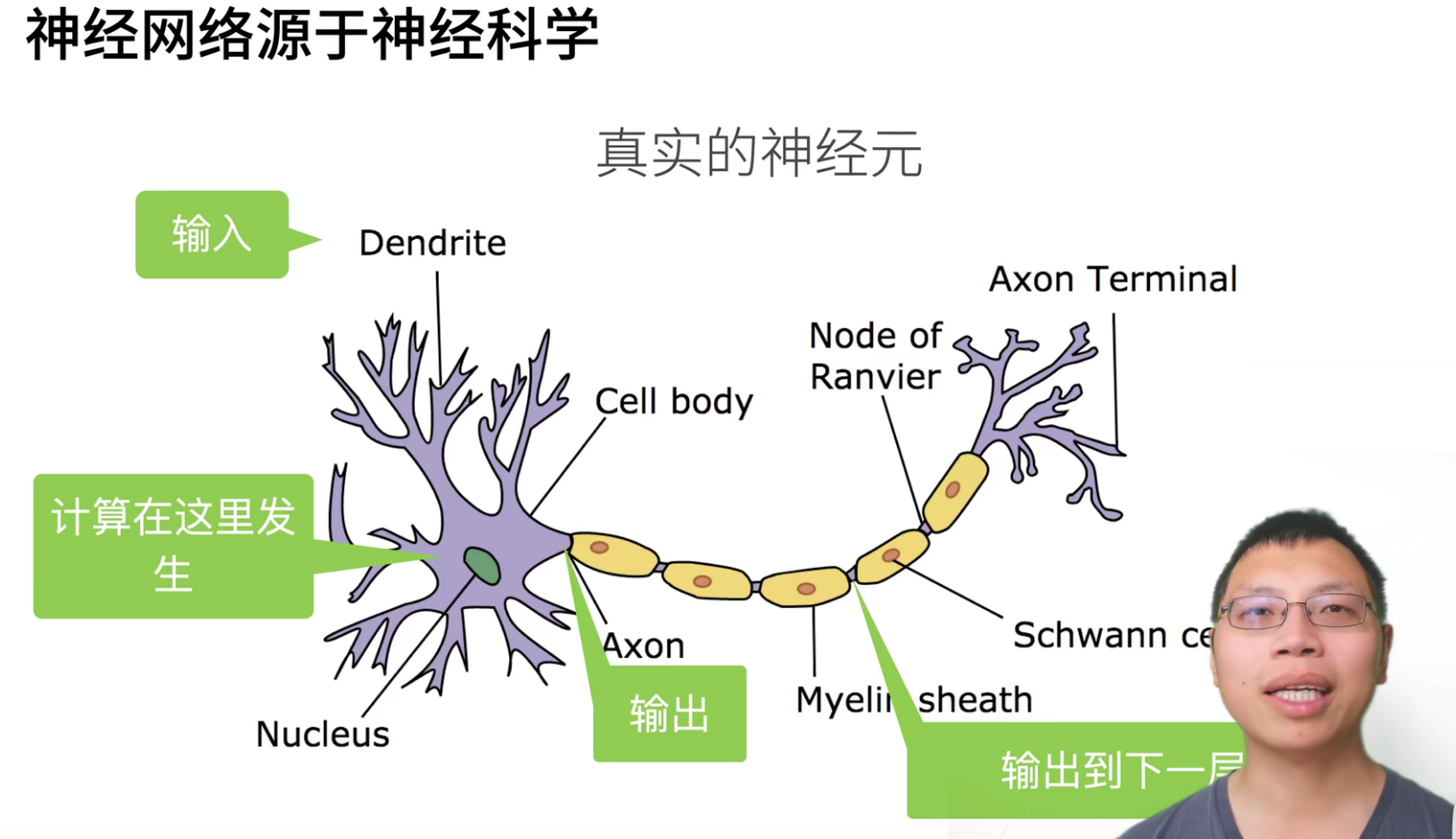
之所以在深度学习中讲解线性模型,是因为它可以看作是一个单层神经网络(输出层可以不看做一个层,将权重和输入层看作一层)。


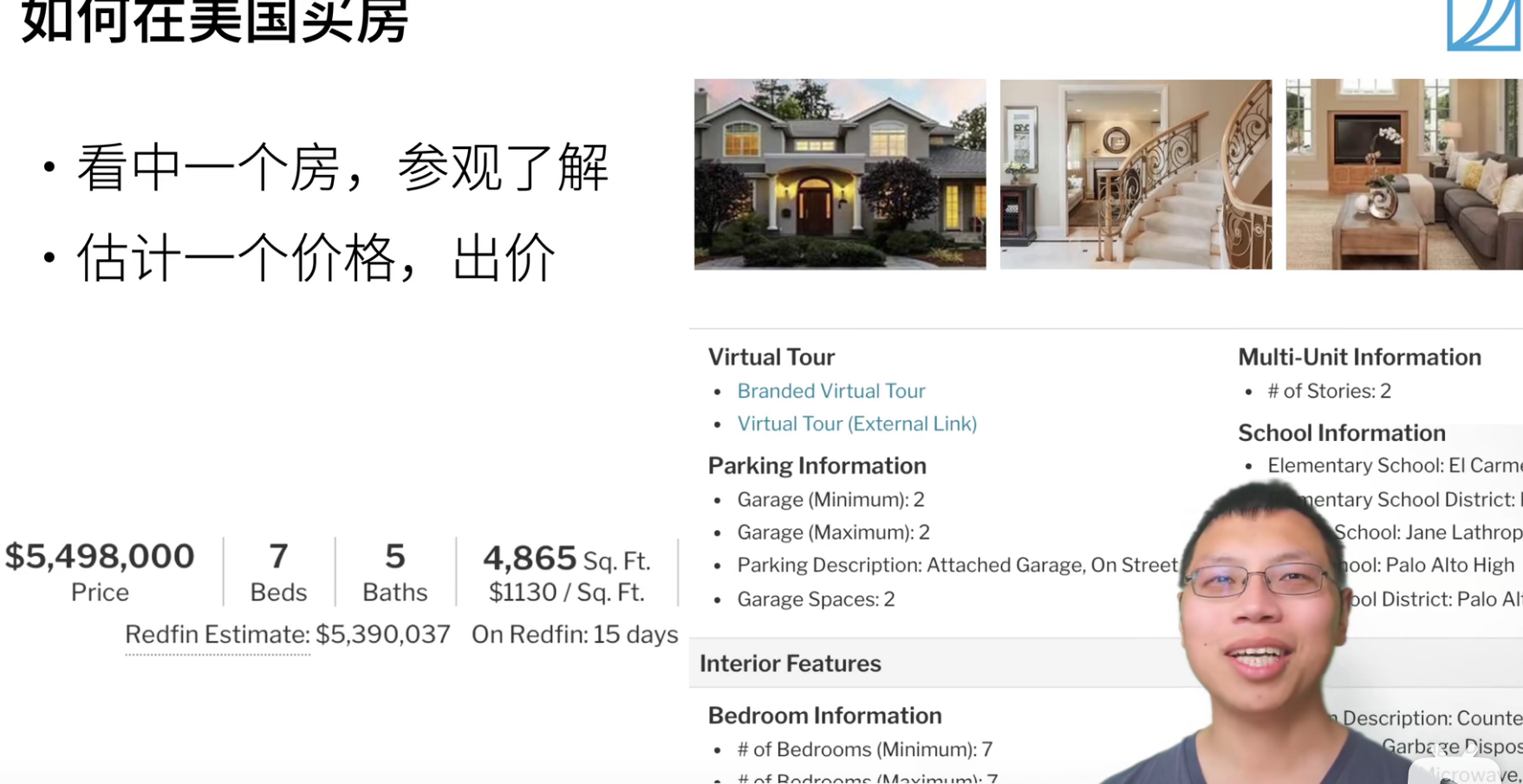
训练数据当然是越多越好,但是也会受限于很多事情,房子售卖数据非常有限。所有我们有很多技术来处理,当你的数据不够的时候怎么办?之后会有非常多的算法来探讨这个问题。

评估模型在每个数据上的损失,求均值,就可以得到损失函数的一个结果。
上面损失函数采用的均方误差,也就是第二范数。
最小化损失来学习参数:我们的目标就是找到一个(w,b)是的 (argmin_{loss}(X,y,w,b))。

当然因为是线性模型,所有是有显示解的(就是可以直接求解)。
当然线性方程也是唯一一个有最优解的模型,后面的模型都不会有最优解了。

基础优化算法


当一个模型没有显示解的时候,应该怎么办呢?首先会挑选一个参数的随机初始值,记作(w_0),然后随后不断地去更新(w_0),去接近我们的最优解。
(w_{t-1}):之前的参数,(eta):之前的参数。
我们来直观理解一下,这是一个二次函数的等高线,黄线方向就是负梯度方向。
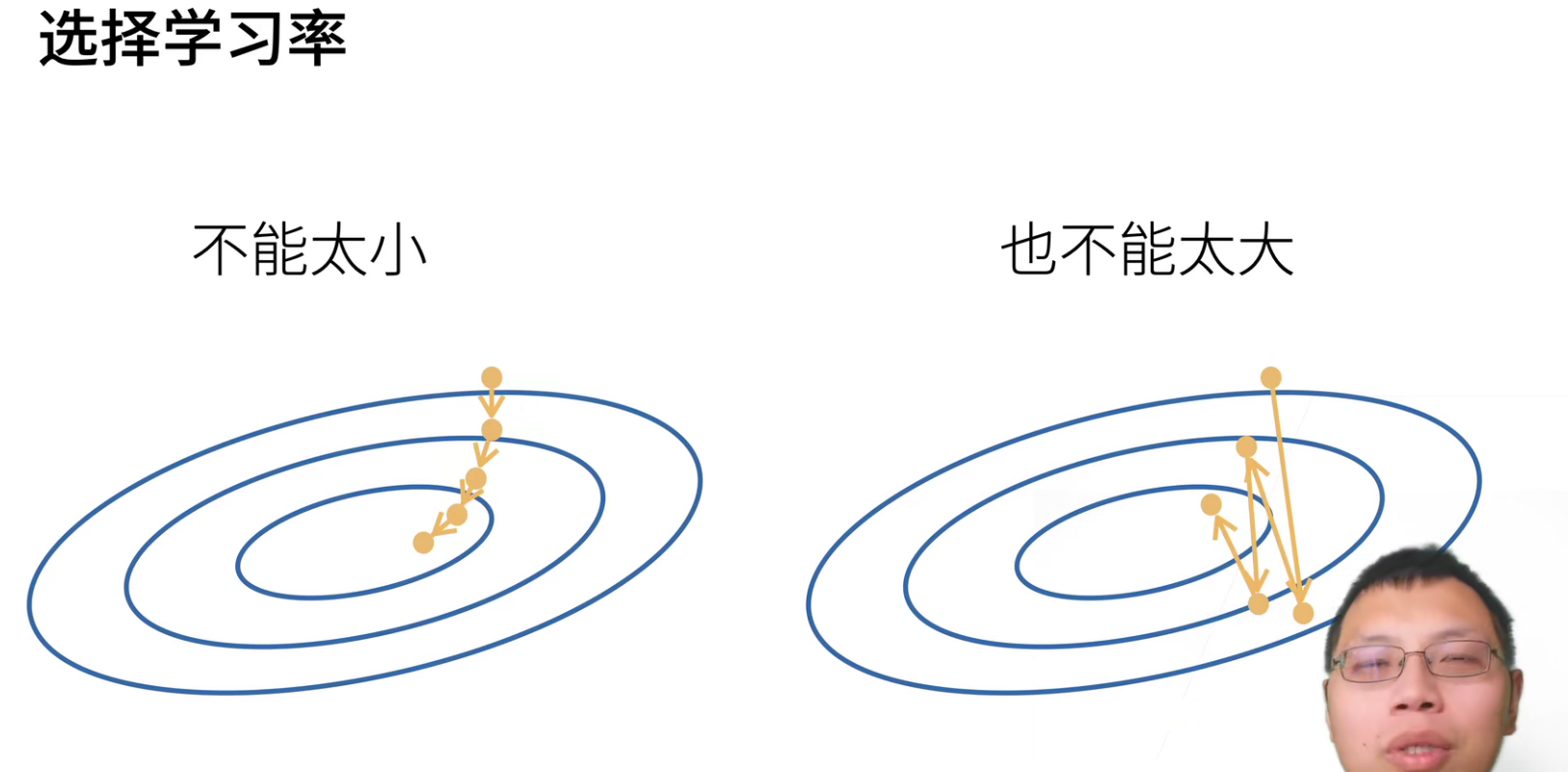
学习率不能太小,太小的话会要“走很多步”,计算梯度是一件很贵的事情。
学习率太大的话,会一直震荡。
学习率不能太大,也不能太小,后面会有一系列的教程,教大家如何选择学习率。

深度学习一般都是使用小批量随机梯度下降。
每次计算梯度,我们要对损失函数求导,损失函数是对我们所有样本的一个平均损失,所以意味着求一次梯度,我们要把所有的样本重新计算一遍,这是很贵的一件事情,计算一次可能需要几个小时,我们训练过程可能有几百步,几千步的样子,这样的话代价太大了。
那么一个近似的办法怎么做呢?我们近似的话,我们可以随机采用b个样本,用它的平均,来近似整个样本的平均。当b很大的时候,近似的比较精确,当b比较小的时候,近似的不那么精确。b比较小的话,计算是比较容易的,因为计算复杂度和样本数量是线性相关的。所以b是批量大小,是另外一个重要的超参数。

同样的,批量大小不能太大,也不能太小。
太小,每次计算都是几个样本的梯度,很难以并行,之后我们会利用GPU来计算,GPU的话动不动就几百上千个核,如果批量太小,那么就不能很好的利用GPU。
太大,内存和批量大小是成正比的,特别是用GPU的话,内存是一个很大的瓶颈。还有一个极端的例子,如果样本太大,有很多相似的样本,其实这就是浪费了计算。
后面也会教大家如何计算这个批量的大小。

梯度下降就是不断沿着梯度的反方向来进行模型的求解,它的好处就是不用知道显示解是什么样子,我只要知道不断的怎么求导数就行了。
小批量随机梯度下降是深度学习默认的求解方法,虽然还有更好的,但是一般来说,它是最稳定的,也是最简单的,所以我们通常使用它。其中批量大小和学习率是两个非常重要的超参数。
当然优化算法是一个非常大的方向,后面会在讨论,当然这个小批量随机梯度下降算法已经够后面用几个星期了。
线性回归的从零开始实现
所谓的从零开始实现,就是我们不使用任何的深度学习框架,而且只使用一些最简单的在tensor上面的计算,这样的好处是可以帮助大家从底层理解每个模块是如何具体实现的。
当然实际应用中,我们不会真的从零开始,但确实一个很好的教学工具。
操纵总结
# 人工生成数据集
def syntheic_data(w,b,num_examples):
X = torch.normal(0,1,(num_examples,len(w)))
y = torch.manmul(X,w) + b
y += torch.normal(0,0.001,y.shape) # 加入噪声
return X,y.reshape(-1,1)
ture_w = torch.tensor([2,-3.4])
ture_b = 4.2
features,labels = syntheic_data(true_w,true_b,1000)
# 批量读取数据的生成器
def data_iter(batch_size,features,labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) # 打乱下标顺序
for i in range(0,num_examples,batch_size):
batch_indices = torch.tensor(indices[i:min(i+batch_size,num_examples)])
yield features[batch_indices],labels[batch_indices]
# 定义 初始化模型参数
w = torch.normal(0,0.01,size=(2,1),requires_grad=True)
b = torch.zeros(1,requires_grad=True)
# 定义模型
def linreg(X,w,b)
return torch.manmul(X,w)+b
# 定义损失函数
def squared_loss(y_hat,y):
# 这是是没有求平均的
return (y_hat-y.reshape(y_hat.shape))**2 / 2
# 定义优化算法
def sgd(params,lr,batch_size);
with torch.no_grad():
for param in parms:
param -= lr*parm.grad/batch_size
param.grad_zero_()
# 训练过程
lr=0.03
num_epochs = 3
net = linreg
loss = squared_loss
batch_size = 10
for epoch in num_epochs:
for X,y in data_iter(batch_size,features,labels)
l = loss(net(X,w,b),y)
l.sum().backward()
sgd([w,b],lr,batch_size)
with torch.grad():
train_l = loss(net(features,w,b),labels)
print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
线性回归的简洁实现
所谓的简洁实现,就是使用Pytorch中提供的工具,来让实现更加的简单。
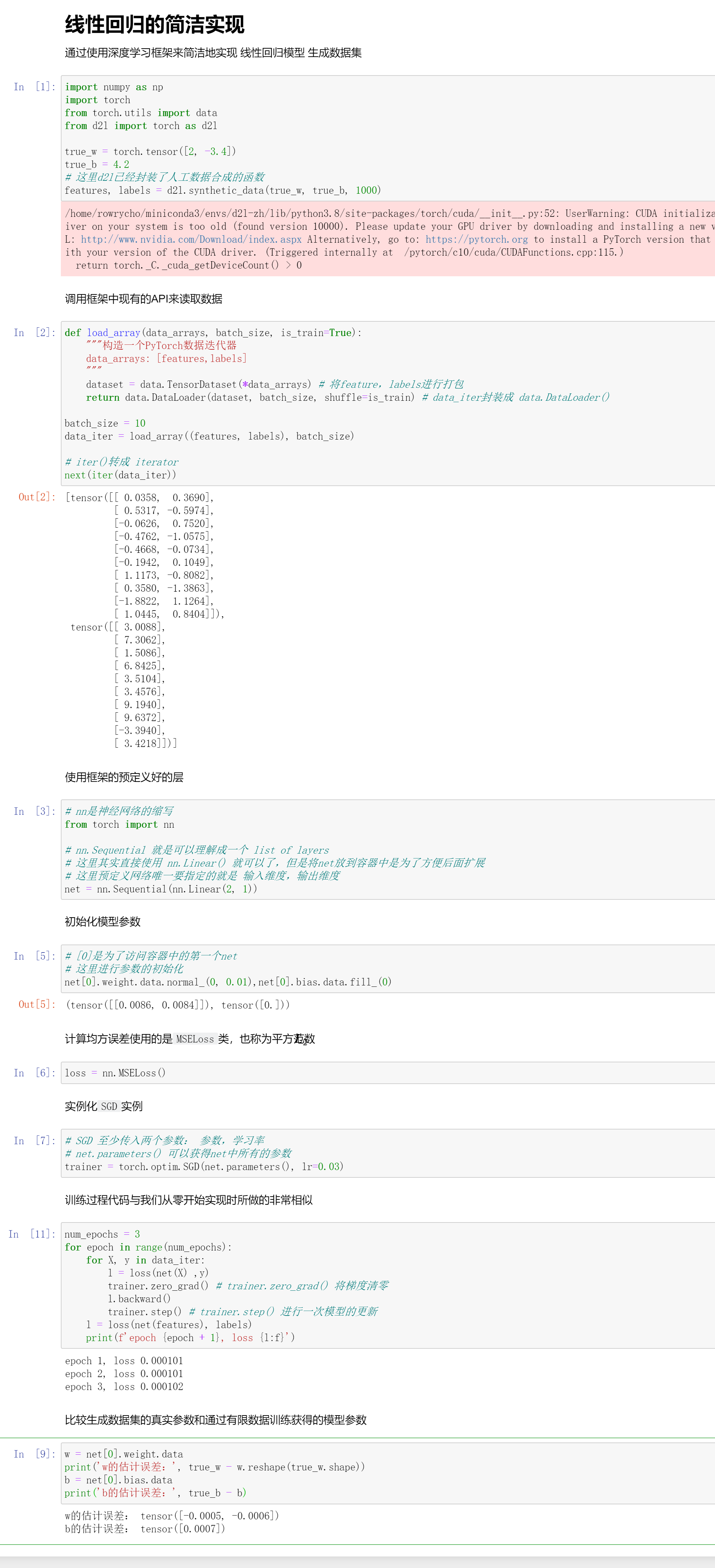
操作总结
import numpy as np
import torch from torch.utils
import data from d2l
import torch as d2l
true_w = torch.tensor([2, -3.4])
true_b = 4.2
feature,labels = d2l.syntheic_data(true_w,true_b,1000) # 人工构造数据
# 使用框架生成 data_iter
def load_array(data_arrays,batch_size,is_train=True):
dataset = data.TensorDataset(*data_arrays) # 封装数据集
return data.DataLoader(dataset,batch_size,shuffle=is_train) # 生成批数据
batch_size = 10
data_iter = load_array([features,labels],batch_size)
# 网络模型定义
from torch import nn
net = nn.Sequential(nn.Linear(2,1)) # w,b参数都封装在里面
# 初始化模型参数
net[0].weight.data.normal_(0, 0.01),net[0].bias.data.fill_(0)
# loss_fn
loss = nn.MSELoss()
# 实例化SGD
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
# 训练代码
num_epochs = 3
for epoch in range(num_epochs):
for X,y in data_iter:
l = loss(net(X),y)
trainer.zero_grad() # 将参数梯度清零
l.backward() # BP计算梯度
l.step() # 更新参数
l = loss(net(features),labels)
print(f'epoch {epoch + 1}, loss {l:f}')
QA
- 有没有什么比较好用的云平台?
google colab、kaggle上的notebook
- 为什么使用平方损失而不是绝对差值呢?
我们后面会讲平方损失和绝对值差值?其实二者的区别不大,最早大家用平方损失函数,是因为绝对差值是一个不可导的函数。
- 损失为什么求平均?
因为是batch_size个样本计算的损失,所以要除以batch_size。当然如果没有在对loss除batch_size,也可以对学习率除batch_size,其实都是一样的。
- 线性回归的loss是不是通常都是mse?
是的,通常都是这样子的
- 不管是gd还是sgd,怎么找到合适的学习率?
说实话,这个就是靠经验进行调整的。
- batch_size是否会最终影响模型结果?batch_size过小是否可能导致最终累计的梯度计算不准确?
其实batch_size小点是好的,大了反而不行。这个可能是比较反自觉的。
我们后面会讲到丢弃发dropout的时候,batch_size小,也就是在同样的计算下,也就是扫数据扫10遍,batch_size小,其实对收敛越好。为什么?SGD其实实际上是给模型带来了噪音,采样越小,实际上噪音越多,比如100w张图片,每次只采样2张图片,那么噪音是会很大的,和真实的方向就会差很远。
但是噪音对神经网络是件好事情,因为现在的深度神经网络都太复杂了,一定的噪音使得你不会走偏,(大家说你教小孩的时候不要一直夸他,糙一点,不见得对小孩是一件坏事情,可以更加鲁棒),可以使得模型更加鲁棒,对各种噪音的容忍度越来越好,整个模型的泛化性就会更好。
- 针对batchsize大小的数据集进行网络训练的时候,网络中每个参数更新世的减去的梯度是batchsize中每个样本对应参数梯度求和后取得平均值吗?
对的,因为梯度是线性的,所以一个一个梯度求,等价于一批梯度求和在取均值。因为梯度是一个线性关系,是可以这么进行操作的。
- 随机梯度下降中的“随机”是指的批量大小是随机的吗?
批量大小是固定的,随机指的是随机对样本进行抽样。
- 在深度学习上, 设置损失函数的时候,需要考虑正则吗?
需要的,但是正则项一般不放在损失函数中,我们把(l_2)损失函数和(loss)是分开的。
后面会讲到正则项,但其实没有太多用,我们还有其他很多很多的方法来做正则。
- detach()是什么作用?
可以理解成把变量从计算图中抽取出来,就不要计算梯度。
- 这样的data_iter写法,每次都把所有的输出load进去, 如果数据多的话,最后内存会爆掉吧?有什么办法吗?
是的,这样内存会爆掉。
如果数据有100个G的话,这样直接load进内存当然是不对的。但是这本教材中包括一般的数据集都不会有那么大,一般服务器的内存几十个G还是有的,10G、20G的数据直接load进去问题也不大 。
当然一般都是将数据放在硬盘上,然后在一点一点从硬盘中进行读取,如果担心效率问题,可以一次从硬盘中多读取几个批次的数据进入内存。
- 如果样本大小不是batch_size的整数倍,那需要随机剔除多余的样本吗?
这是一个细节的问题,假设样本数量为100,但是batch_size取的是60。
- 最常见的做法就是拿到一个小一点的样本,也就是大小为40。
- 还有就是可以直接丢弃最后这个40的样本
- 可以和下一个epoch要20个样本
- 优化算法里 /batch_size 但是最后一个batch里的样本个数没有这么多?
是的,这里是我们偷懒了,实际上还是需要进行一个特判。
真实有多少个,就应该除于多大的batch_size。
- 这里学习率不做衰减吗?有什么好的学习率衰减方法吗?
理论上,SGD要收敛,那么就是要不断的把学习率变小变小变小,但实际上有很多其他的方法,学习率不做衰减的话,其实也问题不大。
后面会讲一种方法,会根据梯度的大小来调整学习率,所以不做衰减其实问题也不大。
- 这里没有进行收敛的判断吗?直接认为设置epoch的大小吗?
-
最简单的判断收敛的方法就是看两个epoch之间的loss差别如果在1%的时候,那么就可以认为是收敛了。
-
或者可以有一个验证数据集,如果验证数据集的精度没有增加了,那么也可以认为是收敛了。
其实如果算力是支持的话,多跑几次epoch是没有关系的,就算是loss没有下降,可能在进行微调。理解为读书读了10遍,在读一遍其实也没有关系。
- 定义网路有一定要手动设置参数初始值吗?
其实是不用的,网络有自己的参数的默认值。
这里手动设置w和b的初始值是为了和之前的从零开始实现线性回归对应上。
后面就不会手动设置初始值了,也设置不过来(太多参数了)。
- 外层forloop中最后一行
l=loss(net(),labels)就是为了print吗?这里梯度要不要清零呢?
是的,就是为了print。
这里不用清零梯度,因为这里只是forward,而没有backward去更新参数。