BST,Splay平衡树学习笔记
1.二叉查找树BST
BST是一种二叉树形结构,其特点就在于:每一个非叶子结点的值都大于他的左子树中的任意一个值,并都小于他的右子树中的任意一个值。
2.BST的用处
如果利用朴素算法序列中的第k大的数,最坏的情况下可能达到O(N*logN),而由于BST的特性,我们可以把复杂度优化为O(logN),不仅如此,我们还可以在O(logn)的复杂度下查找元素,O(1)的复杂度下修改元素。对于有些数据来说,极大地节约了时间。
3.BST的优化---splay平衡树
再优秀的算法都会有自己的缺点,而BST的缺点就在于,在极端情况下,树形结构会退化为一条链,此时进行操作甚至比朴素算法还要劣。那啷个办嘞?肯定要想办法降低树的深度于是天空一声巨响,,神奇的splay,treap闪亮登场qwq。
每一次的询问值x,我们把他移到root的位置,在这样做的同时,我们维护好这个BST的性质(忘了的自己看第一条0_0)。就比如说,我们把这条链调成splay的形式:

是不是感觉优化过后好厉害~咳咳,下面还有更厉害的
优化核心:旋转操作Rotate
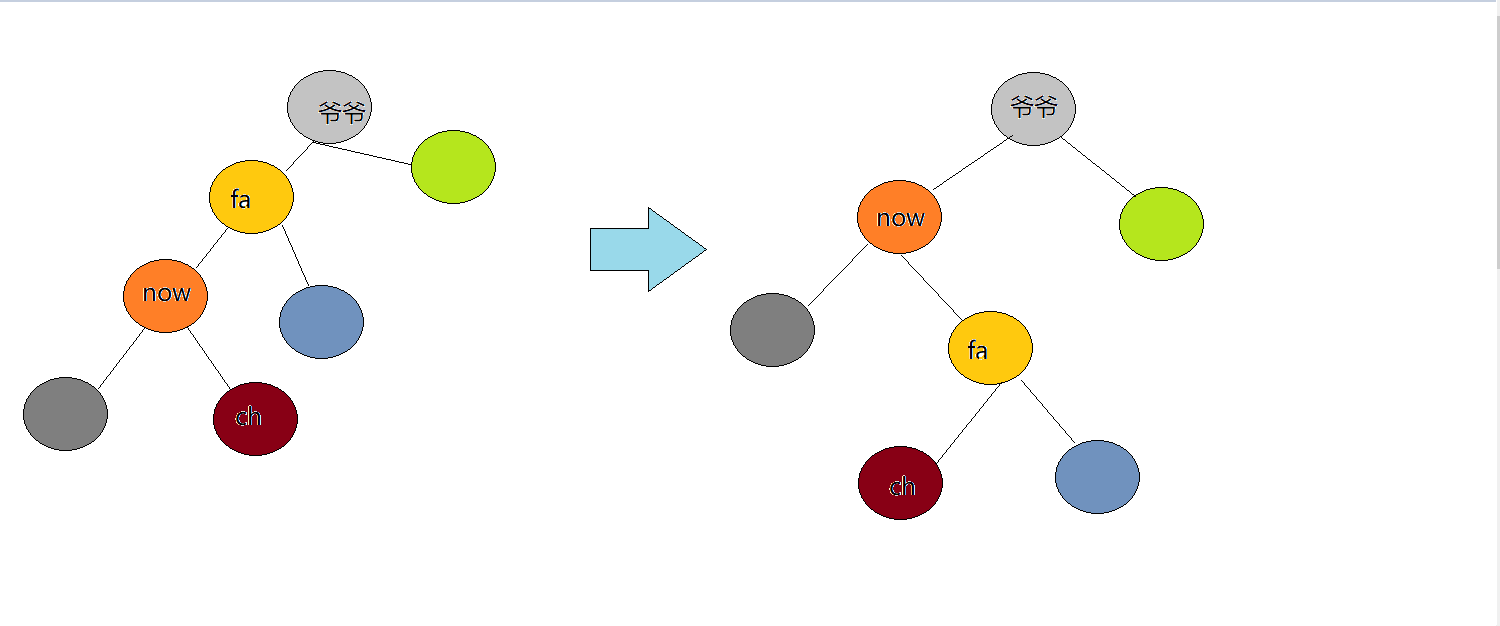
定义rotate(now,goal),将节点now旋转至goal节点处,同时,为了维护BST的性质,我们需要将树的结构进行调整:(这里只考虑把now转移到他的父亲fa)
step1:询问now,fa是他们父亲的哪个儿子假设查询结果为l_now,l_fa
step2:把now放到他父亲的位置上,维护节点信息之后我们来处理他原来的爸爸fa
step3:按道理来讲,fa由于比now大(其他情况自己画图我懒得动QAQ),fa本来应该变为now的右儿子(由于BST的性质),可是此时now已经有一个孩子ch了,如果强行接入,ch就没爸爸了,他会很伤心的,为了维护一棵快乐的BST,我们决定再给他找个爸爸,在上面操作中,fa失去了一个儿子(now变为了他的父亲),他现在也是难过的摇头晃脑,所以,我们不妨直接让fa领养ch,由于ch为原树中fa左子树中的结点,并且为now的右儿子,所以有如下关系:
now<ch<fa,刚好,将ch拿给fa当儿子完美的维护了BST的性质,所以,这是一个合法的操作(我们就可以给他发领养证啦:)),最后再维护一下结点信息就好啦QAQ
slpay操作就是不断地上旋直到达到目标,rotate则是单旋
下面上图:
//rotate操作我感觉讲的不是很清楚,这里推荐一下Clove学姐的文章,下面附上链接https://www.cnblogs.com/hua-dong/p/7822815.html
下面来道题练习一下:https://www.luogu.com.cn/problem/P3391
说实话这道题入门有点难,其实这里bst我维护的是输出的优先级,而翻转操作则是交换优先级,所以立刻想到交换中间结点的左右子树,那怎么保证以这个结点为根节点的子树完全且恰好包含题目要翻转的区间呢?
不妨这样考虑:对于每一个要翻转的区间,[l,r],我们把l-1号节点旋转到根节点处,再把r+1旋转到l-1的又孩子处,你们自己按照rotate转一下之后就会发现,我们要维护的区间恰好是根节点的右子树的左子树 'O' (手动惊讶Σ(⊙▽⊙"a)
就okk啦~
下面上代码,有注释滴,码风还好不用担心:
1 #include<iostream>
2 #include<cstdio>
3 #define N 100005
4
5 using namespace std;
6
7 int ch[N][2],fa[N],size[N],ans[N],val[N],n,m,root,cnt=0;
8 bool tag[N]={0};
9
10 int Read()
11 {
12 int num=0,k=1;
13 char c=getchar();
14 while(c!='-'&&((c>'9')||(c<'0'))) c=getchar();
15 if(c=='-')
16 {
17 k=-1;
18 c=getchar();
19 }
20 while(c>='0'&&c<='9')
21 {
22 num=(num<<3)+(num<<1)+c-'0',c=getchar();
23 }
24 return num*k;
25 }
26
27 void push_up(int x)
28 {
29 size[x]=size[ch[x][0]]+size[ch[x][1]]+1;
30 } //以x为root的子树中结点的个数
31
32 int locate(int x)
33 {
34 return ch[fa[x]][1]==x;
35 } // 定位x是他爸爸的哪个儿子
36
37 void rotate(int x) // 把x旋转到root
38 {
39 int y=fa[x],z=fa[y],b=locate(x),c=locate(y),a=ch[x][!b];
40 if(fa[y]) ch[z][c]=x ; //如果x的爸爸不是root
41 else
42 {
43 root=x;
44 fa[x]=z; //替代root的位置
45 }
46 if(a) fa[a]=y;ch[y][b]=a;//旋转
47 ch[x][!b]=y;
48 fa[y]=x;
49 push_up(y);
50 push_up(x);
51 }
52
53 int build(int l,int r,int f)//构造splay
54 {
55 int mid=(l+r)>>1;
56 val[mid]=ans[mid];
57 fa[mid]=f;
58 if(l<mid) ch[mid][0]=build(l,mid-1,mid);
59 if(mid<r) ch[mid][1]=build(mid+1,r,mid);
60 push_up(mid);
61 return mid;
62 }
63
64 void push_down(int x)
65 {
66 if(!tag[x]) return ;//x结点上覆盖了懒标记
67 tag[ch[x][0]]^=1;
68 tag[ch[x][1]]^=1;
69 swap(ch[x][0],ch[x][1]);
70 tag[x]=false;
71 }
72
73 int query(int x) //询问x在splay中的结点编号
74 {
75 int now=root;
76
77 while(true)
78 {
79 push_down(now);
80 if(ch[now][0]&&x<=size[ch[now][0]]) now=ch[now][0];//对于splay上值为a的结点有size[ch[now][0]]>=a这里判断是否在左子树
81 else
82 {
83 int num=(ch[now][0] ? size[ch[now][0]] :0) +1;//计算当前结点的编号:左子树根节点编号+1
84 if(num==x) return now;//
85 x-=num;
86 now=ch[now][1];
87 }
88 }
89 }
90
91 void splay(int x,int goal)//把now转为goal的子节点
92 {
93 while(fa[x]!=goal)
94 {
95 int y=fa[x],z=fa[y];
96 if(z==goal) rotate(x);//单旋
97 else
98 {
99 if(locate(x)==locate(y))
100 {
101 rotate(y);
102 rotate(x);
103 }
104 else
105 {
106 rotate(x);
107 rotate(x);
108 }
109 }
110 }
111 }
112
113 void print(int now)
114 {
115 push_down(now);
116 if(ch[now][0]) print(ch[now][0]);
117
118 ans[++cnt]=val[now];
119
120 if(ch[now][1]) print(ch[now][1]);
121
122 }
123
124 int main ()
125 {
126 int l,r;
127 n=Read(),m=Read();
128 for(int i=1;i<=n+2;i++) ans[i]=i-1;// 记录前驱
129
130 root=build(1,n+2,0);
131
132 for(int i=1;i<=m;i++)
133 {
134 l=Read(),r=Read();
135 int x=query(l),y=query(r+2); //查找x的前驱所在的位置,和y后驱所在的位置,因为预处理时ans存的是前趋,所以直接查找x,而y的后驱变成了y+2
136 splay(x,0);
137 splay(y,x); //将x前驱上旋至根节点,y的后驱上旋成根节点右儿子的左子树
138 tag[ch[ch[root][1]][0]]^=1;//经过旋转后,此时根节点的右儿子的左子树就是需要翻转的区间,所以lazy标记
139
140 }
141
142 print(root);
143
144 for(int i=1;i<=n;i++) printf("%d ",ans[i+1]);
145 return 0;
146 }
好啦,BST就到这里啦~第一次写文章,写的不好的地方原谅一下,也欢迎大家提问和指正,拜拜~
ps.转载记得注明出处哦,你看人家那么辛苦滴QAQ