NOI 2009 诗人小G

两天6 hours+我终于把这道题改完啦!!!!

呜呜呜呜决策单调性真的太鹅星了!!!

通过这道题对决策单调性有一定的认识了

先给自己补充几个知识点 来源是luogu题解的第一篇

四边形不等式

若对于定义域上的任意整数 a,b,c,d，其中a≤b≤c≤d，都有以下方程成立，则称函数w满足四边形不等式：

可将四边形不等式转化为另一种形式，其中 a<b ，请自行证明等价于上式：(代进去就好了)

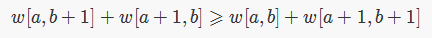
设 k[i]表示 f[i]的最优决策，若满足如下等式，则称f满足决策单调性：

要证明上述状态转移方程具有决策单调性，只需证明其满足四边形不等式：

证明：若满足四边形不等式，则 ∀i∈[1,n] , ∀j∈[0,k[i]−1] ，根据 k[i]k[i] 的最优性有：

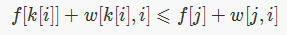
对于∀i′∈[i+1,n] ，因为 w 满足四边形不等式有：

移项得：

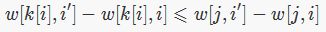
与第一个等式相加得：

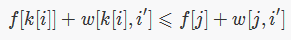
这个不等式的含义为，以 k[i] 作为 f[i'] 的决策，比以 j<k[i] 作为 f[i'] 的决策更优。

也就是说k[i′]≥k[i] ，所以 f 具有决策单调性。

 

决策单调性

下证状态转移方程 

 

具有决策单调性。

证明：四边形不等式如下：

 

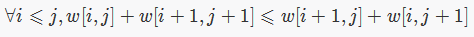
设 a[i]=S[i]+i,D[i]=l[i]+1,X=L+1，其中 a[i+1]=a[i]+D[i+1]。

则 w[j,i]=|a[i]-a[j]-X|^P  所以只需证明：

设 S=a[i]-a[j]-X, T=a[i+1]-a[i]-X ，则上式等价于：

 

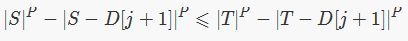
因为 T=S+D[i+1] ，且 D[i+1]>0 ，所以 S<T 。

故只需证明下列函数在整数域内 (非严格) 单调递增：

 

然后就是求导什么的 我不会...液！！等我以后学了求导来填这个坑...!!!

综上所述，状态转移方程 

 

具有决策单调性... 显然对我而言还是打表法和瞪眼法更有用..

 

 

好我补充的就差不多了 具体对这道题而言

有两个问题 1. dp值 2.输出方案

 

就是每一个点都有其对应的最优决策点

在每次更新之后要看下那些新的区间可以以我现在的点作为决策点

比较函数就是用方程来计算用b点更新a点的更新值 显然这个更新值越小越好

这时候就要对于原数组进行修改 但是对于原数组修改太慢了 就开一个结构体

储存对于以i作为最优决策点的区间的左端点和右端点 

然后开一个队列把这些区间都存进去 

每次在更新i点的时候就看一下i是否在目前的队首区间 不在就head ++

然后就更新 因为要输出方案 所以要记录一下他的决策点是什么

更新完了之后就处理出以i作为最优决策点的区间

怎么更新呢 他有可能覆盖掉之前的一整个区间

就像这样 011111111222   -> 011111333333 

以这个例子而言  就判断原来2区间的左端点和以3作为决策点哪个更优

若3更优 就把2弹出队列 tail - -  然后在最后这个区间里面二分找出最优决策点就可以了

为什么队列不会弹空呢 因为如果要弹空的话 那么一号点早就已经更新过了 

这个时候在妄图覆盖掉不会在用的点是不明智的 也是不合法的..（总不可能用后面的点去搞前面吧）

（当然我觉得在每次弹的时候判断一下队尾区间的右端点是否小于i 如果小于就不弹了也是ok的）

但是也有可能这个新的i作为决策点一点用都没有

那么就在弹之前判断一下用 i 和原来队尾哪个更新n更优 如果 i 更劣 那么就直接continue就好了

但是有一个至今都在困扰我的问题 就是在二分的时候为什么判断条件一定要是≤ 而不是<

这个有什么影响吗???用他们去更新对应点答案不是一样的吗 除了区间会变以外 

但是在二分的时候他也会搞到这个东西啊 为什么dp值会出问题呢????

（但是这个会影响方案的输出 但是我认为如果一样 输出的都是合法方案）

 

第二个问题就是输出方案 因为我们记录了每个点从哪个点转移而来的

所以就从n来倒着搞  搞出每个点可以转移到哪个点

转移点是作为它那一行的最后一句话的 他的转移过去的点也是作为那行的最后一句话

就依次输出对应的一行就好了

差不多就是这个样子吧

代码

#include <bits/stdc++.h>
#define oo 1e18
typedef long double ld;

using namespace std;

const int N = 1e5 + 5;

int T,from[N],que[N],L,P,n,sum[N],nxt[N];
ld f[N];
char s[N][35];

struct section {
    
    int l,r;
}sec[N];

void init( ) {
    
    memset(s,0,sizeof(s));
    memset(f,0,sizeof(f));
    memset(nxt,0,sizeof(nxt));
    memset(from,0,sizeof(from));
    memset(que,0,sizeof(que));
    memset(sec,0,sizeof(sec));
    for(int i = 1;i <= n;i ++) {
        scanf("%s",s[i] + 1);
        int len = strlen(s[i] + 1);
        sum[i] = sum[i - 1] + len + 1;
    }
}

ld fast_pow(ld a,int b) {
    
    ld ans = 1;
    for(;b;b >>= 1,a = a * a)
      if(b & 1) ans = ans * a;
    return ans;
}

ld cmp(int a,int b) {
    
    ld ans = f[a] + fast_pow(abs(sum[b] - sum[a] - L - 1),P);
    return ans;
}

void solve( ) {
    
    int h = 1,t = 0;
    que[++ t] = 0;
    sec[t].l = 1; sec[t].r = n;
    for(int i = 1;i <= n;i ++) {
        
        while(h < t && sec[que[h]].r < i) h ++;
        f[i] = f[que[h]] + fast_pow(abs(sum[i] - sum[que[h]] - 1 - L),P);
        from[i] = que[h];
        if (cmp(que[t],n) < cmp(i, n)) continue;
        while(h < t && cmp(i,sec[que[t]].l) < cmp(que[t],sec[que[t]].l)) {
            sec[que[t]].l = 0;
            sec[que[t]].r = 0;
            t --;
        }
        int lf = sec[que[t]].l,rg = n;
        int ans = rg + 1;
        while(lf <= rg) {
            int mid = (lf + rg) >> 1;
            ld aa = cmp(i,mid); 
            ld bb = cmp(que[t],mid);
            if(aa <= bb) {
                rg = mid - 1;
                ans = mid;
            }
            else lf = mid + 1;
        }
        sec[que[t]].r = ans - 1; que[++ t] = i;
        sec[que[t]].l = ans; sec[que[t]].r = n;
     }
}

void print( ) {
    
    if(f[n] > oo) {
        printf("Too hard to arrange
");
    }
    else {
        printf("%lld
",(long long)(f[n] + 0.5));
        for (int i = n;i;i = from[i]) {
                nxt[from[i]] = i;
            }
            for (int i = 1,cur = 0;i <= n;i = cur + 1) {
                cur = nxt[cur];
                for (int j = i;j < cur;j++) {
                    printf("%s ", s[j] + 1);
                }
                printf("%s
",s[cur] + 1);
            }
    }
    printf("--------------------
");
}

int main( ) {
    
    scanf("%d",& T);
    while(T --) {
        
        scanf("%d%d%d",& n,& L,& P);
        init( );
        solve( );
        print( );
    }
}