题目描述
在河上有一座独木桥,一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子,青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数,我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点:0,1,…,L(其中L是桥的长度)。坐标为0的点表示桥的起点,坐标为L的点表示桥的终点。青蛙从桥的起点开始,不停的向终点方向跳跃。一次跳跃的距离是S到T之间的任意正整数(包括S,T)。当青蛙跳到或跳过坐标为L的点时,就算青蛙已经跳出了独木桥。
题目给出独木桥的长度L,青蛙跳跃的距离范围S,T,桥上石子的位置。你的任务是确定青蛙要想过河,最少需要踩到的石子数。
输入输出格式
输入格式:
第一行有1个正整数L(1≤L≤109),表示独木桥的长度。
第二行有3个正整数S,T,M,分别表示青蛙一次跳跃的最小距离,最大距离及桥上石子的个数,其中1≤S≤T≤10,1≤M≤100。
第三行有M个不同的正整数分别表示这MM个石子在数轴上的位置(数据保证桥的起点和终点处没有石子)。所有相邻的整数之间用一个空格隔开。
输出格式:
一个整数,表示青蛙过河最少需要踩到的石子数。
输入输出样例
说明
对于30%的数据,L≤10000;
对于全部的数据,L≤10^9。
首先看到这道题目很容易想到跑dp的哇 然而定睛一看这个数据范围..... 1e9...
再见再见 是在下输了...
但是想来想去还是只有垃圾dp 然后又看到石头的数量是特别少的 所以很容易出现两个石头之间的路径特别特别长
所以就考虑压缩路径
想想怎么压缩呢 又可以看到每一步跳的范围也是很小的 在 $10$ 以内 所以考虑用 $lcm$ 压缩路径 并且使这段路径可以正常跑dp
怎么用 $lcm$ 压缩呢 如图 对于两块石头 $a,b$ 的一段路径 假定我们的压缩路径每段长度为 $2520$ ($1$ 到 $10$ 的$lcm$)
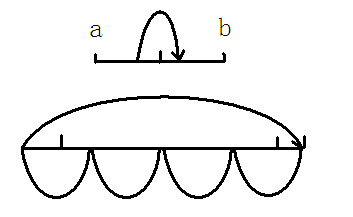
上面是压缩之后的 假设这一步距离为 $x$ 那么有他按照这个步伐不变 跳出压缩路径之后仍然落在这个点上
设跳完这段路径要$k$ 步 则需要判断$2520 + x$ 与 $k * x$ 的关系
因为 $2520$ 是 $x$ 的倍数 所以 $x | 2520 + x$ 也就是说他会跳在同一个点 压缩路径成功
所以具体实现就是两块石头之间的路径长度模 $2520$ 剩下的长度正常跑 $dp$ 就可以了
代码
#include <bits/stdc++.h> using namespace std; const int N = 3 * 1e6 + 5; const int mod = 2520; int n,L,S,T; int dp[N],st[300],f[300]; bool vis[N]; int dis[105][105]; int main( ) { scanf("%d",& L); scanf("%d%d%d",& S,& T,& n); for(int i = 1;i <= n;i ++) { scanf("%d",& st[i]); } st[n + 1] = L; sort(st + 1,st + n + 2); int las = 0; f[0] = 0; memset(dp,0x3f3f3f,sizeof(dp)); dp[0] = 0; for(int i = 1;i <= n + 1;i ++) { f[i] = f[i - 1] + (st[i] - st[i - 1]) % mod; if(i != n + 1) vis[f[i]] = true; } for(int i = 1;i <= f[n + 1] + T;i ++) { for(int j = S;j <= T;j ++) { if(i - j < 0) break; if(vis[i]) dp[i] = min(dp[i],dp[i - j] + 1); else dp[i] = min(dp[i],dp[i - j]); } } int ans = 10000000; for(int i = f[n + 1];i <= f[n + 1] + T;i ++) ans = min(ans,dp[i]); printf("%d",ans); }