tyvj 1198 矩阵连乘
题目描述
一个n*m矩阵由n行m列共n*m个数排列而成。两个矩阵A和B可以相乘当且仅当A的列数等于B的行数。一个N*M的矩阵乘以一个M*P的矩阵等于一个N*P的矩阵,运算量为n*m*p。 矩阵乘法满足结合律,A*B*C可以表示成(A*B)*C或者是A*(B*C),两者的运算量却不同。例如当A=2*3 B=3*4 C=4*5时,(A*B)\*C=64而A\*(B*C)=90。显然第一种顺序节省运算量。 现在给出N个矩阵,并输入N+1个数,第i个矩阵是a[i-1]*a[i]。
输入格式
第一行n(n<=100);
第二行n+1个数;
输出格式
最优的运算量
样例
样例输入
3
2 3 4 5
样例输出
64
解释:
可能大部分同学连题目都没有看懂,其实是很好理解的。
如题目中的A、B、C,A*B=2*3*4,B*C=3*4*5。
可以这么理解:两个矩阵(长宽中必须有一个相同)相乘,讲相同部分放中间,剩下两个不同的部分在两边相乘。如:A:x*y
B:y*z
C:z*l
A*B=x*y*z; B*C=y*z*l;
那么三个矩阵相乘是什么样的呢?
还是按上面的例子:(A*B)*C=(x*y*z)*C,显然A*B后的矩阵长宽都发生了变化,变化的是:y的边去掉,x与z取相乘,则乘了后,矩阵变为了x*z
如图:
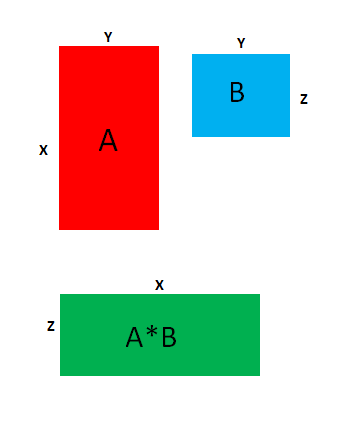
所以,则(A*B)*C=(x*y*z)+(x*z*l),A*(B*C)=(x*y*l)+(y*z*l)
注意:
题中求的是运算量,与矩阵相乘后的结果不一样,相乘后的结果只是用来求下一次相乘的运算量。
样例模拟:
a[i]与a[i+1]即第i个矩阵
A:2*3;B:3*4;C:4*5
(A*B)*C:2*3*4+2*4*5=64;
A*(B*C):2*3*5+3*4*5=90;
故最小的运算量=64
动态转移方程:
f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+a[i-1]*a[j]*a[k]);
f[i][j]:从i到j的最小的运算量
f[i][j]之间分开,分成i到k与k+1到j两个区间,现在就可以看出是很简单区间dp,在将运算量加上,取最小值
代码:
#include<bits/stdc++.h> using namespace std; const int maxe=1e2+5,maxn=1e2+5,INF=0x3f3f3f3f; int n,m,f[maxe][maxe],sum[maxn],a[maxn]; int main(){ cin>>n; memset(f,0x3f,sizeof(f));//初始成最大去最小值 for(int i=0;i<=n;i++)cin>>a[i]; for(int i=1;i<=n+1;i++)f[i][i]=0;//相同之间的运算量为0 for(int d=2;d<=n;d++){//枚举长度 for(int i=1,j;(j=i+d-1)<=n;i++){ for(int k=i;k<j;k++){ f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+a[i-1]*a[j]*a[k]); } } } cout<<f[1][n]<<endl;//输出1到n的最小运算量
return 0; }