步步为零——巧妙的dp

步步为零

题目描述

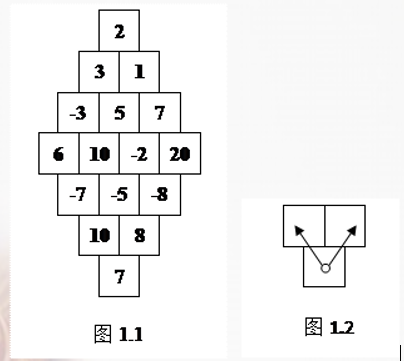
你是否听说过这个游戏？游戏者在一张特殊的表格中按照规则跳动，使得跳到的数字经过加号和减号的连接，尽可能的逼近零。表格通常是如图 (1.1) 所示的形状，大小由中间一行的方格数 (N) 决定(图 (1.1) 就是一个 (N=4) 的例子)。

游戏者通常是从最下面的方格出发，按照如图 (1.2) 所示的规则在表格中跳动，当游戏者跳到最顶端的方格时，游戏结束。在游戏未结束前，游戏者不允许跳到表格外。

将游戏者跳到的 (2 imes N-1) 个数字依次写下来，在每两个相邻的数字中间加上加号或减号，使得计算结果最接近零。

例如对于图 (1.1) 所示的表格，最好的跳动及计算方案是：
(7+8+(-5)+(-2)-5-1-2=0)
或(7+10+(-7)-6+(-3)-3+2=0)
或(7+10+(-5)-10-5+1+2=0)
或(7+10+(-5)+(-2)-5-3-2=0) 。

输入格式

输入文件的第一行是 (N(Nleq 50))，接下来(2 imes N-1)行给出了表格中每行的每个方格中的数字，第 (i+1) 行的第 (j) 个数字对应于表格中第 (i) 行的第 (j) 个数字。

文件中第二行的数字表示的是表格顶端的方格中的数字。文件中所有的数字都是整数，同一行相邻的两个数字间用空格符隔开

输出格式

输出文件只有一行，是你所求出的最接近零的计算结果的绝对值。

样例

样例输入

4
2
3 1
-3 5 7
6 10 -2 20
-7 -5 -8
10 8
7

样例输出

0

数据范围与提示

表格中的所有数字大于等于 (-50)，小于等于 (50) 。

思路

如果我们像样例输入中一样将每个数字存在数组里，会发现，在第 (n) 行以上的数能移动到上面和左上的位置，在第 (n) 行以下的数能移动到上面和右上的位置。

当我们输入的时候，我们可以只存储它的绝对值，毕竟既可以加又可以减，存负数的绝对值并不影响。

定义一个 (dp[i][j][now]) ，表示在第 (i) 行，第 (j) 列，(now) 值能否取到。

但是我们发现 (now) 值可能是正值也可能是负值，但是负数的下标是不被允许的。

所以我们在存储的时候可以把能取到的最大值 (tot) 求出来，将 (now) 加上 (tot)，便可以保证 (now) 值不会是负数，我们就从 (-tot—tot)，转移成了 (0—2 imes tot)。

暴力代码

#include<bits/stdc++.h>
using namespace std;

const int maxn=100+50,INF=0x3f3f3f3f;
int n;
int ans=INF;
int pan[maxn][maxn];

void Dfs(int x,int y,int cnt){
	if(x==1&&y==1){//到达顶端
		int ans1=abs(cnt+pan[x][y]);
		int ans2=abs(cnt-pan[x][y]);
		int ans3=min(ans1,ans2);
		ans=min(ans,abs(ans3));
		return;
	}
	if(x>n){//在下半部分
		Dfs(x-1,y,cnt+pan[x][y]);//向上走
		Dfs(x-1,y,cnt-pan[x][y]);
		Dfs(x-1,y+1,cnt+pan[x][y]);//向右上走
		Dfs(x-1,y+1,cnt-pan[x][y]);
	}else if(x<=n){//在上半部分
		if(y==1){//考虑边界，在最左边
			Dfs(x-1,y,cnt+pan[x][y]);//只能向上走
			Dfs(x-1,y,cnt-pan[x][y]);
		}else if(x==y){//在最右边
			Dfs(x-1,y-1,cnt+pan[x][y]);//只能向左上走
			Dfs(x-1,y-1,cnt-pan[x][y]);
		}else{
			Dfs(x-1,y-1,cnt+pan[x][y]);//向左上走
			Dfs(x-1,y-1,cnt-pan[x][y]);
			Dfs(x-1,y,cnt+pan[x][y]);//向上走
			Dfs(x-1,y,cnt-pan[x][y]);
		}
	}
}
int main(){
	scanf("%d",&n);
	int pd=1;
	int m=1;
	for(int i=1;i<=2*n-1;i++){
		for(int j=1;j<=m;j++){
			scanf("%d",&pan[i][j]);
		}
		if(pd==1)m++;
		else if(pd==0)m--;
		if(m==n){
			pd=0;
		}
	}
	Dfs(2*n-1,1,0);
	cout<<ans<<endl;
	return 0;
}

暴力并不需要进行转换，只是普通的 (Dfs) 即可，但是时间效率很差，只能过几个点。

正解代码

#include <bits/stdc++.h>
using namespace std;

const int maxn=100+50,INF=0x3f3f3f3f;
int n;
int pan[maxn][maxn];
int tot;
int Max;
int ans=INF;
int dp[maxn][maxn][5050];//这里需要计算一下最大值来确定第三维的大小
bool Pd(int x){//没用的判断，肯定走不出去
	if(x<0||x>2*tot)return false;
	else return true;
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			scanf("%d",&pan[i][j]);
			pan[i][j]=abs(pan[i][j]);
			Max=max(Max,pan[i][j]);
		}
		tot+=Max;
		Max=0;
	}
	Max=0;
	for(int i=n+1;i<=2*n-1;i++){
		for(int j=1;j<=2*n-i;j++){
			scanf("%d",&pan[i][j]);
			pan[i][j]=abs(pan[i][j]);
			Max=max(Max,pan[i][j]);
		}
		tot+=Max;
		Max=0;
	}
	dp[2*n-1][1][tot]=1;//初始在最下面能取到
	int now=0;
	for(int i=2*n-1;i>=n+1;i--){//dp下半部分
		for(int j=1;j<=2*n-i;j++){
			for(int k=0;k<=2*tot;k++){
				if(dp[i][j][k]){//k能取到，往上进行
					now=k+pan[i][j];
					if(Pd(now)){//没用的判断
						dp[i-1][j][now]=1;
						dp[i-1][j+1][now]=1;
					}
					now=k-pan[i][j];
					if(Pd(now)){//没用的判断
						dp[i-1][j][now]=1;
						dp[i-1][j+1][now]=1;
					}
				}
			}
		}
	}
	for(int i=n;i>=1;i--){//dp上半部分
		for(int j=1;j<=i;j++){
			for(int k=0;k<=2*tot;k++){
			      	if(dp[i][j][k]){//k能取到，往上进行
					now=k+pan[i][j];
					if(Pd(now)){//没用的判断
						dp[i-1][j][now]=1;
						dp[i-1][j-1][now]=1;
					}
					now=k-pan[i][j];
					if(Pd(now)){//没用的判断
						dp[i-1][j][now]=1;
						dp[i-1][j-1][now]=1;
					}
				}
			}
		}
	}
	for(int i=0;i<=2*tot;i++){
		if(dp[0][0][i]){
			ans=min(ans,abs(i-tot));//别忘了减掉tot
		}
		if(dp[0][1][i]){//其实这两个值相同，取一个即可
			ans=min(ans,abs(i-tot));
		}
	}
       	printf("%d
",ans);
	return 0;
}