一个人做到只剩了回忆的时候,生涯大概总要算是无聊了吧,但有时竟会连回忆也没有。 ——鲁迅 《朝花夕拾》
(PS):由于这部分在疫情里(Hugecolor{blue} 氵)掉了,或是好久之前学过但现在忘却的,时而回忆,以记于心。
差分约束
概念&定义
如果一个系统由 (n) 个变量和 (m) 个约束条件组成,形成 (m)个 形如 (a_i-a_jleq k) 的不等式((i,jin [1,n],k) 为常数),则称其为差分约束系统((system; of; difference; constraints)) 。
引例
给出 (n) 个变量,(m) 个形如 (x_i- x_jleq w(i,jin [0,n - 1])) 不等式,求出 (x_{n-1}-x_0) 的最大值。
如下 (3) 个不等式:
经运算,得出:
可以发现,我们用 (1,2) 式推出 (x_2) 与 (x_0) 的关系的过程,与 (SPFA) 中的松弛操作类似,考虑和图论建立关系。
我们可以将形如 (x_i- x_jleq w(i,jin [0,n - 1])) 不等式,转移到图上,建一条 (x_j) 到 (x_i) 的边权为 (w) 的有向边。
按照这个套路,我们可以将上面的不等式组建成下面的一个图:
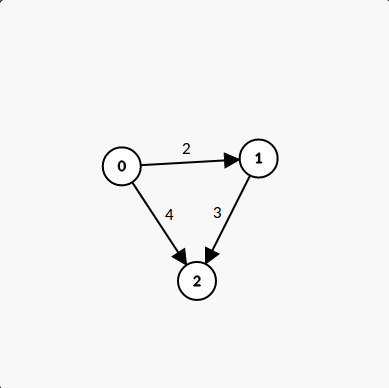
问题转成了:求 (x_0) 到 (x_{n-1}) 的最短路,(SPFA) 即可。
解的存在性
(SPFA) 会出现负环和终点不可达的特殊情况,差分约束系统中同样存在:
负环
比如这 (3) 个不等式:
在图中是如下情况:

会发现:(dis_{n-1}-dis_0leq w) 中的 (w) 在无限减小,会使 (dis) 值不断减小,造成了无解的情况。
在 (SPFA) 中体现为 (1) 个点入队次数超过总点数 (n) 。
终点不可达
显然是 (x_{n-1}) 与 (x_0) 不存在直接/间接的约束关系,也不会有解。
在 (SPFA) 中体现为 (dis_{n-1} = INF) 。
灵活性
当问题的不等关系不是 (leq) 的情况时,可以根据一些基础的数学知识将符号转化成解题所需的不等号,如:
-
(a - b < c) 转化为 (a-bleq c - 1)
-
(a - b geq c) 转化为 (b - a leq - c)
-
(a - b = c) 转化为 (a - b leq c) 和 (b - a leq - c)
-
(a = b) 转化为 (a - b leq 0) 和 (b - a leq 0)
这使我们的差分约束更加灵活,在不同的题意下更加灵活多变。
结论
当我们求形如求 (x_{n-1} - x_0) 的最大值的问题,可以将不等式转化为 (leq) 的性质,求最短路。
当我们求形如求 (x_{n-1} - x_0) 的最小值的问题,可以将不等式转化为 (geq) 的性质,求最长路。
例题
某谷板子
思路
板子,直接看代码就行了。
代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int maxn = 1e5 + 50, INF = 0x3f3f3f3f;
inline int read () {
register int x = 0, w = 1;
register char ch = getchar ();
for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
return x * w;
}
inline void write (register int x) {
if (x / 10) write (x / 10);
putchar (x % 10 + '0');
}
int n, m;
struct Edge {
int to, next, w;
} e[maxn << 1];
int tot, head[maxn];
inline void Add (register int u, register int v, register int w) {
e[++ tot].to = v;
e[tot].w = w;
e[tot].next = head[u];
head[u] = tot;
}
int dis[maxn], cnt[maxn];
bool vis[maxn];
inline void SPFA (register int x) {
memset (dis, 0x3f, sizeof dis);
memset (vis, 0, sizeof vis);
queue <int> q;
q.push (x), dis[x] = 0;
while (! q.empty ()) {
register int u = q.front ();
q.pop (), vis[u] = 0;
for (register int i = head[u]; i; i = e[i].next) {
register int v = e[i].to;
if (dis[v] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
if (! vis[v]) {
vis[v] = 1, q.push (v);
if (++ cnt[v] > n) puts ("NO"), exit (0); // 判断无解
}
}
}
}
}
int main () {
n = read(), m = read();
for (register int i = 1; i <= m; i ++) {
register int u = read(), v = read(), w = read();
Add (v, u, w); // 注意是减号后的变量向前建边
}
for (register int i = 1; i <= n; i ++) { // 大多数差分约束都用到的操作
Add (0, i, 0); // 建一个0的虚点,向每一个点建边,且边权为0,不会对答案造成影响
}
SPFA (0);
for (register int i = 1; i <= n; i ++) printf ("%d ", dis[i]);
putchar ('
');
return 0;
}
小 K 的农场
思路
用一下数学知识转换一下柿子即可。
小声bb:最近题解越来越skyh了
代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int maxn = 1e5 + 50, INF = 0x3f3f3f3f;
inline int read () {
register int x = 0, w = 1;
register char ch = getchar ();
for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
return x * w;
}
inline void write (register int x) {
if (x / 10) write (x / 10);
putchar (x % 10 + '0');
}
int n, m;
struct Edge {
int to, next, w;
} e[maxn << 1];
int tot, head[maxn];
inline void Add (register int u, register int v, register int w) {
e[++ tot].to = v;
e[tot].w = w;
e[tot].next = head[u];
head[u] = tot;
}
int dis[maxn], cnt[maxn];
bool vis[maxn];
inline void SPFA (register int x) {
memset (dis, 0x3f, sizeof dis);
memset (vis, 0, sizeof vis);
queue <int> q;
q.push (x), dis[x] = 0;
while (! q.empty ()) {
register int u = q.front ();
q.pop (), vis[u] = 0;
for (register int i = head[u]; i; i = e[i].next) {
register int v = e[i].to;
if (dis[v] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
if (! vis[v]) {
vis[v] = 1, cnt[v] ++;
if (cnt[v] > n) puts ("No"), exit (0);
q.push (v);
}
}
}
}
}
int main () {
n = read(), m = read();
for (register int i = 1; i <= m; i ++) {
register int opt = read(), u = read(), v = read();
if (opt == 1) {
register int w = read();
Add (u, v, -w);
} else if (opt == 2) {
register int w = read();
Add (v, u, w);
} else {
Add (u, v, 0), Add (v, u, 0);
}
}
for (register int i = 1; i <= n; i ++) Add (0, i, 0);
SPFA (0), puts ("Yes");
return 0;
}
[HNOI2005]狡猾的商人
思路
其实式子是一个前缀和 (sum[r] - sum[l - 1] = w) 。
转化为 (sum[r] - sum[l - 1] leq w) 和 (sum[l - 1] - sum[r] leq - w),跑遍 (SPFA) 即可。
代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int maxn = 1e5 + 50, INF = 0x3f3f3f3f;
inline int read () {<details>
<summary>代码</summary>
register int x = 0, w = 1;
register char ch = getchar ();
for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
return x * w;
}
inline void write (register int x) {
if (x / 10) write (x / 10);
putchar (x % 10 + '0');
}
int T, n, m;
struct Edge {
int to, next, w;
} e[maxn << 1];
int tot, head[maxn];
inline void Add (register int u, register int v, register int w) {
e[++ tot].to = v;
e[tot].w = w;
e[tot].next = head[u];
head[u] = tot;
}
int dis[maxn], cnt[maxn];
bool vis[maxn];
inline void Init () {
tot = 0;
memset (e, 0, sizeof e);
memset (cnt, 0, sizeof cnt);
memset (head, 0, sizeof head);
}
inline bool SPFA (register int x) {
memset (dis, 0x3f, sizeof dis);
memset (vis, 0, sizeof vis);
queue <int> q;
q.push (x), dis[x] = 0;
while (! q.empty ()) {
register int u = q.front ();
vis[u] = 0, q.pop ();
for (register int i = head[u]; i; i = e[i].next) {
register int v = e[i].to;
if (dis[v] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
if (! vis[v]) {
vis[v] = 1, q.push (v);
if (++ cnt[v] > n) return 0;
}
}
}
}
return 1;
}
int main () {
T = read();
while (T --) {
n = read(), m = read(), Init ();
for (register int i = 1; i <= m; i ++) {
register int u = read(), v = read(), w = read();
Add (u - 1, v, w), Add (v, u - 1, - w); // 转化后的式子
}
if (SPFA (0)) puts ("true");
else puts ("false");
}
return 0;
}
[USACO05DEC]Layout G
思路
差分约束完美板子题,不知道为啥是紫。
处理好上面讲的两种特殊情况,先建虚点,跑一边 (SPFA (0)),判断一下解的存在,再跑 (SPFA(1))(最优情况下,编号为 (1) 的牛放到 (0) 显然会更优),输出 (dis[n]) 即可。
代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int maxn = 1e5 + 50, INF = 0x3f3f3f3f;
inline int read () {
register int x = 0, w = 1;
register char ch = getchar ();
for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
return x * w;
}
inline void write (register int x) {
if (x / 10) write (x / 10);
putchar (x % 10 + '0');
}
int n, m, k;
struct Edge {
int to, next, w;
} e[maxn << 1];
int tot, head[maxn];
inline void Add (register int u, register int v, register int w) {
e[++ tot].to = v;
e[tot].w = w;
e[tot].next = head[u];
head[u] = tot;
}
int dis[maxn], cnt[maxn];
bool vis[maxn];
inline void SPFA (register int x) {
memset (dis, 0x3f, sizeof dis);
memset (vis, 0, sizeof vis);
queue <int> q;
q.push (x), dis[x] = 0;
while (! q.empty ()) {
register int u = q.front ();
q.pop (), vis[u] = 0;
for (register int i = head[u]; i; i = e[i].next) {
register int v = e[i].to;
if (dis[v] > dis[u] + e[i].w) {
dis[v] = dis[u] + e[i].w;
if (! vis[v]) {
vis[v] = 1, q.push (v);
if (++ cnt[v] > n) puts ("-1"), exit (0);
}
}
}
}
if (x == 1) {
if (dis[n] == INF) puts ("-2"), exit (0);
printf ("%d
", dis[n]);
}
}
int main () {
n = read(), m = read(), k = read();
for (register int i = 1; i <= m; i ++) {
register int u = read(), v = read(), w = read();
Add (u, v, w);
}
for (register int i = 1; i <= k; i ++) {
register int u = read(), v = read(), w = read();
Add (v, u, -w);
}
for (register int i = 1; i <= n; i ++) Add (0, i, 0);
SPFA (0), SPFA (1);
return 0;
}
[POI2012]FES-Festival
思路
波兰人就是不一样,差分约束用 (Floyd) 写,既然做人家的题,就按照人家的思路来呗。
首先分析一下我们要求的是什么?
我们将条件转化成 (x_i-x_j leq w) 的形式,最后我们建出来的图的最长路加 (1) 就是我们要求的答案。
为什么?
转化一下式子:(x_ileq x_j + w),(x_i) 的取值是 ([x_j,x_j+w]) 这个范围内的,取值个数是 (w + 1),我们跑最长路求出来的是最大的 (sum w),加上 (1),就是我们的答案。
会发现,建完图,这是一个由多个联通块组成的图,对每一个联通块跑最长路,答案就是他们的和。
很好解释:
若有两个联通块,(1,2) 在一个联通块里,(3,4) 在一个联通块里,(1,2) 会互相限制,(3,4) 会互相限制,但是两个联通块之间没有约束关系,所以一个联通块取 (2) 个值,加起来就是 (4) 个,所以,我们求的就是这个和。
(Tarjan) 缩完点后,在每个联通块求最长路,它们加 (1) 的和,就是我们所求的答案。
代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
typedef long long ll;
using namespace std;
const int maxn = 6e2 + 50, maxm = 1e5 + 50, INF = 0x3f3f3f3f;
inline int read () {
register int x = 0, w = 1;
register char ch = getchar ();
for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
return x * w;
}
inline void write (register int x) {
if (x / 10) write (x / 10);
putchar (x % 10 + '0');
}
int n, m1, m2, ans;
int f[maxn][maxn];
struct Edge {
int to, next, w;
} e[maxm << 1];
int tot, head[maxn];
inline void Add (register int u, register int v, register int w) {
e[++ tot].to = v;
e[tot].w = w;
e[tot].next = head[u];
head[u] = tot;
}
bool vis[maxn];
int dfn[maxn], low[maxn], belong[maxn], st[maxn];
int sum, top, tic;
inline void Tarjan (register int u) {
dfn[u] = low[u] = ++ tic;
st[++ top] = u, vis[u] = 1;
for (register int i = head[u]; i; i = e[i].next) {
register int v = e[i].to;
if (! dfn[v]) {
Tarjan (v);
low[u] = min (low[u], low[v]);
} else if (vis[v]) {
low[u] = min (low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
sum ++;
while (st[top + 1] != u) {
register int v = st[top --];
belong[v] = sum, vis[v] = 0;
}
}
}
int main () {
n = read(), m1 = read(), m2 = read(), memset (f, 0x3f, sizeof f);
for (register int i = 1; i <= n; i ++) f[i][i] = 0; //Floyd初始化
for (register int i = 1; i <= m1; i ++) {
register int u = read(), v = read();
Add (u, v, 1), Add (v, u, -1), f[u][v] = min (f[u][v], 1), f[v][u] = min (f[v][u], -1); //要求的是最短路,所以重边的边权取min
}
for (register int i = 1; i <= m2; i ++) {
register int u = read(), v = read();
Add (v, u, 0), f[v][u] = min (f[v][u], 0);
}
for (register int i = 1; i <= n; i ++) Add (0, i, 0);
for (register int i = 1; i <= n; i ++) if (! dfn[i]) Tarjan (i);
for (register int k = 1; k <= n; k ++) {
for (register int i = 1; i <= n; i ++) {
for (register int j = 1; j <= n; j ++) {
f[i][j] = min (f[i][j], f[i][k] + f[k][j]);
}
}
}
for (register int i = 1; i <= n; i ++) if (f[i][i] < 0) return puts ("NIE"), 0; //Floyd判负环,即到自己的路径为负数
for (register int k = 1; k <= sum; k ++) {
register int tmp = 0;
for (register int i = 1; i <= n; i ++) {
for (register int j = 1; j <= n; j ++) {
if (belong [i] == k && belong[j] == k) {
tmp = max (tmp, f[i][j] + 1);
}
}
}
ans += tmp;
}
printf ("%d
", ans);
return 0;
}