「NOIP」 联赛模拟测试33

合并集合

不会的建议直接重学 区间(dp)。

跟石子合并很像，发现 (n) 很小，直接 (n^3) 预处理贡献就行了，然后直接 (dp)，懒得讲了。

小声bb：考试的时候，20分钟打完正解，为了对拍，暴力打了40分钟/kk

代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 6e2 + 50, INF = 0x3f3f3f3f;

inline int read () {
	register int x = 0, w = 1;
	register char ch = getchar ();
	for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
	for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
	return x * w;
}

inline void write (register int x) {
	if (x / 10) write (x / 10);
	putchar (x % 10 + '0');
}

int n, ans;
int a[maxn], f[maxn][maxn], num[maxn][maxn];
bool vis[maxn];

int main () {
	freopen ("merge.in", "r", stdin);
	freopen ("merge.out", "w", stdout);
	n = read();
	for (register int i = 1; i <= n; i ++) a[i] = a[i + n] = read();
	for (register int d = 1; d <= n; d ++) {
		for (register int i = 1, j; (j = i + d - 1) <= 2 * n; i ++) {
			memset (vis, 0, sizeof vis);
			for (register int k = i; k <= j; k ++) {
				if (! vis[a[k]]) num[i][j] ++, vis[a[k]] = 1;
			}
		}
	}
	for (register int d = 2; d <= n; d ++) {
		for (register int i = 1, j; (j = i + d - 1) <= 2 * n; i ++) {
			for (register int k = i; k < j; k ++) {
				f[i][j] = max (f[i][j], f[i][k] + f[k + 1][j] + num[i][k] * num[k + 1][j]);
			}
		}
	}
	for (register int i = 1, j; (j = i + n - 1) <= 2 * n; i ++) ans = max (ans, f[i][j]);
	printf ("%d
", ans);
	return 0;
}

ZYB建围墙

一看数据范围 (1e9) 和简单的输入输出，很明显是个数学题，考场上找了 (1) 个半小时的规律，没有头绪，想到某略日，果断放弃。

想起来还是比较简单的。

很显然，放的越紧凑，公共边越多，最后的答案是越小的。

所以我们先考虑把大部分放成如下形状：

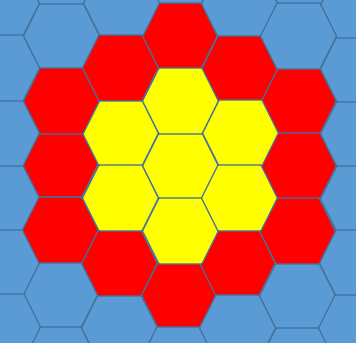
剩下的单个的再绕着周围放，可以贪心一下放，建议自己手摸。

代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int maxn = 1e5 + 50, INF = 0x3f3f3f3f;

inline int read () {
	register int x = 0, w = 1;
	register char ch = getchar ();
	for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
	for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
	return x * w;
}

inline void write (register int x) {
	if (x / 10) write (x / 10);
	putchar (x % 10 + '0');
}

int n, d, ans;
int f[maxn];

inline void Init () {
	for (register int i = 0; i <= n; i ++) {
		f[i] = 6 * (i + 1) * i / 2 + 1;
		if (f[i] > n) {
			d = i, n -= f[i - 1], ans += f[i] - f[i - 1]; break;
		}
	}	
}

int main () {
	freopen ("wall.in", "r", stdin);
	freopen ("wall.out", "w", stdout);
	n = read(), Init ();
	if (n) ans += (n / d + 1);
	printf ("%d
", ans);
	return 0;
}

ZYB和售货机

直接贪心可以搞到 (40; pts) 。

如果我们对于每个 (i)，向它的 (f[i]) 建边，会发现是一个类似基环森林的东西。

我们先利用一下贪心的思想，把能取的都取了，使每个都剩下一个，这样既能做到贡献最大，又可以不会对接下来的选择造成影响，所以这个策略是正确的。

接下来所有的物品就剩下了 (1) 个。

考虑上面那个图：

• 对于链的情况，显然一条链选下去所有的价值都可以选上。

• 对于一个环（没有链与之相连），一定会有一个点的贡献选不到，求和减去最小的即可。

但是，上面那个图的边太多了，考虑简化：

如果说，我们选一个成本最小的儿子向它建边，一个点的入度和出度都不会超过 (1)，只会剩下单独的链和环，就好做了。

但是，很容易发现这样做的正确性是不对的，比如下面这个样例：

3
2 2 10 1
3 2 8 1
2 1 9 1

我们按上面的方法建出图来后，只会有 (2) 和 (3) 的一个环，求出来是 (7) 。

显然我们可以先选 (2)，再选 (1)，使我们的答案为 (13) 。

所以，我们对每个环上的点考虑一下它所有儿子中的次小值，即贡献第二小的点，比如：

(5) 是 (4) 贡献第二大的点，(3) 是 (4) 贡献第一大的点，由于选完 (3) 不能选 (4) 的影响，会有两种决策：

• 选了 (3) 而不能选 (4) 和 (5) 。

• 选了 (5) 和 (4) 而不能选 (3) 。

所以两种情况取个最大值即可。

代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>

typedef long long ll;

using namespace std;

const int maxn = 1e5 + 50, INF = 0x3f3f3f3f;

inline int read () {
	register int x = 0, w = 1;
	register char ch = getchar ();
	for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
	for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
	return x * w;
}

inline void write (register int x) {
	if (x / 10) write (x / 10);
	putchar (x % 10 + '0');
}

int n;
ll ans;

struct Edge {
	int to, next;
} e[maxn << 1];

int tot, head[maxn];

inline void Add (register int u, register int v) {
	e[++ tot].to = v;
	e[tot].next = head[u];
	head[u] = tot;
}

struct Node {
	int id, val;
	Node () {}
	Node (register int a, register int b) { id = a, val = b; }
	inline bool operator < (const Node &x) const { return val < x.val; }
};

int f[maxn], c[maxn], d[maxn], a[maxn], val[maxn], val2[maxn];

vector <Node> vec[maxn];
priority_queue <Node> q;

bool vis[maxn];
int dfn[maxn], low[maxn], size[maxn], belong[maxn], maxx[maxn], st[maxn], deg[maxn], rdeg[maxn];
ll totval[maxn];
int tic, top, sum;

inline void Tarjan (register int u) {
	dfn[u] = low[u] = ++ tic, st[++ top] = u, vis[u] = 1;
	for (register int i = head[u]; i; i = e[i].next) {
		register int v = e[i].to;
		if (! dfn[v]) {
			Tarjan (v);
			low[u] = min (low[u], low[v]);
		} else if (vis[v]) {
			low[u] = min (low[u], dfn[v]);
		}
	}
	if (dfn[u] == low[u]) {
		sum ++;
		while (st[top + 1] != u) {
			register int v = st[top --];
			size[sum] ++, rdeg[sum] += deg[v];
			belong[v] = sum;
			if (vec[v].size ()) maxx[sum] = max (maxx[sum], val2[v] - val[vec[v][vec[v].size () - 1].id]);
			if (deg[v]) totval[sum] += val[v];
			vis[v] = 0;
		}
	}
}

int main () {
	freopen ("goods.in", "r", stdin);
	freopen ("goods.out", "w", stdout);
	n = read(), memset (maxx, - 0x3f, sizeof maxx);;
	for (register int i = 1; i <= n; i ++) f[i] = read(), c[i] = read(), d[i] = read(), a[i] = read();
	for (register int i = 1; i <= n; i ++) val[i] = d[f[i]] - c[i], vec[f[i]].push_back (Node (i, d[f[i]] - c[i])), q.push (Node (f[i], d[f[i]] - c[i]));
	while (! q.empty ()) {
		register Node t = q.top (); q.pop ();
		if (t.val <= 0) break;
		if (a[t.id] > 1) ans += 1ll * (a[t.id] - 1) * t.val, a[t.id] = 1;
	}
	for (register int i = 1; i <= n; i ++) {
		sort (vec[i].begin (), vec[i].end ());
		if (vec[i].empty ()) continue;
		register int end = vec[i].size () - 1;
		if (vec[i][end].val > 0) Add (vec[i][end].id, i), deg[vec[i][end].id] ++;
		if (vec[i].size () >= 2 && val[vec[i][end - 1].id] > 0) val2[i] = val[vec[i][end - 1].id];
	}
	for (register int i = 1; i <= n; i ++) if (! dfn[i]) Tarjan (i);
	for (register int i = 1; i <= sum; i ++) {
		if (size[i] == 1) ans += totval[i];
		else ans += totval[i] + maxx[i];
	}
	printf ("%lld
", ans);
	return 0;
}