前置知识
多项式
定义
在数学中,由若干个单项式相加组成的代数式叫做多项式(若有减法:减一个数等于加上它的相反数)。多项式中的每个单项式叫做多项式的项,这些单项式中的最高项次数,就是这个多项式的次数。其中多项式中不含字母的项叫做常数项。
——百度百科
对于一个含有未知数的式子,如下:
-
(x,y) 是这个式子里的未知数,叫作元。
-
(x^2,x,3) 是这个式子里的单项式,叫作项。
-
(^2) 是最高项次数,叫作次数。
表示
系数表示法
即用这个多项式的每一项系数来表示这个多项式。
一个 (n-1) 次 (n) 项多项式:
用系数表示法为:
点值表示法
在初中,我们学过一次函数 (y=kx+b) 和二次函数 (y=ax^2+bx+c),不管前面的 (y),它们都是一个多项式。
我们学过:
-
给定平面直角坐标系上的两点,我们可以确定一个一次函数 (y=kx+b) 。
-
给定平面直角坐标系上的三点,我们可以确定一个二次函数 (y=ax^2+bx+c) 。
以此类推,给定平面直角坐标系上的 (n) 个点,我们可以确定一个 (n-1) 次多项式。
所以,对于一个 (n-1) 次多项式,我们可以用 (n) 个点值来表示这个多项式。
复数
定义
我们把形如 (z=a+bi)((a,b) 均为实数)的数称为复数,其中 (a) 称为实部,(b) 称为虚部,(i) 称为虚数单位。当 (z) 的虚部等于零时,常称 (z) 为实数;当 (z) 的虚部不等于零时,实部等于零时,常称 (z) 为纯虚数。复数域是实数域的代数闭包,即任何复系数多项式在复数域中总有根。
复数是由意大利米兰学者卡当在十六世纪首次引入,经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作,此概念逐渐为数学家所接受。
——百度百科
在实数范围内 (sqrt{-1}) 是不存在的,但是在复数中,我们定义 (i^2=-1) 。
也许有些难理解,不妨将一个复数看作平面直角坐标系某个一次函数上的一个点,只不过这个坐标系有些特殊,横轴是实部,纵轴是虚部。
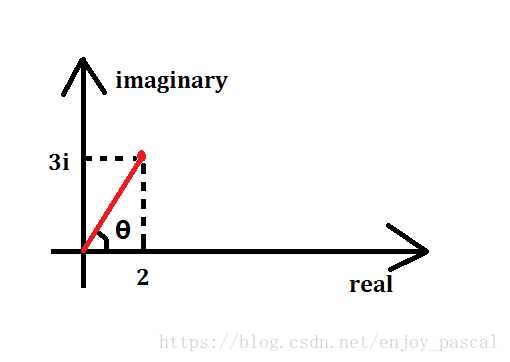
图中表示的就是一个复数 (2 + 3i) 。
(PS):如果你把他当成向量来理解也没问题。
极角
复数在坐标系上与原点的连线和横轴所成的夹角,即上图的 ( heta) 。
模
复数的模就是它到坐标远点的距离:
共轭复数
一个复数的共轭复数就是它虚部取反的复数:
运算
设 (z_1=a+bi,z_2=c+di)
加法
复数的加法类似于向量相加,并且满足平行四边形法则:

减法
乘法
性质:模长相乘,极角相加。
DFT (离散傅里叶变换)
在数学上,我们通常用于将一个 (n) 次多项式从系数表示法转为点值表示法。
最朴素的方法是,随便代入若干个不同的 (x),用 (Theta (n)) 的效率求出点值,总复杂度 (Theta (n^2)) 。
如果我们代入一组特殊的 (x),使 (x) 的若干次方都为 (1),我们可以很容易计算。
但是在实数范围内,只有 (1) 的若干次方都为 (1),是远远不够的。
但是如果我们引入复数,就会有很多数符合这个条件,傅里叶说:“下面圆上的点都能满足这个条件”。

不妨将其等分成 (n=8) 份,将这些点代入到多项式中。
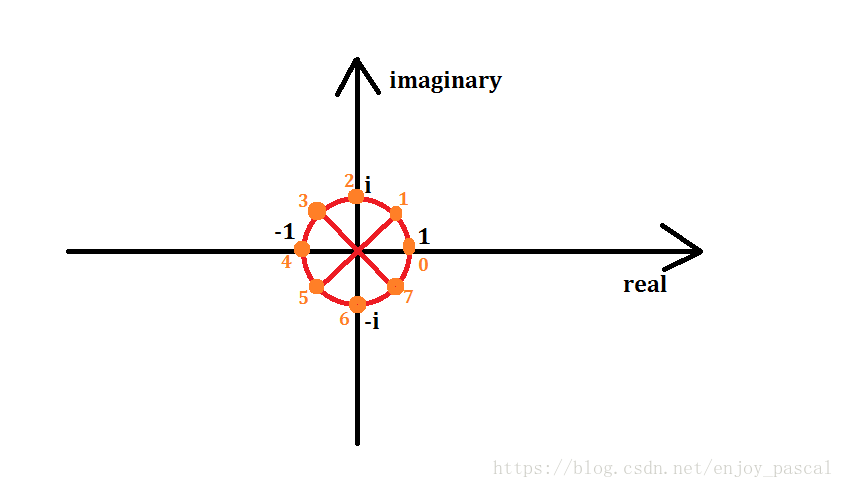
单位根
我们将上面圆上的点所代表的复数叫作单位根,用 (w_n^k) 表示,(n) 表示圆分成的份数,且通常是 (2) 的次幂,(k) 表示逆时针数第 (k) 个点。
(w_n^1) 称为 (n) 次单位根。
性质
- ((w_n^1)^k=w_n^k),由复数的乘法性质“模长相乘,极角相加”易证。
- (w_n^k=cosfrac{k}{n}2pi+isinfrac{k}{n}2pi),下图易证:
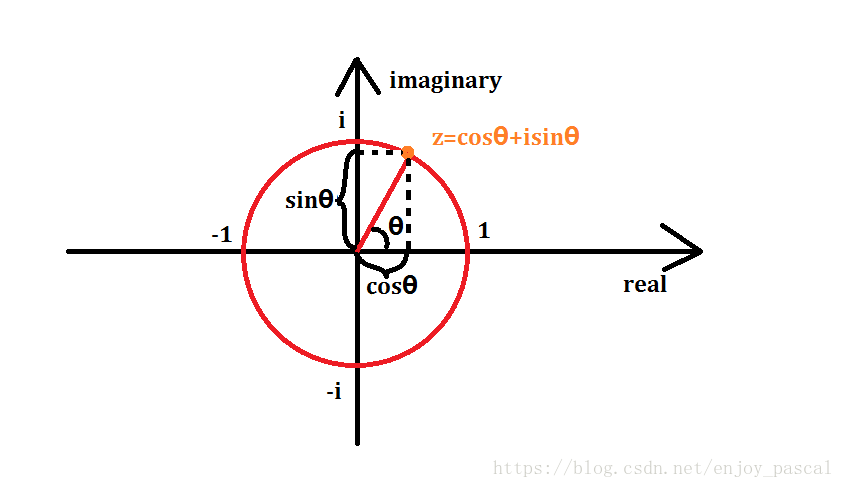
- (w_n^k=w_{2n}^{2k}),证明:
- (w_n^{k+frac{2}{n}}=-w_{n}^{k}),证明:
- (w_n^0=w_n^n),证明:
FFT (快速傅里叶变换)
我们用 (DFT) 计算出一些 (w) 值来代替 (x) 进行计算,但还是要暴力代入计算,复杂度还是 (Theta (n^2))...
(FFT) 让我们的 (DFT) 可以分治来做,从而使时间复杂度达到喜人的 (Theta(nlog^n)) 。
设多项式
设多项式
得
设 (k<frac{n}{2}) 然后将 (w_n^k) 作为 (x) 代入
证毕
所以,我们只要知道了 (A_1(w_frac{n}{2}^k)) 和 (A_2(w_frac{n}{2}^k)) 的值,我们就可以求 (A(w_n^k)) 和 (A(w_n^{k+frac{n}{2}})) 的值,我们就可以分治地将多项式系数表示法转化成点值表示法。
IFFT (快速傅里叶逆变换)
我们现在已经会了将多项式系数表示法转化成点值表示法,但是怎么转化回去呢?
傅里叶告诉我们一个结论:
一个多项式在分治的过程中乘上单位根的共轭复数,分治完的每一项除以 (n) 即为原多项式的每一项系数。
所以我们只需 (FFT) 中 (w) 的虚部乘上 (-1),并且最后将每个值除以 (n) 即可。
关于 FFT & IFFT 的小细节
-
(n) 的值只能取 (2) 的次幂,因为我们在定义 (w_n^k) 时,已经限制了这个条件了。
-
当递归分治到 (n=1) 时,只有常数项,直接 (return) 。
递归 FFT 代码
inline void FFT (register int len, register Complex * a, register int opt) { // opt=1时是FFT,opt=-1时是IFFT
if (len == 1) return; // 项数为1,只有常数项,直接返回
register Complex a1[len >> 1], a2[len >> 1];
for (register int i = 0; i <= len - 1; i += 2) //根据下标的奇偶分开
a1[i >> 1] = a[i], a2[i >> 1] = a[i + 1];
FFT (len >> 1, a1, opt), FFT (len >> 1, a2, opt); // 分治递归
register Complex w1 = Complex (opt * sin (2.0 * pi / len), cos (2.0 * pi / len)); // w_n^1
register Complex w = Complex (0, 1); // w_n^0
len >>= 1;
for (register int i = 0; i <= len - 1; i ++, w = w * w1)
a[i] = a1[i] + w * a2[i], a[i + len] = a1[i] - w * a2[i];
}
多项式乘法
容易发现,用系数表示法来相乘,复杂度是 (Theta(n^2)) 的。
但是,转成两个点值表示法来求,复杂度是 (Theta(n)) 的。
设
相乘得
所以,我们可以用 (FFT) 将两个多项式转化成点值表达式,然后 (Theta(n)) 相乘,再用 (IFFT) 转成系数表达式。
代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn = 6e6 + 50, INF = 0x3f3f3f3f;
const double pi = acos (- 1.0);
inline int read () {
register int x = 0, w = 1;
register char ch = getchar ();
for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
return x * w;
}
inline void write (register int x) {
if (x / 10) write (x / 10);
putchar (x % 10 + '0');
}
int n, m, len = 1;
struct Complex { // 复数,也可以用自带的complex库
double x, y; // 虚部,实部
Complex () { x = y = 0; }
Complex (register double a, register double b) { x = a, y = b; }
inline Complex operator + (const Complex &a) const { return Complex (x + a.x, y + a.y); }
inline Complex operator - (const Complex &a) const { return Complex (x - a.x, y - a.y); }
inline Complex operator * (const Complex &a) const { return Complex (x * a.y + y * a.x, y * a.y - x * a.x); }
} a[maxn], b[maxn];
inline void FFT (register int len, register Complex * a, register int opt) { // opt=1时是FFT,opt=-1时是IFFT
if (len == 1) return; // 项数为1,只有常数项,直接返回
register Complex a1[len >> 1], a2[len >> 1];
for (register int i = 0; i <= len - 1; i += 2) //根据下标的奇偶分开
a1[i >> 1] = a[i], a2[i >> 1] = a[i + 1];
FFT (len >> 1, a1, opt), FFT (len >> 1, a2, opt); // 分治递归
register Complex w1 = Complex (opt * sin (2.0 * pi / len), cos (2.0 * pi / len)); // w_n^1
register Complex w = Complex (0, 1); // w_n^0
len >>= 1;
for (register int i = 0; i <= len - 1; i ++, w = w * w1)
a[i] = a1[i] + w * a2[i], a[i + len] = a1[i] - w * a2[i];
}
int main () {
n = read(), m = read();
for (register int i = 0; i <= n; i ++) a[i].y = read();
for (register int i = 0; i <= m; i ++) b[i].y = read();
while (len <= n + m) len <<= 1; // 项数只能是2的次幂,所以找到第一个大于n+m的即可
FFT (len, a, 1), FFT (len, b, 1); // 系数转点值
for (register int i = 0; i <= len - 1; i ++) a[i] = a[i] * b[i]; // 点值多项式相乘
FFT (len, a, -1); // 点值转系数
for (register int i = 0; i <= n + m; i ++) printf ("%d ", (int) (a[i].y / len + 0.5));
putchar ('
');
return 0;
}
迭代优化
递归的效率太差了,所以我们需要一点小优化。

我们会发现,分治后的位置,是其下标二进制翻转以后的位置,我们可以先预处理好它最后到达的位置,在 (FFT) 之前交换即可。
迭代 FFT 代码
inline void FFT (register int len, register Complex *a, register int opt) {
for (register int i = 1; i < len; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << bit - 1); // 预处理
for (register int i = 0; i < len; i ++) if (i < rev[i]) swap (a[i], a[rev[i]]); // 提前交换位置
for (register int d = 1; d < len; d <<= 1) { // 当前变换所得序列的一半
register Complex w1 = Complex (opt * sin (pi / d), cos (pi / d)); // 2*pi与2*d消掉了一个2
for (register int i = 0; i < len; i += d * 2) { // 对每一段进行变换
register Complex w = Complex (0, 1);
for (register int j = 0; j < d; j ++, w = w * w1) {
register Complex x = a[i + j], y = w * a[i + j + d]; // 蝴蝶变换
a[i + j] = x + y, a[i + j + d] = x - y;
}
}
}
}
(PS):网上有些三次 (FFT) 变两次 (FFT) 的做法,但是这让本来精度就不好的 (FFT) 更加雪上加霜,一般不怎么用,其实是我也不会。
NTT (快速数论变换)
容易发现,我们用 (FFT) 进行多项式乘法时引入了复数单位根,从而便于了计算,但是用的是 (double) 类型,精度可能会出问题,或许我们能找到某个东西来代替单位根。
阶
设 (a,p) 是整数,(a) 和 (p) 互质,那么:
使 (a^nequiv 1mod p) 成立的最小正整数 (n) 叫做 (a) 模 (p) 的阶,记作 (delta_p(a)=n) 。
——百度百科
例如:
原根
设 (m) 是正整数,(a) 是整数,若 (a) 模 (m) 的阶等于 (phi (m)),则称 (a) 为模 (m) 的一个原根。
——百度百科
具体原根性质详见百度百科,这里我们只用到了基本定义。
对于一个模数 (p),设它的原根为 (g),则有:
若 (p) 为质数,则有:
根据单位根的性质,有:
这样我们就能够用原根来代替单位根了。
NTT 代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
typedef long long ll;
using namespace std;
const int maxn = 3e6 + 50, INF = 0x3f3f3f3f, mod = 998244353;
inline int read () {
register int x = 0, w = 1;
register char ch = getchar ();
for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
return x * w;
}
inline void write (register int x) {
if (x / 10) write (x / 10);
putchar (x % 10 + '0');
}
int n, m, len = 1, bit, rev[maxn];
ll a[maxn], b[maxn];
inline ll qpow (register ll a, register ll b) {
register ll ans = 1;
while (b) {
if (b & 1) ans = ans * a % mod;
a = a * a % mod, b >>= 1;
}
return ans;
}
inline void NTT (re板子gister int len, register ll * a, register ll opt) {
for (register int i = 1; i <= len; i ++) if (i < rev[i]) swap (a[i], a[rev[i]]);
for (register int d = 1; d < len; d <<= 1) {
register ll w1 = qpow (opt, (mod - 1) / (d << 1));
for (register int i = 0; i < len; i += d << 1) {
register ll w = 1;
for (register int j = 0; j < d; j ++, w = w * w1 % mod) {
register ll x = a[i + j], y = w * a[i + j + d] % mod;
a[i + j] = (x + y) % mod, a[i + j + d] = (x - y + mod) % mod;
}
}
}
}
int main () {
n = read(), m = read();
while (len <= n + m) len <<= 1, bit ++;
for (register int i = 0; i <= n; i ++) a[i] = read();
for (register int i = 0; i <= m; i ++) b[i] = read();
for (register int i = 1; i <= len; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << bit - 1);
NTT (len, a, 3), NTT (len, b, 3);
for (register int i = 0; i <= len; i ++) a[i] = a[i] * b[i] % mod;
NTT (len, a, qpow (3, mod - 2));
for (register int i = 0; i <= n + m; i ++) printf ("%lld ", a[i] * qpow (len, mod - 2) % mod); putchar ('
');
return 0;
}