前缀+排序 HDOJ 4311 Meeting point-1

题目传送门

题意：给一些坐标轴上的点，选一个点，使得其他点到该点曼哈顿距离和最小

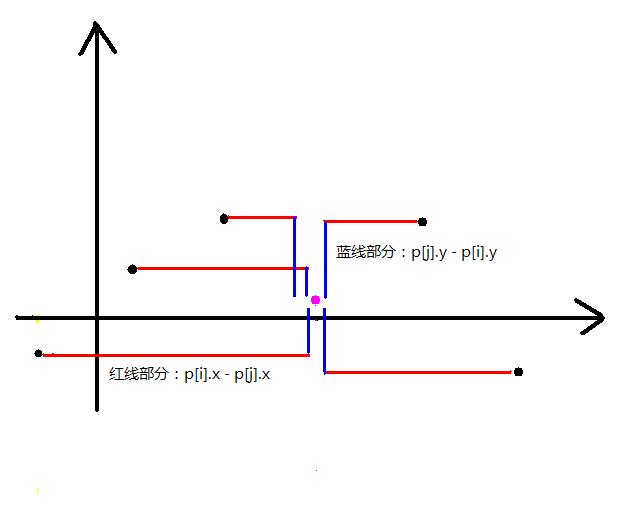
分析：这题有很强的技巧性，直接计算每个点的曼哈顿距离和是不可行的。这里用到了前缀的思想，先对点按照x从左到右排序，p[i].sum保存选择i点时曼哈顿距离和是多少，p[i].sum = (i - 1) * p[i].x - sum (p1.x~pi-1.x) + sum (pi+1.x~pn.x) - (n - i) * p[i].x; ，i前面每个点的到i的x轴距离为：p[i].x - p[j].x，i后面每个点到i的x轴距离为：p[j].x - p[i].x，累计求和就是上式，y轴同理，可能配上图好理解：

那么每个点都计算出来了，只要在遍历一遍取最小值就是答案

收获：1. 前缀的使用技巧 2. 还有升级版的？

代码：

/************************************************
* Author        :Running_Time
* Created Time  :2015-8-24 13:21:56
* File Name     :B_2.cpp
 ************************************************/

#include <cstdio>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cstring>
#include <cmath>
#include <string>
#include <vector>
#include <queue>
#include <deque>
#include <stack>
#include <list>
#include <map>
#include <set>
#include <bitset>
#include <cstdlib>
#include <ctime>
using namespace std;

#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
typedef long long ll;
const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
const ll INFF = 1ll << 62;
const int MOD = 1e9 + 7;
struct Point	{
	ll x, y, sum;
}p[N];
int n;

bool cmpx(Point a, Point b)	{
	return a.x < b.x;
}

bool cmpy(Point a, Point b)	{
	return a.y < b.y;
}

int main(void)    {
	int T;	scanf ("%d", &T);
	while (T--)	{
		scanf ("%d", &n);
		for (int i=1; i<=n; ++i)	{
			scanf ("%I64d%I64d", &p[i].x, &p[i].y);
		}
		sort (p+1, p+1+n, cmpx);	ll sum = 0;
		for (int i=1; i<=n; ++i)	{
			p[i].sum = (i - 1) * p[i].x - sum;
			sum += p[i].x;
		}
		sum = 0;
		for (int i=n; i>=1; --i)	{
			p[i].sum += sum - (n - i) * p[i].x;
			sum += p[i].x;
		}

		sort (p+1, p+1+n, cmpy);	sum = 0;
		for (int i=1; i<=n; ++i)	{
			p[i].sum += (i - 1) * p[i].y - sum;
			sum += p[i].y;
		}
		sum = 0;
		for (int i=n; i>=1; --i)	{
			p[i].sum += sum - (n - i) * p[i].y;
			sum += p[i].y;
		}

		ll ans = INFF;
		for (int i=1; i<=n; ++i)	{
			ans = min (ans, p[i].sum);
		}
		printf ("%I64d
", ans);
	}

    return 0;
}