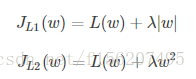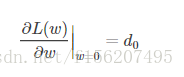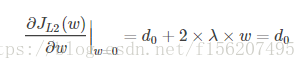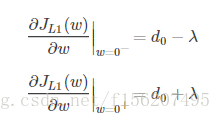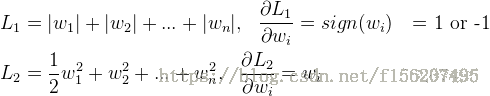原文:https://blog.csdn.net/f156207495/article/details/82794151
问题
为什么L1正则化较容易产生稀疏解,而L2正则化较平缓稳定
- 1
介绍L1和L2
L1和L2正则常被用来解决过拟合问题。而L1正则也常被用来进行特征选择,主要原因在于L1正则化会使得较多的参数为0,从而产生稀疏解。我们可以将0对应的特征遗弃,进而用来选择特征。
角度一 ——从代价函数上来看
但为什么L1正则会产生稀疏解呢?这里利用公式进行解释。
假设只有一个参数为w,损失函数为L(w),分别加上L1正则项和L2正则项后有:
假设L(w)在0处的倒数为d0,即
则可以推导使用L1正则和L2正则时的导数。
引入L2正则项,在0处的导数
引入L1正则项,在0处的导数
可见,引入L2正则时,代价函数在0处的导数仍是d0,无变化。而引入L1正则后,代价函数在0处的导数有一个突变。从d0+λ到d0−λ,若d0+λ和d0−λ异号,则在0处会是一个极小值点。因此,优化时,很可能优化到该极小值点上,即w=0处。
这里只解释了有一个参数的情况,如果有更多的参数,也是类似的。因此,用L1正则更容易产生稀疏解。
角度二 ——L1正则化本身的导数性质
这个角度从权值的更新公式来看权值的收敛结果。
首先来看看L1和L2的梯度(导数的反方向):
所以(不失一般性,我们假定:wi等于不为0的某个正的浮点数,学习速率η 为0.5):
L1的权值更新公式为wi = wi - η * 1 = wi - 0.5 * 1,也就是说权值每次更新都固定减少一个特定的值(比如0.5),那么经过若干次迭代之后,权值就有可能减少到0。
L2的权值更新公式为wi = wi - η * wi = wi - 0.5 * wi,也就是说权值每次都等于上一次的1/2,那么,虽然权值不断变小,但是因为每次都等于上一次的一半,所以很快会收敛到较小的值但不为0。
下面的图很直观的说明了这个变化趋势:
L1能产生等于0的权值,即能够剔除某些特征在模型中的作用(特征选择),即产生稀疏的效果。
L2可以得迅速得到比较小的权值,但是难以收敛到0,所以产生的不是稀疏而是平滑的效果。
角度三 ——几何空间
这个角度从几何位置关系来看权值的取值情况。
直接来看下面这张图
高维我们无法想象,简化到2维的情形,如上图所示。其中,左边是L1图示,右边是L2图示,左边的方形线上是L1中w1/w2取值区间,右边得圆形线上是L2中w1/w2的取值区间,绿色的圆圈表示w1/w2取不同值时整个正则化项的值的等高线(凸函数),从等高线和w1/w2取值区间的交点可以看到,L1中两个权值倾向于一个较大另一个为0,L2中两个权值倾向于均为非零的较小数。这也就是L1稀疏,L2平滑的效果。
参考
https://vimsky.com/article/969.html
https://blog.csdn.net/b876144622/article/details/81276818
https://blog.csdn.net/liangdong2014/article/details/79517638