需要排序的数据文件太大,导致数据不能全部存入内存,要如何进行排序呢?这就是外部排序解决的问题。
相比其他排序算法,这个排序用到了操作系统的一些知识,算法过程让人不禁感叹“这才是计算机科学啊”。
Divide and conquer: sort subfiles and merge
分而治之:对子文件进行排序并合并
置换与最佳归并树
https://wenku.baidu.com/view/8b3f09322af90242a895e554.html
算法实现
https://zhuanlan.zhihu.com/p/36618960
以下是我学习外部排序过程中认为讲解最形象清楚的一篇推文~
背景
西天取经的路上,一样上演着编程的乐趣.....



(互联网侦察注:160亿字节大概是16G吧,20亿int32大概8G)



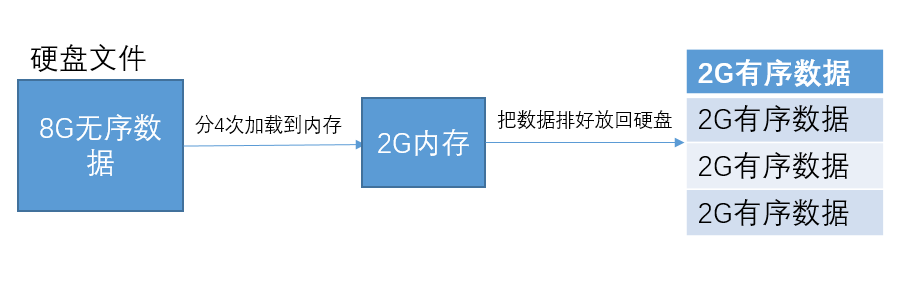
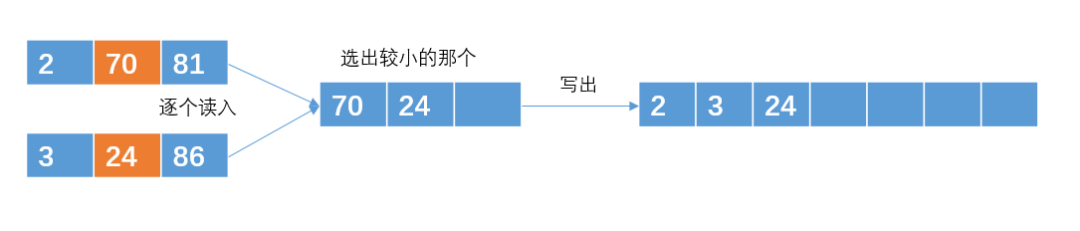
排序的时候我们可以选择快速排序或归并排序等算法。为了方便,我们把排序好的2G有序数据称之为有序子串吧。接着我们可以把两个小的有序子串合并成一个大的有序子串。

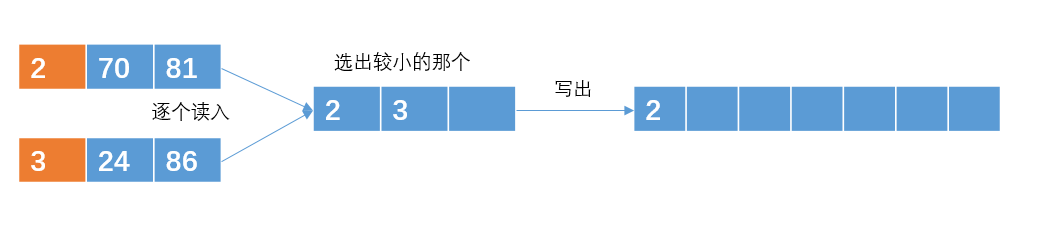
注意:读取的时候是每次读取一个int数,通过比较之后在输出。
按照这个方法来回合并,总共经过三次合并之后就可以得到8G的有序子串。



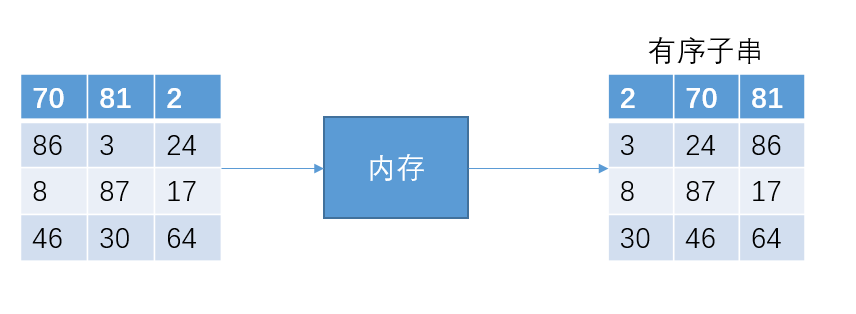
接下来把12个数据分成4份,然后排序成有序子串
然后把子串进行两两合并
输出哪个元素,就在那个元素所在的有序子串再次读入一个元素
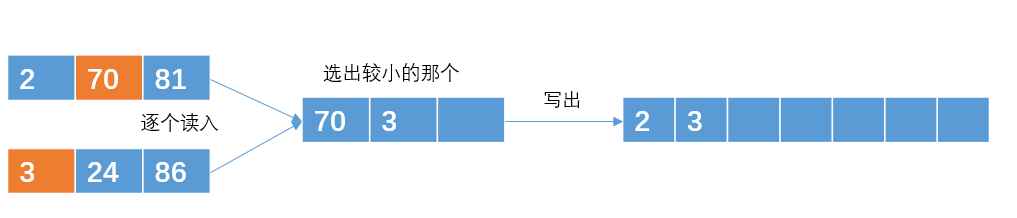
继续
重复直到合并成一个包含6个int的有序子串

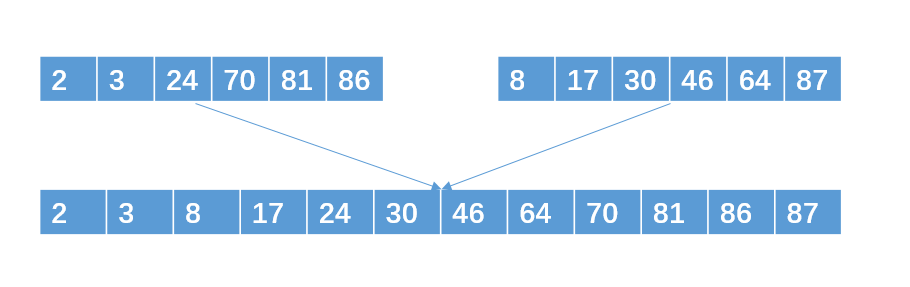
再把两个包含6个int的有序子串合并成一个包含12个int数据的最终有序子串

优化策略

解释下:例如对于数据2,我们把无序的12个数据分成有序的4个子串需要读写各一次,把2份3个有序子串合并成6个有序子串读写各一次;把2份6个有序子串合并从12个有序子串读写各一次,一共需要读写各3次。



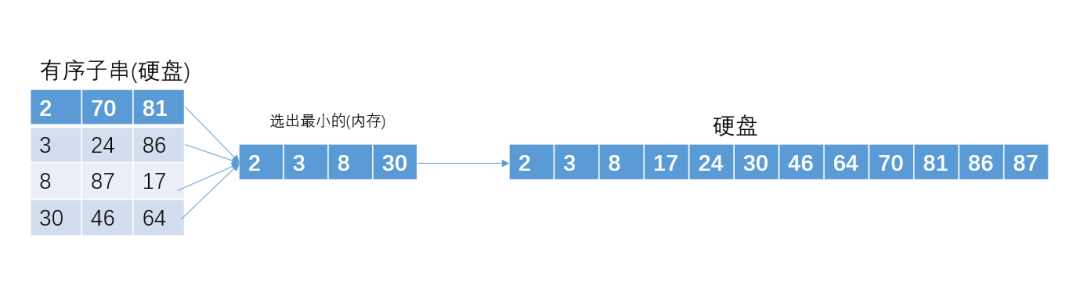
多路归并
为了方便讲解,我们假设内存一共可以装4个int型数据。






置换选择







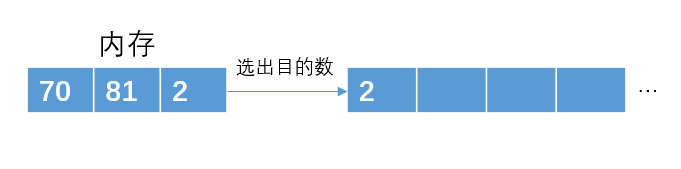
例如我们可以从12个数据读取3个存到内存中,然后从内存中选出最小的那个数放进子串p1里;
之后再从在从剩余的9个数据读取一个放到内存中,然后再从内存中选出一个数放进子串p1里,这个数必须满足比p1中的其他数大,且在内存中尽量小。
这样一直重复,直到内存中的数都比p1中的数小,这时p1子串存放结束,继续来p2子串的存放。例如(这时假设内存只能存放3个int型数据):
12个无序的int数据

读入3个到内存中,且选出一个最小的到子串p1
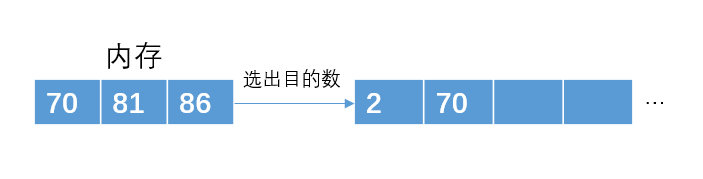
从内存中再次读取一个元素86
从内存中再次读取一个元素3
从内存中再次读取一个元素24
从内存中再次读取一个元素8
这个时候,已经没有符合要求的数了,且内存已满,进而用p2子串来存放,以此类推。
通过这种方法,p1子串存放了4个数据,而原来的那种方法p1子串只能存放3个数据。


(不知道堆排序的可以看下我之前写的文章:【算法与数据结构】堆排序是什么鬼?)
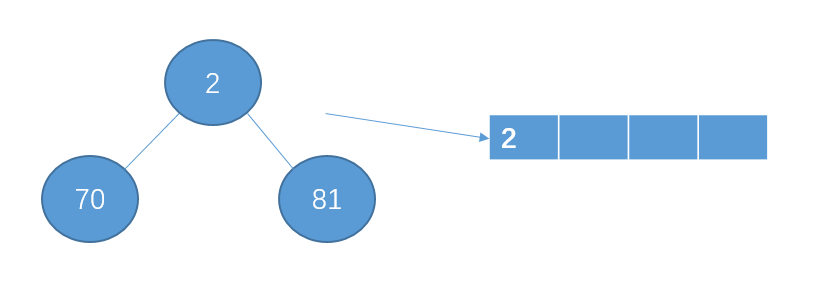
从12个数据中读取3个数据,构建成一个最小堆,然后从堆顶选择一个数写入到p1中。
之后再从剩余的9个数中读取一个数,如果这个数比刚才那个写入到p1中的数大,则把这个数插入到最小堆中,重新调整最小堆结构,然后在堆顶选一个数写入到p1中。
否则,把这个数暂放在一边,暂时不处理。之后一样需要调整堆结构,从堆顶选择一个数写入到p1中。
这里说明一下,那个被放在一边的数是不能再放入p1中的了,因为它一定比p1中的数都要小,所以它会放在下一个子串中
看这些文字会让人头大,我画图解释下吧。
从12数据读取3个数据

构建最小堆,且选出目标数
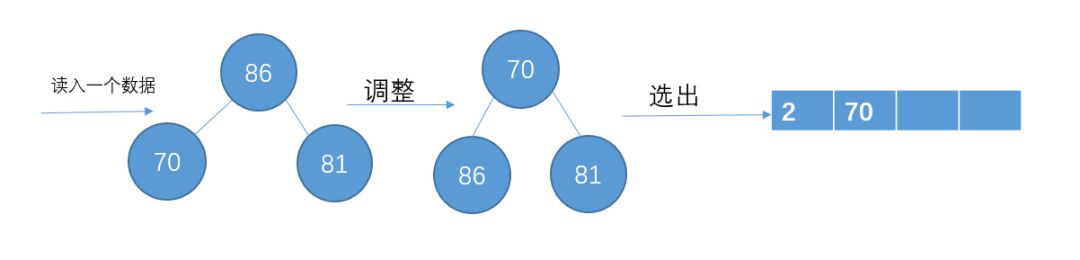
读入下一个数86
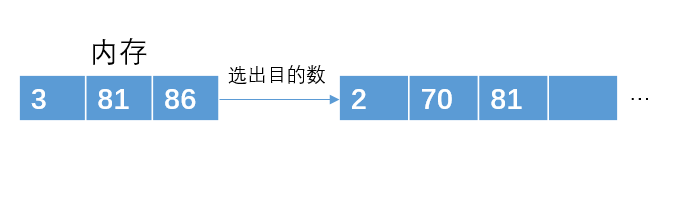
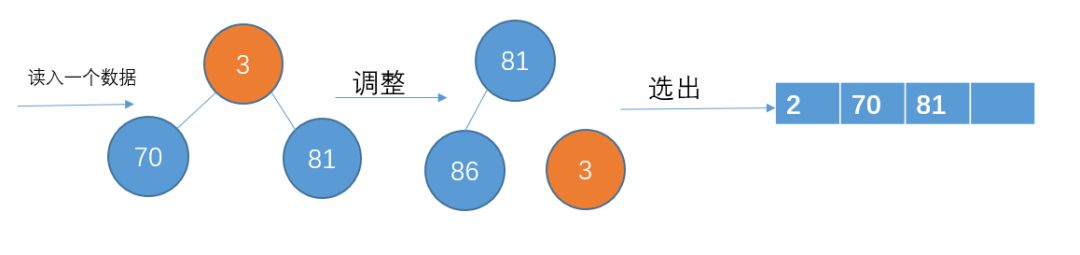
读入下一个数3,比70小,暂放一边,不加入堆结构中
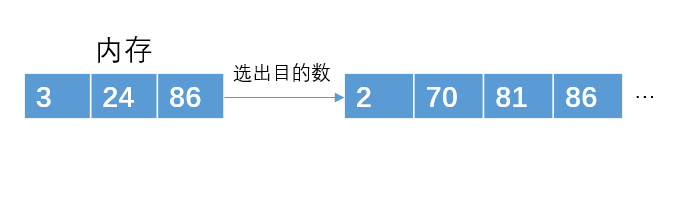
读入下一个数据24,比81小,不加入堆结构
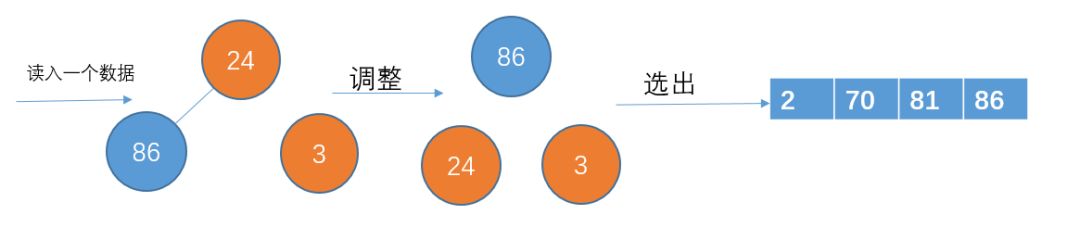
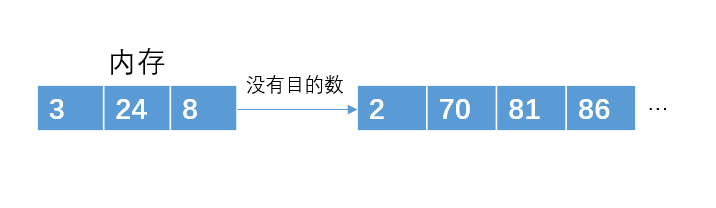
读入下一个数据8,比86小,不加入堆结构。此时p1已经完成了,把那些刚才暂放一边的数重新构成一个堆,继续p2的存放。
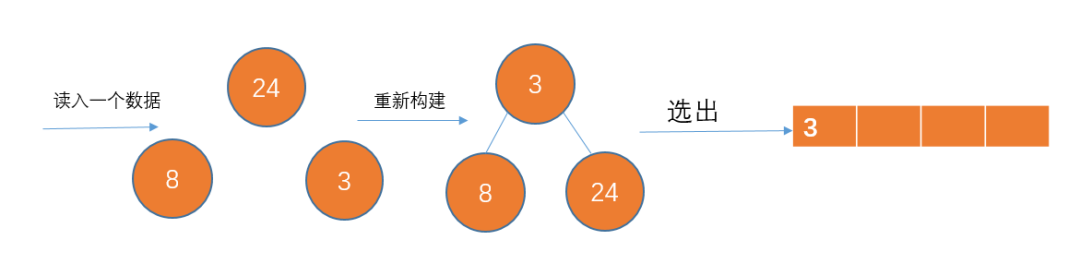
以此类推...
最后生成的p2如下:
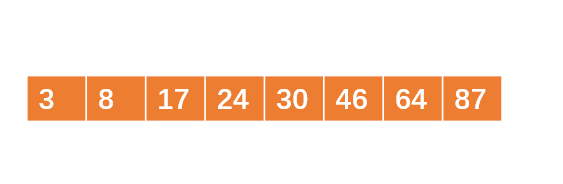



(互联网侦察注:这里作者笔误,应该是2n)

这种方法适合要排序的数据太多,以至于内存一次性装载不下。只能通过把数据分几次的方式来排序,我们也把这种方法称之为外部排序