RGB 3通道卷积
推荐一个链接(用Excel实现多种维度的卷积):https://medium.com/apache-mxnet/multi-channel-convolutions-explained-with-ms-excel-9bbf8eb77108
其中3维卷积是这样的:
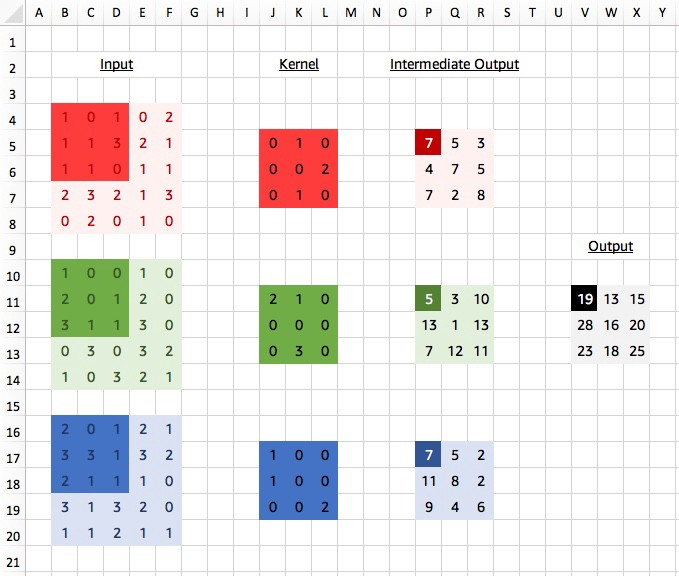
我以前的错误理解:如果输出通道只有1个,那么就只有1个卷积核(例如3x3,也就是9个参数)。然后该卷积核对输入3通道分别卷积,得到3张特征图,pixel-wise相加即可。
错误的地方:如果输入是RGB 3通道,那么就有3个卷积核!实际上有3x3x3=27个参数。
PyTorch的官方文档验证了这一点:

其中weight不仅与输出通道index有关,还与输入通道index有关。即,如果有inC个输入通道,inO个输出通道,那么就有inC x inO个卷积核(也就是权重矩阵)。
3D卷积
3D卷积的卷积核有3个维度。在上面的2D卷积中,输入通道数为3,就相当于完成了一次卷积核尺寸为(3,3,3)的3D卷积。
显然,3D卷积增加了灵活度:我们可以要求3D卷积核尺寸为(3,3,2),那么就会产生2个输出通道(1和2通道产生1个,2和3通道产生1个),而不再是像2D卷积一样恒输出一个通道。
而且3D卷积参数相对较小?因为这个3D核不断在复用。
合理性:比如处理视频帧,每一帧的编码逻辑是一样的,因此用相同的卷积核有合理性。
空洞卷积
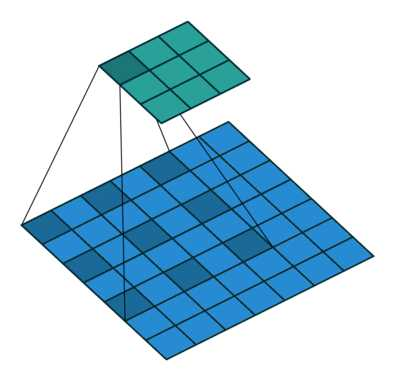
空洞的目的是捕捉long-term依赖,略微克服local conv的局限性。
根据MixConv报告,这种空洞卷积的空洞不能太大(不能超过2),否则会导致性能剧降。可能的原因是过于空洞导致local信息比较残缺。