闲扯
先看看了B组,T1 ZROI刚好讲过一个性质原根一般很小的,直接枚举;T2一眼二分然后似乎状压 T3没看
然后上来A组题,T1 flow这名字...网络流?!
T1题面非常的社会主义核心价值观,看到有个(m==n)的限制就想如果去掉怎么样,发现一棵树的话答案是确定的,然后考虑加上那条多出来的边,发现答案还是不变的?!想了想好像确实是这样,你树边确定了环边根本不用管,判断有无解就是点值加起来是否为0.于是直接DFS扫一遍去掉环边再DFS一遍就好了
T2 题面1984还行 出题人小心啊 扫了一眼觉得好难告辞
T3 第一眼题面 woc!!求求你们给国家省点子弹,我觉得博客中贴出这题题面的也要被查睡标了
第二眼woc?!这不是雅礼集训讲过的原题吗?!还记得点思路就是预处理坐几班车最远可到达的地方,讲题人还提到了长链剖分
于是肛肛肛...结果死活没调出来...然后xxzh巨佬讲了一种更好写的暴力....感觉以后考试看到原题还是得想想有没有其他的思路
结果15+0+0 T1 TM 正负号打反了,又犯SB错误 心态崩了
T1 flow
分析
某div 2 F竟这么水(你还不是挂分了)
见闲扯
代码
/*
code by RyeCatcher
*/
inline char gc(){
static char buf[SIZE],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,SIZE,stdin),p1==p2)?EOF:*p1++;
}
#define gc getchar
template <class T>inline void read(T &x){
x=0;int ne=0;char c;
while((c=gc())>'9'||c<'0')ne=c=='-';x=c-48;
while((c=gc())>='0'&&c<='9')x=(x<<3)+(x<<1)+c-48;x=ne?-x:x;return ;
}
const int maxn=200005;
const int inf=0x7fffffff;
struct Edge{
int ne,to,id;
bool ok;
}edge[maxn<<2];
int h[maxn],num_edge=1;
inline void add_edge(int f,int to,int id){
edge[++num_edge].ne=h[f];
edge[num_edge].to=to;
edge[num_edge].id=id;
edge[num_edge].ok=0;
h[f]=num_edge;
}
int w[maxn];
struct Nico{
int x,y,id,dis;
}nico[maxn<<2];
struct QAQ{
int x,y,fff;
int xd,yd;
}yyy[maxn<<2];
int tot=0;
int n,m;
namespace fake{
ll ans=0;
bool vis[maxn];
int fa[maxn];
void gao_cyc(int now){//去非树边
int v;
vis[now]=1;
for(ri i=h[now];i;i=edge[i].ne){
v=edge[i].to;
if(v==fa[now])continue;
if(vis[v]){
edge[i].ok=edge[i^1].ok=1;
}
if(edge[i].ok)continue;
fa[v]=now;
gao_cyc(v);
}
return ;
}
void get_ans(int now){
int v,id=0;
for(ri i=h[now];i;i=edge[i].ne){
v=edge[i].to;
if(edge[i].ok)continue;
if(v==fa[now]){
id=edge[i].id;continue;
}
get_ans(v);
}
yyy[++tot].x=now,yyy[tot].y=fa[now];
yyy[tot].xd=-w[now],yyy[tot].yd=w[now];
yyy[tot].fff=id;
w[fa[now]]+=w[now];
return ;
}
void main(){
int x,y,a,b;
for(ri i=1;i<=n;i++){
ans+=w[i];
}
memset(vis,0,sizeof(vis));
if(ans==0)puts("Possible");
else{
puts("Impossible");
return ;
}
fa[1]=0;
gao_cyc(1);
get_ans(1);
for(ri i=1;i<=tot;i++){
x=yyy[i].x,y=yyy[i].y;
a=nico[yyy[i].fff].x,b=nico[yyy[i].fff].y;
//printf("%d %d %d %d
",x,y,a,b);
if(x==a&&y==b){
nico[yyy[i].fff].dis=-yyy[i].xd;
}
else if(x==b&&y==a){
nico[yyy[i].fff].dis=-yyy[i].yd;
}
}
for(ri i=1;i<=m;i++){
printf("%d
",-nico[i].dis);
}
return ;
}
}
int main(){
int x,y;
FO(flow);
read(n);
for(ri i=1;i<=n;i++)read(w[i]);
read(m);
for(ri i=1;i<=m;i++){
read(x),read(y);
add_edge(x,y,i);
add_edge(y,x,i);
nico[i].x=x,nico[i].y=y,nico[i].dis=0;
}
//if(m<=20&&n<=20)bf::main();
fake::main();
return 0;
}
T2 moon
咕
T3 car
- 前置技能点
- 倍增
- 扫描线
- dfs序
预处理每个点在一条链上坐(2^j)次车最远到哪里,这显然可以倍增搞
然后考虑答案怎么算
对于询问((x,y)),求出(z=lca(x,y)),(x,y)先分别跳到距(z)最近的点(也就是下次就到(z)或更远),这时候先统计个答案步数(ans)
然后发现答案只有两种情况
Case#1
两点分别跳一次到(z),最终(ans=ans+2)
Case#2
设这时候(x,y)分别跳到了(x',y')
有一班车覆盖了路径((x',y')),那么答案就是(ans=ans+1),因为你只要坐这班车就可以越过LCA到另一个点
考虑怎么判断有没有一班车覆盖这条路径,转化一下变成是否有一班车((st,ed)),(st)在(x')子树中,(ed)在(y')子树中(包括(x'.y'))
如果你看过https://rye-catcher.github.io/2018/10/17/JZOI100019-A-dfs%E5%BA%8F-%E6%89%AB%E6%8F%8F%E7%BA%BF/
就会发现这还可以继续转化成(dfn[x']<=dfn[st]<=ed[x'],dfn[y']<=dfn[ed]<=ed[y'])
将((dfn[st],dfn[ed]))看成一个坐标,发现就是判断一个矩形中有没有点
似乎可以在线主席树做,也好像可以二分套二分,这里学到了一个新操作树状数组+扫描线+二维前缀和
我们转化后询问((x',y'))矩形的四个坐标为((dfn[x'],dfn[y']),(dfn[x'],ed[y']),(ed[x'],dfn[y']),(ed[x'],ed[y']))
一条班车路径转化成一个点((dfn[st],dfn[ed]))
我们把这些点放在一起按照扫描线思路,将点按横坐标进行排序,然后遍历所有点(优先遍历班车路径转化后的点)
如果是班车路径的点,加入树状数组([1,dfn[ed]])((dfn[ed])其实就是坐标(x,y)中的(y))前缀和
如果是个矩形想要查询里面点数咋办?二维前缀和.
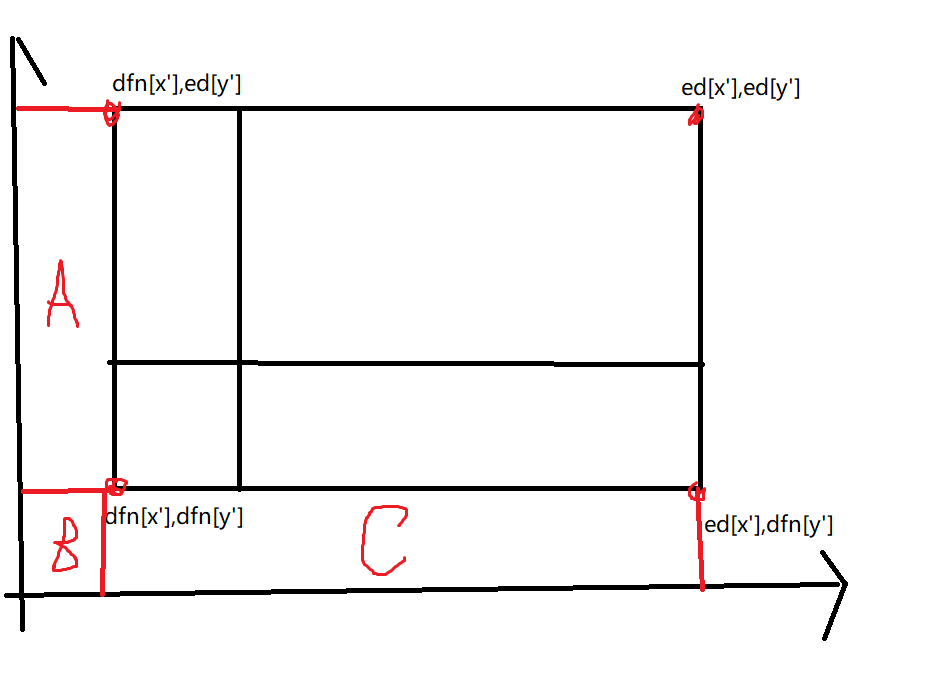
我们是将所有点按横坐标排序的,所以我们可以先加上(B)的点数,减去(A+B)的点数,然后等到(ed[x'])坐标时减去(B+C) 点数,最后加上整个大面积就是矩形内点数
显然这些部分直接查询树状数组前缀和就好了
然后有非常多的细节,见代码注释吧...
对于树上路径,我们都默认dfs序小的为起点方便处理,也算是个技巧
/*
code by RyeCatcher
*/
inline char gc(){
static char buf[SIZE],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,SIZE,stdin),p1==p2)?EOF:*p1++;
}
template <class T>inline void read(T &x){
x=0;int ne=0;char c;
while((c=gc())>'9'||c<'0')ne=c=='-';x=c-48;
while((c=gc())>='0'&&c<='9')x=(x<<3)+(x<<1)+c-48;x=ne?-x:x;return ;
}
const int maxn=500005;
const int inf=0x7fffffff;
int n,m,q;
struct Edge{
int ne,to;
}edge[maxn<<1];
int h[maxn],num_edge=1;
inline void add_edge(int f,int to){
edge[++num_edge].ne=h[f];
edge[num_edge].to=to;
h[f]=num_edge;
}
int f[maxn][23];
int dep[maxn],fa[maxn],son[maxn],size[maxn],top[maxn],dfn[maxn],ed[maxn],tot=0;
void dfs_1(int now){
int v;size[now]=1;
//if(now==150000)printf("wtf %d
",now,fa[now]);
for(ri i=h[now];i;i=edge[i].ne){
v=edge[i].to;
if(v==fa[now])continue;
dep[v]=dep[now]+1,fa[v]=now;
dfs_1(v);
size[now]+=size[v];
if(!son[now]||size[v]>size[son[now]])son[now]=v;
}
return ;
}
void dfs_2(int now,int t){
int v;
dfn[now]=++tot,top[now]=t;
if(!son[now]){
ed[now]=tot;
return ;
}
dfs_2(son[now],t);
for(ri i=h[now];i;i=edge[i].ne){
v=edge[i].to;
if(v==fa[now]||v==son[now])continue;
dfs_2(v,v);
}
ed[now]=tot;
return ;
}
inline int get_lca(int x,int y){
int xx=x,yy=y;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])std::swap(x,y);
x=fa[top[x]];
}
//if(!x)printf("--%d %d %d--
",xx,yy,x);
if(dep[x]>dep[y])return y;
return x;
}
void pre_dfs(int now){
int v;
for(ri i=h[now];i;i=edge[i].ne){
v=edge[i].to;
if(v==fa[now])continue;
pre_dfs(v);
if(!f[now][0]||(f[v][0]&&dep[f[now][0]]>dep[f[v][0]]))f[now][0]=f[v][0];//特判
}
return ;
}
struct Seg{
int x,y,id,d;
bool operator <(const Seg &rhs)const{
return (x==rhs.x)?id<rhs.id:x<rhs.x;
}
}seg[maxn<<2];
int sum[maxn<<2];
inline void update(int x,int k){for(;x<=n;x+=x&(-x))sum[x]+=k;}
inline int query(int x){
int tmp=0;
for(;x>=1;x-=x&(-x))tmp+=sum[x];
return tmp;
}
int fac[maxn],ans[maxn];
int qwq=0,pt[maxn];
int main(){
int x,y,lca;
//DEBUG
read(n);
fa[1]=0;
f[1][0]=1;
for(ri i=2;i<=n;i++){
f[i][0]=i;
read(fa[i]);
add_edge(i,fa[i]),add_edge(fa[i],i);
}
dep[1]=0;
dfs_1(1);
dfs_2(1,1);
read(m);
for(ri i=1;i<=m;i++){
read(x),read(y);
if(dfn[x]>dfn[y])std::swap(x,y);
lca=get_lca(x,y);
if(!f[x][0]||dep[f[x][0]]>dep[lca])f[x][0]=lca;
if(!f[y][0]||dep[f[y][0]]>dep[lca])f[y][0]=lca;
seg[++qwq]=(Seg){dfn[x],dfn[y],0,1};
}
pre_dfs(1);
fac[0]=1;
for(ri i=1;i<=n;i++)if(f[i][0]==i){
f[i][0]=0;//注意这里要置为不可行
}
for(ri k=1;k<=21;k++){
fac[k]=(fac[k-1]<<1);
for(ri i=1;i<=n;i++)f[i][k]=f[f[i][k-1]][k-1];
}
//for(ri k=0;k<=2;k++)for(ri i=1;i<=n;i++)printf("%d %d %d
",i,k,f[i][k]);
int po,qo;
read(q);
for(ri o=1;o<=q;o++){
read(x),read(y);
if(dfn[x]>dfn[y])std::swap(x,y);
lca=get_lca(x,y);
po=x,qo=y;
for(ri i=21;i>=0;i--)
if(dep[f[po][i]]>dep[lca]){
po=f[po][i];
ans[o]+=fac[i];
}
for(ri i=21;i>=0;i--)
if(dep[f[qo][i]]>dep[lca]){
qo=f[qo][i];
ans[o]+=fac[i];
}
if((!f[po][0]&&po!=lca)||(!f[qo][0]&&qo!=lca)){//注意!!
ans[o]=-1;
}
else {
if(po==lca||qo==lca){
ans[o]++;
//printf("--%d %d--
",o,ans[o]);
}
else {
ans[o]+=2;
//printf("--%d %d--
",o,ans[o]);
seg[++qwq]=(Seg){dfn[po]-1,dfn[qo]-1,o,1};//二维前缀和
seg[++qwq]=(Seg){ed[po],ed[qo],o,1};
seg[++qwq]=(Seg){dfn[po]-1,ed[qo],o,-1};
seg[++qwq]=(Seg){ed[po],dfn[qo]-1,o,-1};
}
}
}
std::sort(seg+1,seg+1+qwq);
for(ri i=1;i<=qwq;i++){
if(!seg[i].id){
update(seg[i].y,seg[i].d);
}
else{
pt[seg[i].id]+=seg[i].d*query(seg[i].y);
}
}
for(ri i=1;i<=q;i++){
if(pt[i])printf("%d
",ans[i]-1);
else printf("%d
",ans[i]);
}
return 0;
}