
代码:
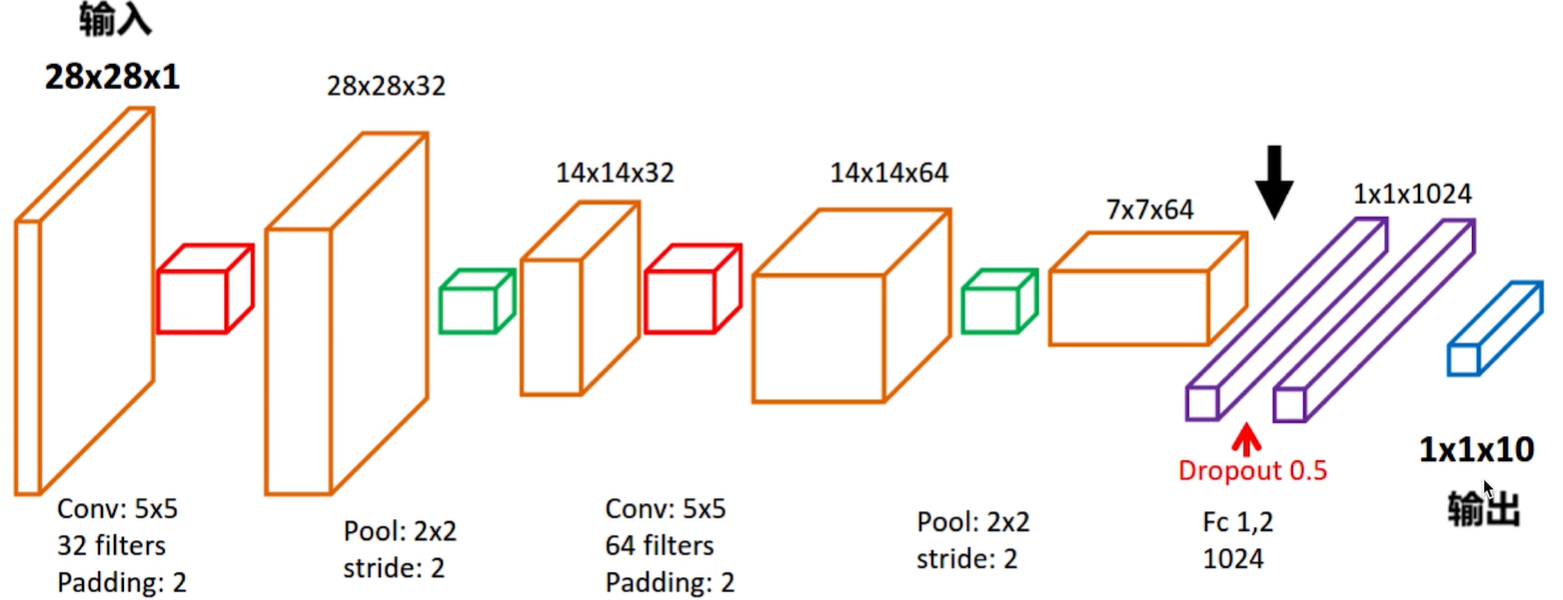
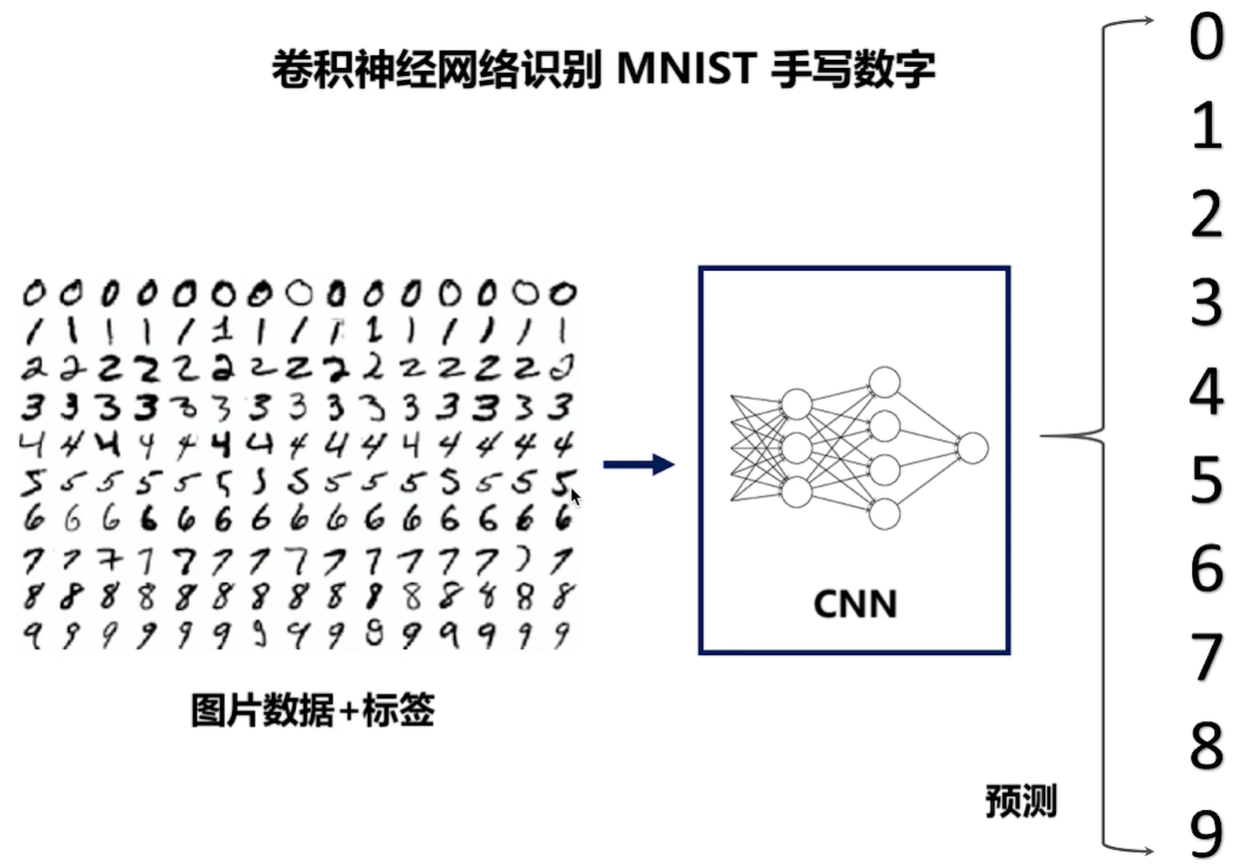
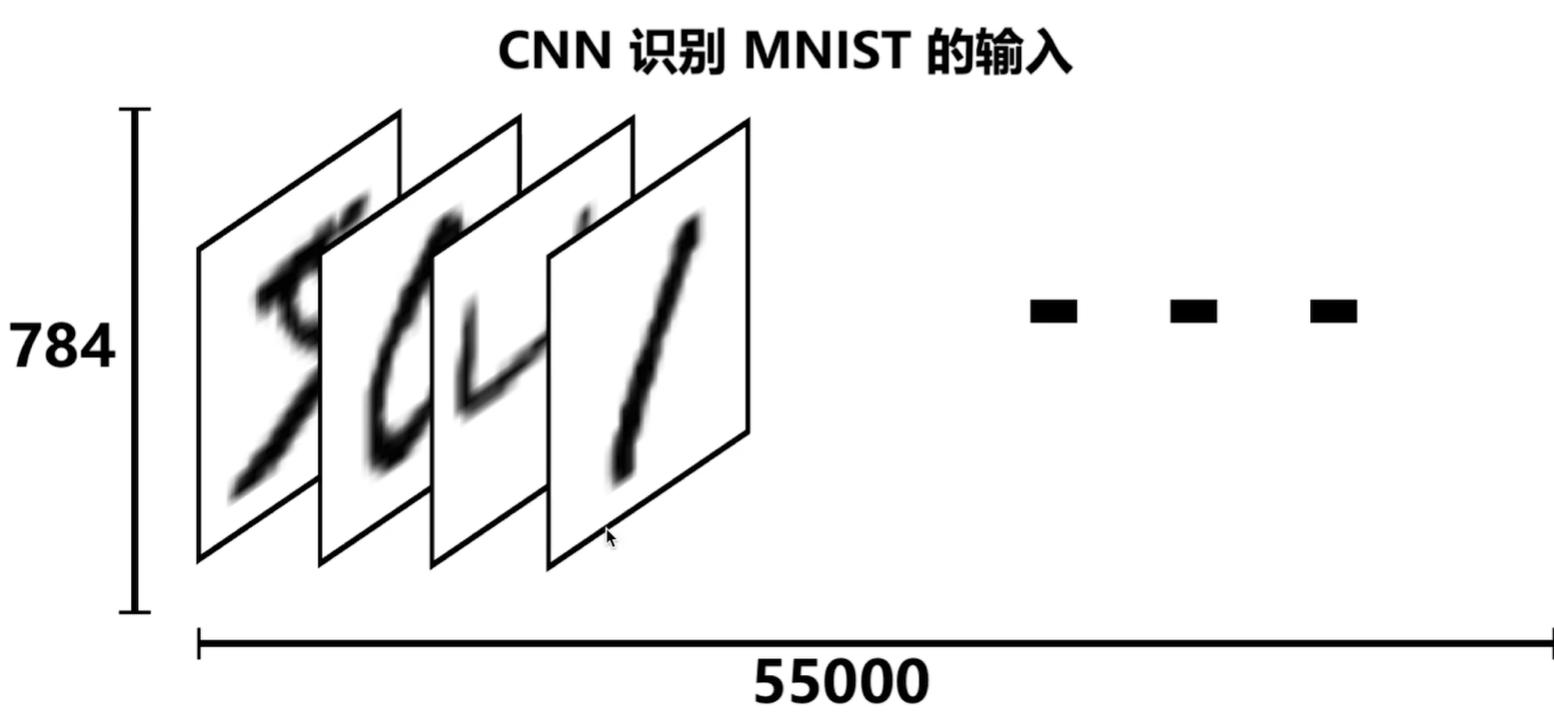
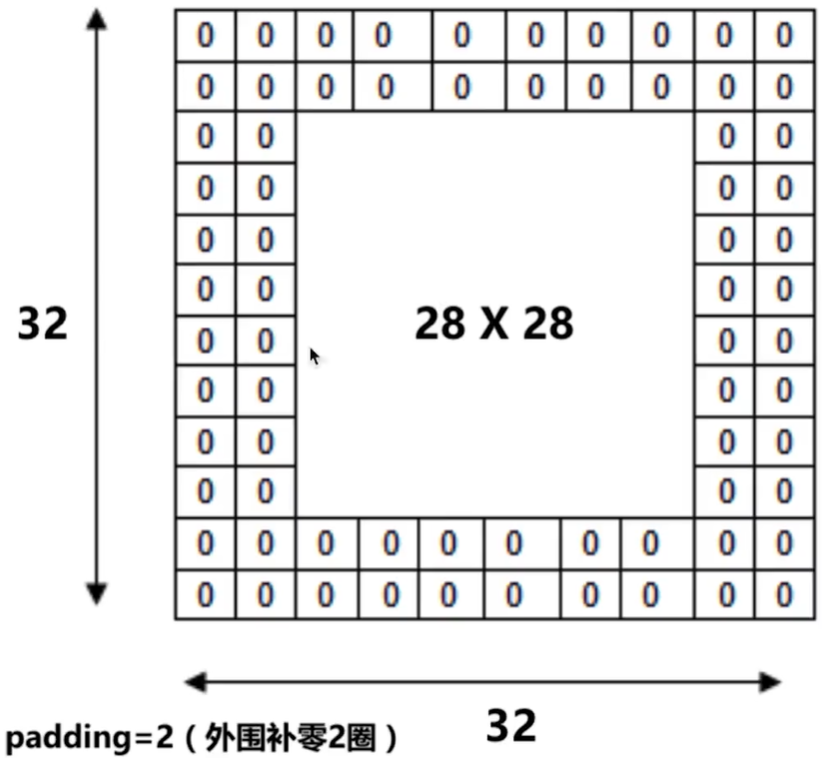
# -*- coding: UTF-8 -*- import numpy as np import tensorflow as tf # 下载并载入 MNIST 手写数字库(55000 * 28 * 28)55000 张训练图像 from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets('mnist_data', one_hot=True) # one_hot 独热码的编码(encoding)形式 # 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 的十位数字 # 0 : 1000000000 # 1 : 0100000000 # 2 : 0010000000 # 3 : 0001000000 # 4 : 0000100000 # 5 : 0000010000 # 6 : 0000001000 # 7 : 0000000100 # 8 : 0000000010 # 9 : 0000000001 # None 表示张量(Tensor)的第一个维度可以是任何长度 # 除以 255 是为了做 归一化(Normalization),把灰度值从 [0, 255] 变成 [0, 1] 区间 # 归一话可以让之后的优化器(optimizer)更快更好地找到误差最小值 input_x = tf.placeholder(tf.float32, [None, 28 * 28]) / 255. # 输入 output_y = tf.placeholder(tf.int32, [None, 10]) # 输出:10个数字的标签 # -1 表示自动推导维度大小。让计算机根据其他维度的值 # 和总的元素大小来推导出 -1 的地方的维度应该是多少 input_x_images = tf.reshape(input_x, [-1, 28, 28, 1]) # 改变形状之后的输入 # 从 Test(测试)数据集里选取 3000 个手写数字的图片和对应标签 test_x = mnist.test.images[:3000] # 图片 test_y = mnist.test.labels[:3000] # 标签 # 构建我们的卷积神经网络: # 第 1 层卷积 conv1 = tf.layers.conv2d( inputs=input_x_images, # 形状 [28, 28, 1] filters=32, # 32 个过滤器,输出的深度(depth)是32 kernel_size=[5, 5], # 过滤器在二维的大小是 (5 * 5) strides=1, # 步长是 1 padding='same', # same 表示输出的大小不变,因此需要在外围补零 2 圈 activation=tf.nn.relu # 激活函数是 Relu ) # 形状 [28, 28, 32] # 第 1 层池化(亚采样) pool1 = tf.layers.max_pooling2d( inputs=conv1, # 形状 [28, 28, 32] pool_size=[2, 2], # 过滤器在二维的大小是(2 * 2) strides=2 # 步长是 2 ) # 形状 [14, 14, 32] # 第 2 层卷积 conv2 = tf.layers.conv2d( inputs=pool1, # 形状 [14, 14, 32] filters=64, # 64 个过滤器,输出的深度(depth)是64 kernel_size=[5, 5], # 过滤器在二维的大小是 (5 * 5) strides=1, # 步长是 1 padding='same', # same 表示输出的大小不变,因此需要在外围补零 2 圈 activation=tf.nn.relu # 激活函数是 Relu ) # 形状 [14, 14, 64] # 第 2 层池化(亚采样) pool2 = tf.layers.max_pooling2d( inputs=conv2, # 形状 [14, 14, 64] pool_size=[2, 2], # 过滤器在二维的大小是(2 * 2) strides=2 # 步长是 2 ) # 形状 [7, 7, 64] # 平坦化(flat)。降维 flat = tf.reshape(pool2, [-1, 7 * 7 * 64]) # 形状 [7 * 7 * 64, ] # 1024 个神经元的全连接层 dense = tf.layers.dense(inputs=flat, units=1024, activation=tf.nn.relu) # Dropout : 丢弃 50%(rate=0.5) dropout = tf.layers.dropout(inputs=dense, rate=0.5) # 10 个神经元的全连接层,这里不用激活函数来做非线性化了 logits = tf.layers.dense(inputs=dropout, units=10) # 输出。形状 [1, 1, 10] # 计算误差(先用 Softmax 计算百分比概率, # 再用 Cross entropy(交叉熵)来计算百分比概率和对应的独热码之间的误差) loss = tf.losses.softmax_cross_entropy(onehot_labels=output_y, logits=logits) # Adam 优化器来最小化误差,学习率 0.001 train_op = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss) # 精度。计算 预测值 和 实际标签 的匹配程度 # 返回 (accuracy, update_op), 会创建两个 局部变量 accuracy = tf.metrics.accuracy( labels=tf.argmax(output_y, axis=1), predictions=tf.argmax(logits, axis=1),)[1] # 创建会话 sess = tf.Session() # 初始化变量:全局和局部 init = tf.group(tf.global_variables_initializer(), tf.local_variables_initializer()) sess.run(init) # 训练 5000 步。这个步数可以调节 for i in range(5000): batch = mnist.train.next_batch(50) # 从 Train(训练)数据集里取 “下一个” 50 个样本 train_loss, train_op_ = sess.run([loss, train_op], {input_x: batch[0], output_y: batch[1]}) if i % 100 == 0: test_accuracy = sess.run(accuracy, {input_x: test_x, output_y: test_y}) print("第 {} 步的 训练损失={:.4f}, 测试精度={:.2f}".format(i, train_loss, test_accuracy)) # 测试:打印 20 个预测值 和 真实值 test_output = sess.run(logits, {input_x: test_x[:20]}) inferred_y = np.argmax(test_output, 1) print(inferred_y, '推测的数字') # 推测的数字 print(np.argmax(test_y[:20], 1), '真实的数字') # 真实的数字 # 关闭会话 sess.close()
运行结果:
2020-02-20 17:20:50.016727: W tensorflow/core/framework/allocator.cc:113] Allocation of 301056000 exceeds 10% of system memory. 第 0 步的 训练损失=2.2992, 测试精度=0.40 2020-02-20 17:20:59.306664: W tensorflow/core/framework/allocator.cc:113] Allocation of 301056000 exceeds 10% of system memory. 第 100 步的 训练损失=0.0418, 测试精度=0.67 2020-02-20 17:21:08.120634: W tensorflow/core/framework/allocator.cc:113] Allocation of 301056000 exceeds 10% of system memory. 第 200 步的 训练损失=0.0204, 测试精度=0.77 2020-02-20 17:21:16.603976: W tensorflow/core/framework/allocator.cc:113] Allocation of 301056000 exceeds 10% of system memory. 第 300 步的 训练损失=0.0238, 测试精度=0.82 2020-02-20 17:21:26.259857: W tensorflow/core/framework/allocator.cc:113] Allocation of 301056000 exceeds 10% of system memory. 第 400 步的 训练损失=0.0067, 测试精度=0.85 第 500 步的 训练损失=0.1079, 测试精度=0.87 第 600 步的 训练损失=0.1508, 测试精度=0.89 第 700 步的 训练损失=0.0141, 测试精度=0.90 第 800 步的 训练损失=0.1056, 测试精度=0.91 第 900 步的 训练损失=0.0509, 测试精度=0.92 第 1000 步的 训练损失=0.0664, 测试精度=0.92 第 1100 步的 训练损失=0.0334, 测试精度=0.93 第 1200 步的 训练损失=0.0108, 测试精度=0.93 第 1300 步的 训练损失=0.0019, 测试精度=0.93 第 1400 步的 训练损失=0.0092, 测试精度=0.94 第 1500 步的 训练损失=0.0060, 测试精度=0.94 第 1600 步的 训练损失=0.0285, 测试精度=0.94 第 1700 步的 训练损失=0.0379, 测试精度=0.94 第 1800 步的 训练损失=0.0366, 测试精度=0.95 第 1900 步的 训练损失=0.0305, 测试精度=0.95 第 2000 步的 训练损失=0.0043, 测试精度=0.95 第 2100 步的 训练损失=0.0401, 测试精度=0.95 第 2200 步的 训练损失=0.0104, 测试精度=0.95 第 2300 步的 训练损失=0.0042, 测试精度=0.95 第 2400 步的 训练损失=0.0084, 测试精度=0.95 第 2500 步的 训练损失=0.0147, 测试精度=0.96 第 2600 步的 训练损失=0.0010, 测试精度=0.96 第 2700 步的 训练损失=0.0012, 测试精度=0.96 第 2800 步的 训练损失=0.0415, 测试精度=0.96 第 2900 步的 训练损失=0.0090, 测试精度=0.96 第 3000 步的 训练损失=0.0418, 测试精度=0.96 第 3100 步的 训练损失=0.0379, 测试精度=0.96 第 3200 步的 训练损失=0.0003, 测试精度=0.96 第 3300 步的 训练损失=0.0090, 测试精度=0.96 第 3400 步的 训练损失=0.0008, 测试精度=0.96 第 3500 步的 训练损失=0.0037, 测试精度=0.96 第 3600 步的 训练损失=0.0157, 测试精度=0.96 第 3700 步的 训练损失=0.0019, 测试精度=0.97 第 3800 步的 训练损失=0.0123, 测试精度=0.97 第 3900 步的 训练损失=0.0048, 测试精度=0.97 第 4000 步的 训练损失=0.0069, 测试精度=0.97 第 4100 步的 训练损失=0.0212, 测试精度=0.97 第 4200 步的 训练损失=0.0025, 测试精度=0.97 第 4300 步的 训练损失=0.0087, 测试精度=0.97 第 4400 步的 训练损失=0.0039, 测试精度=0.97 第 4500 步的 训练损失=0.0126, 测试精度=0.97 第 4600 步的 训练损失=0.0019, 测试精度=0.97 第 4700 步的 训练损失=0.0037, 测试精度=0.97 第 4800 步的 训练损失=0.0013, 测试精度=0.97 第 4900 步的 训练损失=0.0020, 测试精度=0.97 [7 2 1 0 4 1 4 9 5 9 0 6 9 0 1 5 9 7 3 4] 推测的数字 [7 2 1 0 4 1 4 9 5 9 0 6 9 0 1 5 9 7 3 4] 真实的数字