之前我们涉及过线性回归，不过那个是单元的（一个未知数X），这回我们来学习一下多元线性回归（多个X）。
首先我们给一组房子数据：
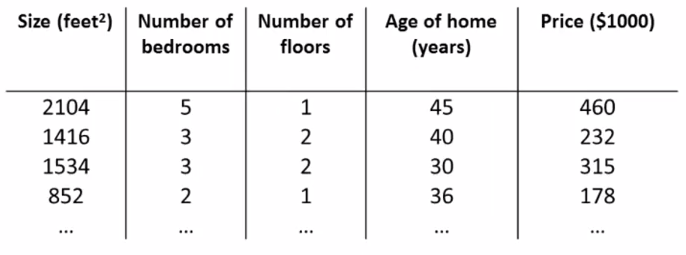
我们给出几个关于多元线性回归的概念（我们把价格设为y，其他设为x）：
- n ： 特征数量（这里就是4）
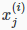：第i组特征里的第j个特征
：第i组特征
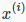可以用向量的方式表示。比如x(2) = 
多元线性回归方程就为：
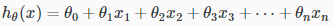
还可以写成：
hθ(x)=θ0x0+θ1x1+θ2x2+θ3x3+⋯+θnxn (x0 = 1)
然后我们可以用矩阵来表示这个多元线性回归函数。（矩阵的知识请看我之前的文章）
用矩阵方式写成：
化简一下为：
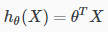
接下来我们讨论一下多元线性回归的梯度下降
我们已经了解过单元线性归回的梯度下降。而多元可以理解成对多个特征x进行梯度下降。
所以我们需要重复以下函数直到收敛
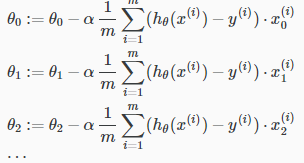
或者说可以写成这样:
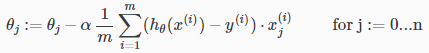
这个公式和之前的梯度下降函数差在了哪里
其实就是多乘了一个x特性。
怎么使梯度下降更好的工作
特征收缩
确保不同特征的取值，在相近的范围内，这样梯度下降就能更好的收敛。
可以将特征值约束到-3到3内
比如说：
有一个房子面积特征x1，取值为0~2000，有一个房间数x2，取值为0~5.
x1 / 2000
x2 / 5
来保证让x1的取值为0~1，x2的取值为0~1.
均值归一化
特征收缩的另一个方法。如果你有特征xi，用xi-ui / si来替换xi，使其具有0的平均值（不用替换x0，因为x0衡为1）
xi = (xi - ui) / si
ui：训练集中xi的平均值
si：该特征值的范围（最大减最小）