B. Irreducible Anagrams【CF 1290B】

思路：

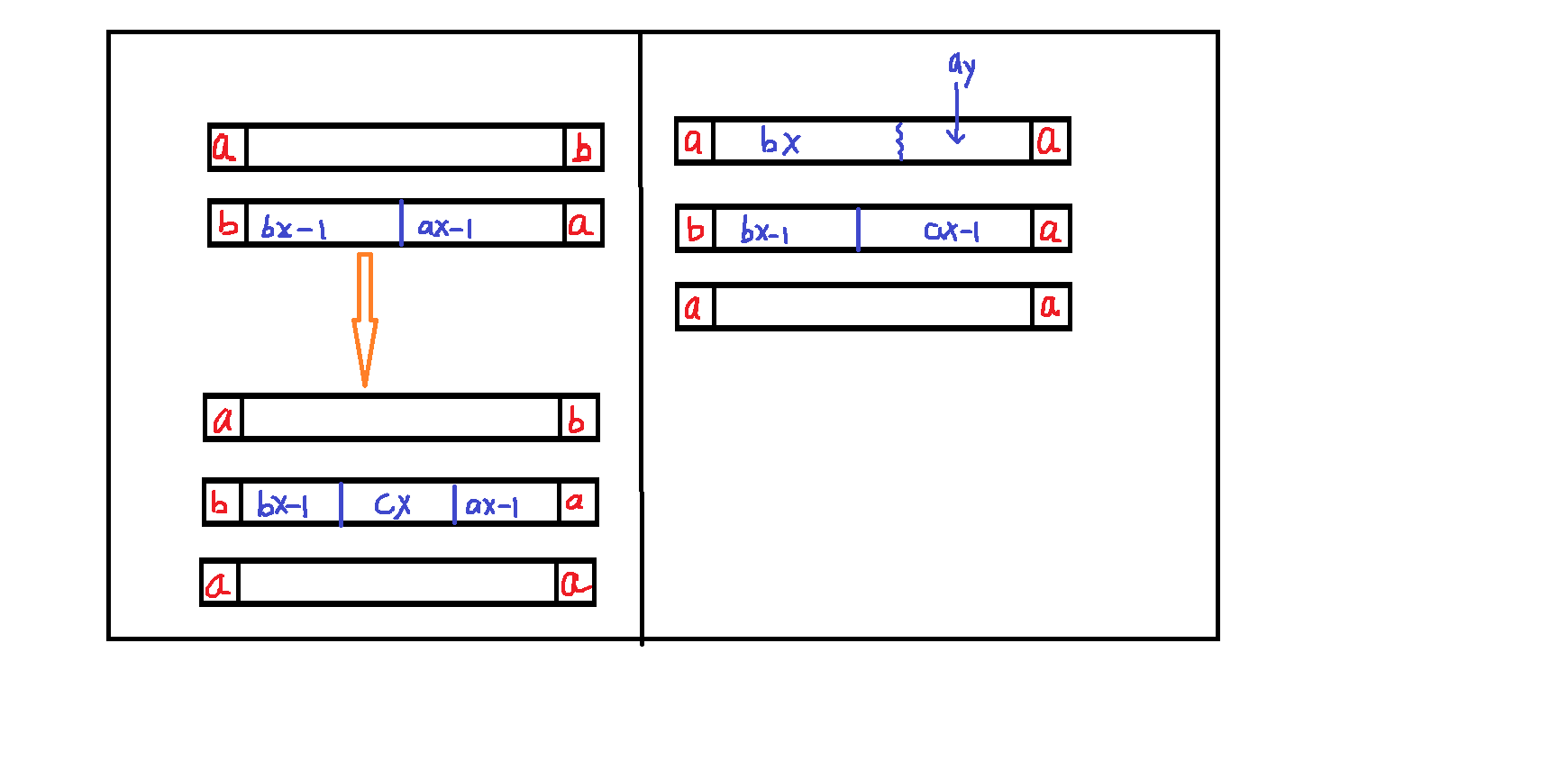
设tx为t类别字符的个数。

①对于长度小于2的t明显是"YES"
②对于字符类别只有1个的t明显是"YES"
③对于字符类别有2个的t，如左上图：如果str[l] != str[r],那么我们构造的t也应该是str[l] != str[r]，且s字串和t的str[l]和str[r]是相反的，即如图所示。继续，如图构造，即bbb..a...a这样，我们发现第一个图片除去str[l] = a和str[r]=b之外，中间怎么放置字符，都会出现"Irreducible Anagrams"的情况，所以"YES"。
④对于字符类别有2个的t，如果str[l] == str[r]，如右边的图，总有k = 2，让s1包含一个a和bx个b,s2包含剩余的ay个a使得满足"reducible Anagrams",所以"NO"。
④对于字符类别有3个的t，按着左上的图也无法构造出"Irreducible Anagrams" 情况，说明字符类别为3的t，说明不论字符排列都存在"reducible Anagrams",所以"NO"。
⑤对于字符类别大于3个的t，由④推出是"NO"。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 2e5 + 10;
int dp[30][N];
char str[N];

void solve()
{
    scanf("%s", str);
    int n = strlen(str);

    for(int i = 1; i <= n; ++i) {
        dp[str[i - 1] - 'a'][i]++;
        for(int c = 0; c < 26; ++c) {
            dp[c][i] += dp[c][i - 1];
        }
    }
/*
    for(int c = 0; c < 26; ++c) {
        printf("%c :
", 'a' + c);
        for(int i = 1; i <= n; ++i) {
            printf("%d ", dp[c][i]);
        }
        printf("
");
    }
*/
    int q;
    scanf("%d", &q);
    vector<pair<int ,int > > vp;
    for(int i = 0; i < q; ++i) {
        int l, r;
        scanf("%d%d", &l, &r);
        vp.push_back(make_pair(l, r));
    }

    ///vector<int > ans;
    for(auto info : vp) {
        int l = info.first;
        int r = info.second;

        int kinds = 0;
        int sum = 0;
        for(int c = 0; c < 26; ++c) {
            kinds += (dp[c][r] - dp[c][l - 1]) > 0;
            sum += dp[c][r] - dp[c][l - 1];
        }
        ///cout << "tot = " << kinds << endl;
        if(sum == 1 || (kinds == 2 && str[l - 1] != str[r - 1]) || kinds > 2) {
            printf("YES
");
        } else printf("NO
");
    }

}

int main()
{
    solve();

    return 0;
}