先写出朴素的DP方程f[i][j]=f[k][j-1]+h[k+1][i] {k<i}(h表示[k+1,j]有几个不同的数)
显然时间空间复杂度都无法承受
仔细想想可以发现对于一个点 i 从 k 转移了,证明了 1~k 中 k 一定是最优的,不论对于i或者i之后的任何点x都是如此,不存在对i最优但对i之后的任何点x更优,否则i也可以更优(因为只多了一段h[i+1][x](i<x),而这一段显然是相同的),其实打表也能看出来(orz CYC!)
证明:
假设a<b,k>l,a从k转移最优,b从l转移最优
则有
f[k]+h[k+1][b]<f[l]+h[l+1][b],f[l]+h[l+1][a]<f[k]+h[k+1][a]
则有
h[k+1][b]+h[l+1][a]<h[l+1][b]+h[k+1][a]
则有
h[k+1][b]-h[k+1][a]<h[l+1][b]-h[l+1][a]
则有
h[a][b]<h[a][b]
∴不成立
于是我们就证明了这题的决策单调性
有了这个性质之后我们就可以分治优化了,查询一个区间里有多少个不同的数用主席树就行了。
效率O(KNlogNlogN)约等于4亿...TLE QAQ
实际上主席树有更巧妙的用法可以优化到KNlogN,等会补 不会,委屈的折耳猫.jpg
在CYC大爷的教导下会了!本来不保证复杂度的话直接边分治边递推就行了,但是R~MID可能被统计多次,会TLE。那怎么办呢,把这一段用主席树查一下,就可以把复杂度降低到log了。这样的log是独立于转移之外的,复杂度为O(NKlogN)
而且常数明显是比线段树小的!线段树需要区间修改,上传下传,而且每次转移完都要修改,而主席树建树之后就不用再修改了,并且建树是O(NlogN)的,跑的飞快。
以下全部为极限数据(未打开O2优化):
主席树:

线段树:
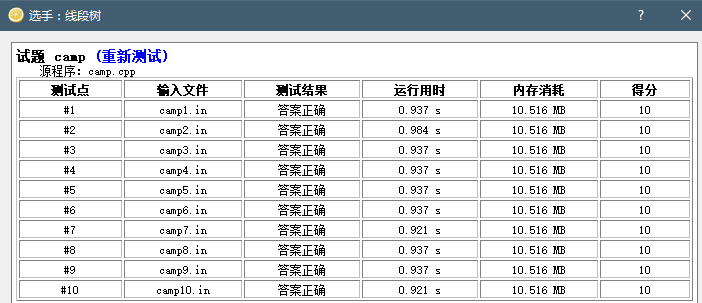
代码已更新

#include<iostream> #include<cstdlib> #include<cstring> #include<cstdio> #include<algorithm> #include<queue> #include<cmath> #include<map> #define ll long long using namespace std; const int maxn=50010,inf=1e9; struct poi{int sum,lt,rt;}tree[maxn*20]; int n,K,N,now,sz; int a[maxn],b[maxn],f[maxn][2],root[maxn],pre[maxn],last[maxn],h[maxn],next[maxn]; bool v[maxn]; void read(int &k) { int f=1;k=0;char c=getchar(); while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar(); while(c<='9'&&c>='0')k=k*10+c-'0',c=getchar(); k*=f; } inline void update(int &x,int l,int r,int cx) { tree[++sz]=tree[x];tree[sz].sum++;x=sz; if(l==r)return; int mid=(l+r)>>1; if(cx<=mid)update(tree[x].lt,l,mid,cx); else update(tree[x].rt,mid+1,r,cx); } inline int query(int x,int y,int l,int r,int cl,int cr) { if(cl<=l&&r<=cr)return tree[y].sum-tree[x].sum; int mid=(l+r)>>1,ret=0; if(cl<=mid)ret+=query(tree[x].lt,tree[y].lt,l,mid,cl,cr); if(cr>mid)ret+=query(tree[x].rt,tree[y].rt,mid+1,r,cl,cr); return ret; } void solve(int l,int r,int L,int R,int now) { if(l>r||L>R)return; int mid=(l+r)>>1; int pos;f[mid][now&1]=-inf; int noww=0; if(R+1<mid)noww=query(root[R+1],root[mid],0,n,0,R+1); for(int i=min(R+1,mid);i>L;i--) { if(next[i]>mid)noww++; h[i]=noww; } for(int i=L;i<=R&&i<mid;i++) { if(f[i][(now&1)^1]+h[i+1]>f[mid][now&1]) f[mid][now&1]=f[i][(now&1)^1]+h[i+1],pos=i; } solve(l,mid-1,L,pos,now);solve(mid+1,r,pos,R,now); } int main() { freopen("camp.in","r",stdin); freopen("camp.out","w",stdout); read(n);read(K); for(int i=1;i<=n;i++)read(a[i]),b[i]=a[i];N=n; sort(b+1,b+1+N);N=unique(b+1,b+1+N)-b-1; for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+1+N,a[i])-b; for(int i=1;i<=n;i++)pre[i]=last[a[i]],last[a[i]]=i; memset(last,32,(n+1)<<2); for(int i=n;i;i--)next[i]=last[a[i]],last[a[i]]=i; for(int i=1;i<=n;i++)update(root[i]=root[i-1],0,n,pre[i]); for(int i=1;i<=K;i++)solve(1,n,0,n,i); printf("%d ",f[n][K&1]); return 0; }
那个方程还可以直接用线段树优化,同样是记录上次出现的位置,加入一个数有影响的只有上次出现位置+1开始的区间,然后就线段树存一下转移方程右边的值logn找max就行了

#include<iostream> #include<cstring> #include<cstdlib> #include<cstdio> #include<cmath> #include<algorithm> using namespace std; const int maxn=40010,inf=1e9; struct poi{int max,delta;}tree[maxn*10]; int n,K,N,cnt; int a[maxn],b[maxn],pre[maxn],root; int f[maxn][51]; void read(int &k) { int f=1;k=0;char c=getchar(); while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar(); while(c<='9'&&c>='0')k=k*10+c-'0',c=getchar(); k*=f; } inline int max(int a,int b){return a>b?a:b;} inline void pushup(int x){tree[x].max=max(tree[x<<1].max,tree[x<<1|1].max);} inline void pushdown(int x) { if(!tree[x].delta)return; tree[x<<1].delta+=tree[x].delta; tree[x<<1|1].delta+=tree[x].delta; tree[x<<1].max+=tree[x].delta; tree[x<<1|1].max+=tree[x].delta; tree[x].delta=0; } void build(int x,int l,int r,int ty) { if(l==r){tree[x].max=f[l-1][ty];tree[x].delta=0;return;} int mid=(l+r)>>1;tree[x].delta=0; build(x<<1,l,mid,ty); build(x<<1|1,mid+1,r,ty); pushup(x); } inline void add(int x,int l,int r,int cl,int cr) { if(cl<=l&&r<=cr){tree[x].max++;tree[x].delta++;return;} pushdown(x); int mid=(l+r)>>1; if(cl<=mid)add(x<<1,l,mid,cl,cr); if(cr>mid)add(x<<1|1,mid+1,r,cl,cr); pushup(x); } inline int query(int x,int l,int r,int cl,int cr) { if(cl<=l&&r<=cr)return tree[x].max; pushdown(x); int mid=(l+r)>>1,ans=0; if(cl<=mid)ans=query(x<<1,l,mid,cl,cr); if(cr>mid)ans=max(ans,query(x<<1|1,mid+1,r,cl,cr)); return ans; } int main() { freopen("camp.in","r",stdin); freopen("camp.ans","w",stdout); read(n);read(K); for(int i=1;i<=n;i++)read(a[i]),b[i]=a[i];N=n; N=unique(b+1,b+1+N)-b-1;sort(b+1,b+1+N); for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+1+n,a[i])-b; for(int j=1;j<=K;j++) { for(int i=1;i<=n;i++) { add(1,1,n+1,pre[a[i]]+1,i); f[i][j]=query(1,1,n+1,1,i); pre[a[i]]=i; } if(j==K)continue; build(1,1,n+1,j);for(int i=1;i<=n;i++)pre[a[i]]=0; } printf("%d ",f[n][K]); }
makedata:

#include<iostream> #include<iostream> #include<cstring> #include<cstdlib> #include<cstdio> #include<ctime> using namespace std; int main() { freopen("camp10.in","w",stdout); srand(time(0)); int n=35000; printf("%d %d ",n,50); for(int i=1;i<=n;i++) printf("%d ",233333333+rand()%(1+rand()%10)); }
