bzoj4518: [Sdoi2016]征途（DP+决策单调性分治优化）

　　题目要求...

　　化简得...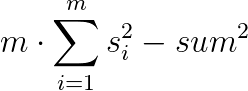

　　显然m和sum^2是已知的，那么只要让sigma(si^2)最小，那就变成了求最小平方和的最小值，经典的决策单调性，用分治优化即可。

　　斜率优化忘得差不多就不写了

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio> 
#include<algorithm>
#define ll long long 
using namespace std;
const int maxn=3010,inf=1e9;
int n,m,x,y,z,tot;
int a[maxn],sum;
int f[maxn][maxn];
void read(int &k)
{
    int f=1;k=0;char c=getchar();
    while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar();
    while(c<='9'&&c>='0')k=k*10+c-'0',c=getchar();
    k*=f;
}
void solve(int l,int r,int L,int R,int now)
{
    if(l>r||L>R)return;
    int mid=(l+r)>>1,value=inf,pos;
    for(int i=L;i<mid&&i<=R;i++)
    if((a[mid]-a[i])*(a[mid]-a[i])+f[i][now-1]<value)
    value=(a[mid]-a[i])*(a[mid]-a[i])+f[i][now-1],pos=i;
    f[mid][now]=value;
    solve(l,mid-1,L,pos,now);solve(mid+1,r,pos,R,now);
}
int main()
{
    read(n);read(m);
    for(int i=1;i<=n;i++)read(a[i]),sum+=a[i],a[i]+=a[i-1];
    for(int i=1;i<=n;i++)f[i][0]=inf;
    for(int j=1;j<=m;j++)
    solve(1,n,0,n,j);
    printf("%lld",1ll*m*f[n][m]-1ll*sum*sum);
    return 0;
}