早上打一半就回家了...
T1傻逼题不说了...而且我的写法比题解要傻逼很多T T
T2可以发现,我们强制最大值所在的块是以左上为边界的倒三角,然后旋转4次就可以遍历所有的情况。所以二分极差,把最大值所能扩展到的(mp[i][j]+mid>=mx)最大倒三角求出来,剩下的数减去最小值判断一下是否小于等于极差,如果是的话答案可行。

#include<iostream> #include<cstring> #include<cstdlib> #include<cstdio> #include<algorithm> #define ll long long using namespace std; const int maxn=2010,inf=1e9; int mn,mx; int n[4],m[4],mp[4][maxn][maxn]; bool v[maxn][maxn]; void read(int &k) { int f=1;k=0;char c=getchar(); while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar(); while(c<='9'&&c>='0')k=k*10+c-'0',c=getchar(); k*=f; } void rotate(int x,int y) { for(int i=1;i<=n[x];i++) for(int j=1;j<=m[x];j++) mp[y][j][n[x]-i+1]=mp[x][i][j]; n[y]=m[x];m[y]=n[x]; } bool check(int x,int mid) { memset(v,0,sizeof(v)); int now=m[x]; for(int i=1;i<=n[x];i++) for(int j=1;j<=now;j++) if(mp[x][i][j]+mid<mx){now=j-1;break;} else v[i][j]=1; for(int i=n[x];i;i--) for(int j=m[x];j;j--) if(v[i][j])break; else if(mp[x][i][j]-mid>mn)return 0; return 1; } int main() { read(n[0]);read(m[0]);mn=inf; for(int i=1;i<=n[0];i++)for(int j=1;j<=m[0];j++)read(mp[0][i][j]),mx=max(mx,mp[0][i][j]),mn=min(mn,mp[0][i][j]); rotate(0,1);rotate(1,2);rotate(2,3); int l=0,r=mx-mn; while(l<r) { int mid=(l+r)>>1; if(check(0,mid)||check(1,mid)||check(2,mid)||check(3,mid))r=mid; else l=mid+1; } printf("%d ",l); return 0; }
T3超喵的题啊,虽然标程好像出了点小偏差,已经跟管理员反馈了,但是现在暂时还没有更正,还是先水一篇博客要紧...
首先要知道扩展欧拉定理...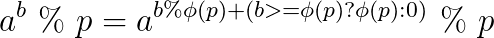
我们知道p<=2e7,所以可以先预处理出2e7内的phi(我写个埃式筛怎么比线性筛慢那么多T T)。因为一个数最多经过log次求phi的操作就会变成1,当变成1的时候后面的数就没有意义了,所以对于一个区间的询问,我们可以递归地计算指数,直到1就返回1,或者直到区间扫完就返回当前位置的值,效率O(logP)。但是我们怎么判断当前指数是否大于phi(p)呢,可以发现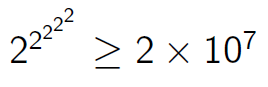 ,所以我们只要知道后5位的数就可以判断指数是否大于phi(p)了。然后一边递归一边快速幂,用BIT维护区间修改,单点查询,就可以了。
,所以我们只要知道后5位的数就可以判断指数是否大于phi(p)了。然后一边递归一边快速幂,用BIT维护区间修改,单点查询,就可以了。
这个代码现在只有90分,等管理员更正数据后就能AC了...
UPD:数据已更正,状态里瞬间只剩下我一个人AC...
UPD:改成线性筛快了好多...

#include<iostream> #include<cstring> #include<cstdlib> #include<cstdio> #include<algorithm> #define ll long long using namespace std; const int maxn=500010,inf=1e9,lim=2e7; int n,m,ty,x,y,z,cnt; int phi[20000010],v[maxn],prime[20000010]; ll tree[maxn],a[maxn]; bool vis[20000010]; void read(int &k) { int f=1;k=0;char c=getchar(); while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar(); while(c<='9'&&c>='0')k=k*10+c-'0',c=getchar(); k*=f; } inline int lowbit(int x){return x&-x;} inline void add(int x,int delta){for(;x<=n;x+=lowbit(x))tree[x]+=delta;}; inline ll querysum(int x){ll sum=0;for(;x;x-=lowbit(x))sum+=tree[x];return sum;} inline ll query(int x) { if(v[x]==m+1)return a[x]; v[x]=m+1;return a[x]=querysum(x); } inline int power(int a,int b,int mod) { if(!a)return 0;int ans=1; for(;b;b>>=1,a=1ll*a*a%mod) if(b&1)ans=1ll*ans*a%mod; return ans; } int solve(int l,int r,int mod) { if(mod==1)return 1; ll now=query(l)%mod;if(!now)return 0;if(l==r)return now; int nxt=min(l+5,r); for(int i=l+1;i<nxt;i++)if(query(i)==1){nxt=r=i;break;} ll last=query(nxt),x; if(last>=phi[mod])return power(now,solve(l+1,r,phi[mod])+phi[mod],mod); for(int i=nxt-1;i>l;i--) { ll mi=last;last=1;x=query(i); for(int j=1;j<=mi;j++) { last*=x; if(last>=phi[mod])return power(now,solve(l+1,r,phi[mod])+phi[mod],mod); } } return power(now,solve(l+1,r,phi[mod]),mod); } inline void getphi() { phi[1]=1; for(int i=2;i<=lim;i++) { if(!vis[i])prime[++cnt]=i,phi[i]=i-1; for(int j=1;j<=cnt;j++) { int t=i*prime[j];if(t>lim)break; vis[t]=1; if(i%prime[j]==0){phi[t]=phi[i]*prime[j];break;} phi[t]=phi[i]*(prime[j]-1); } } } int main() { getphi();read(n);read(m);int pre=0; for(int i=1;i<=n;i++)read(x),add(i,x-pre),pre=x; while(m--) { read(ty);read(x);read(y);read(z); if(ty==1)add(x,z),add(y+1,-z); else printf("%d ",solve(x,y,z)%z); } return 0; }
