这题好久之前就被学长安利了...一直没写珍藏在收藏夹一个不为人知的角落233
这题怎么做...我们来数形结合,横坐标为$t_i$被加的次数(可看作时间$t$),纵坐标为$v_i$,那么$t_i$实际上就是阶梯图形的面积。
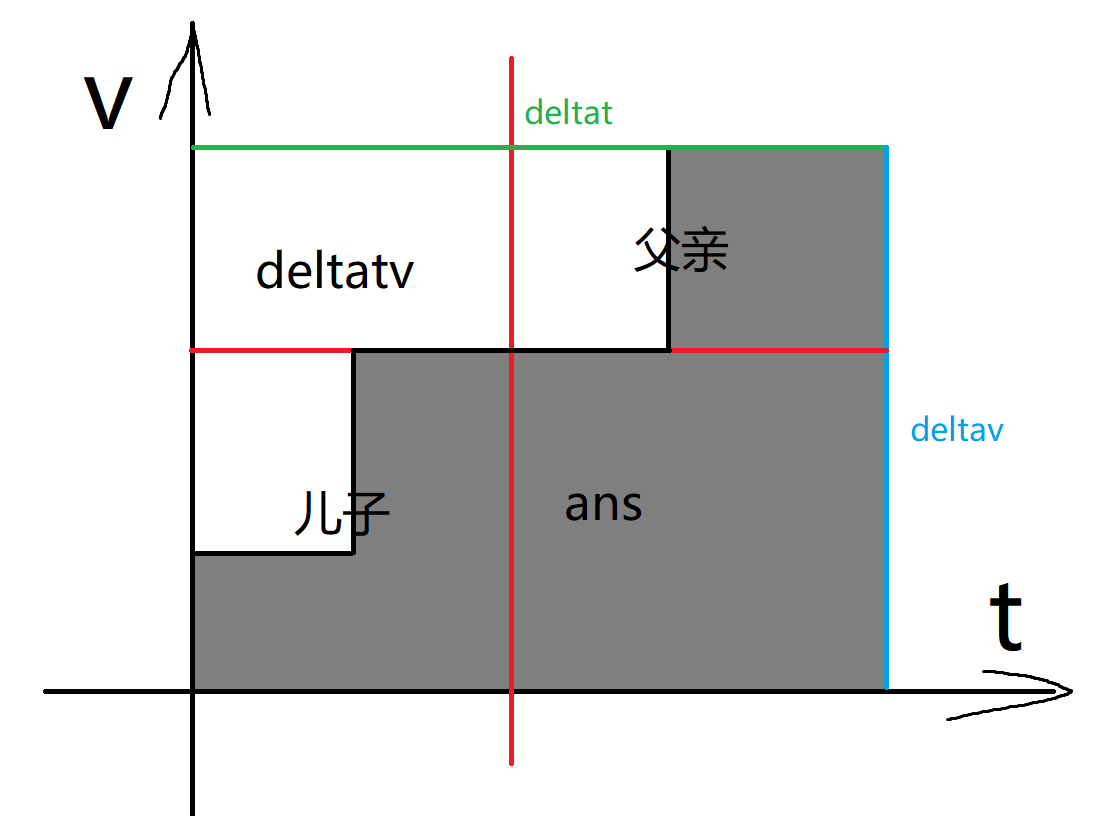
上图是父亲节点和子节点合并后的样子,阴影部分为答案即$t_i$,显然可以通过$deltat*deltav-deltatv$来得到。
信息下传的时候儿子的$deltatv$加上父亲的$deltatv$后还要加上一个长方体的面积即$deltat_{son}*deltav_{fa}$,然后儿子的$deltat$和$deltav$都加上父亲的就行了。

#include<iostream> #include<cstring> #include<cstdlib> #include<cstdio> #include<algorithm> #define ll long long using namespace std; const int maxn=200010, inf=1e9; struct poi{int too, pre;}e[maxn<<1]; struct tjm{ll deltat, deltav, deltatv;}tree[maxn<<2]; int n, m, tott, tot, ty, x, y, z; int fa[maxn], d[maxn], size[maxn], top[maxn], w[maxn], last[maxn], son[maxn]; char buf[8000000], *ptr=buf-1; inline void read(int &k) { int f=1; k=0; char c=*++ptr; while(c<'0' || c>'9') c=='-'&&(f=-1), c=*++ptr; while(c<='9' && c>='0') k=k*10+c-'0', c=*++ptr; k*=f; } inline void add(int x, int y){e[++tot]=(poi){y, last[x]}; last[x]=tot;} void dfs1(int x) { size[x]=1; for(int i=last[x], too;i;i=e[i].pre) { d[too=e[i].too]=d[x]+1; dfs1(too); size[x]+=size[too]; if(size[too]>size[son[x]]) son[x]=too; } } void dfs2(int x, int tp) { top[x]=tp; w[x]=++tott; if(son[x]) dfs2(son[x], tp); for(int i=last[x], too;i;i=e[i].pre) if((too=e[i].too)!=son[x]) dfs2(too, too); } inline void addone(int x, ll deltat, ll deltav, ll deltatv) { tree[x].deltatv+=deltatv+deltav*tree[x].deltat; tree[x].deltat+=deltat; tree[x].deltav+=deltav; } inline void down(int x) { addone(x<<1, tree[x].deltat, tree[x].deltav, tree[x].deltatv); addone(x<<1|1, tree[x].deltat, tree[x].deltav, tree[x].deltatv); tree[x].deltat=tree[x].deltav=tree[x].deltatv=0; } void update(int x, int l, int r, int cl, int cr, int delta, int ty) { if(cl<=l && r<=cr) { if(ty) tree[x].deltat+=delta; else tree[x].deltatv+=tree[x].deltat*delta, tree[x].deltav+=delta; return; } down(x); int mid=(l+r)>>1; if(cl<=mid) update(x<<1, l, mid, cl, cr, delta, ty); if(cr>mid) update(x<<1|1, mid+1, r, cl, cr, delta, ty); } ll query(int x, int l, int r, int cx) { if(l==r) return tree[x].deltat*tree[x].deltav-tree[x].deltatv; down(x); int mid=(l+r)>>1; if(cx<=mid) return query(x<<1, l, mid, cx); else return query(x<<1|1, mid+1, r, cx); } inline void solve(int x, int y, int delta, int ty) { int f1=top[x], f2=top[y]; while(f1!=f2) { if(d[f1]<d[f2]) swap(x, y), swap(f1, f2); update(1, 1, n, w[f1], w[x], delta, ty); x=fa[f1]; f1=top[x]; } if(d[x]<d[y]) swap(x, y); update(1, 1, n, w[y], w[x], delta, ty); } int main() { fread(buf, 1, sizeof(buf), stdin); read(n); for(int i=2;i<=n;i++) read(fa[i]), add(fa[i], i); dfs1(1); dfs2(1, 1); read(m); for(int i=1;i<=m;i++) read(ty), read(x), read(y), solve(1, x, y, ty-1); for(int i=1;i<=n;i++) printf("%lld ", query(1, 1, n, w[i])); }
如果这题要求区间和呢?因为一个区间内可能有很多个阶梯形,但是上传的时候都是接上同样的一段父亲的阶梯,所以这个贡献还是可以计算的,只需要多记录一下区间内的$sumv,sumt$就很好求了。
