【luogu P1879】Corn Fields G / 又是他Farmer John / 玉米田（加强版）（状压DP）（轮廓线DP）

Corn Fields G / 又是他Farmer John / 玉米田（加强版）

题目链接：luogu P1879

题目大意

给你一个 n*m 的矩阵，有一些位置可以选放不放东西。
然后规定一个东西旁边四个位置不能有东西。
问你有多少种放的方案。

思路

看到这个大小，我们考虑状压 DP。
不难列出 (2^{n+m}) 的式子，然后就能过 luogu 的。

但是 jzoj 的是加强版，就会 TLE。
我们考虑优化，写轮廓线 DP。
轮廓线 DP 大概就是你设 (f_{i,j,k}) 就是处理到 (i,j) 的位置，轮廓线状态是 (k) 的方案数。
处理到时什么意思呢？

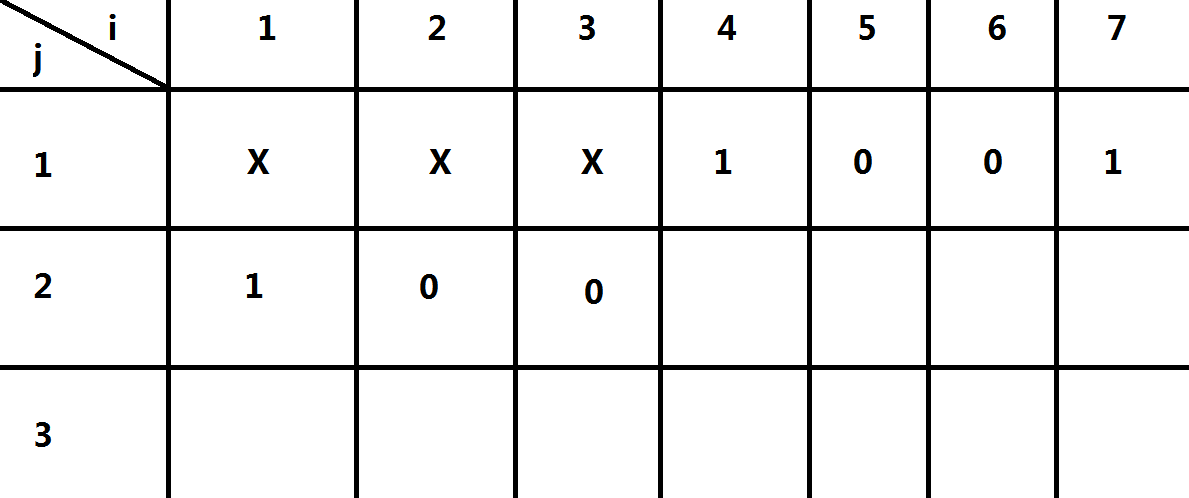
这个就是处理到 (3,2)， 就相当于假设你要看 (4,2) 的位置，那能影响它的就 (3,2) 跟 (4,1)。（后面的我们先不管）那我们就只需要关心每列最小面的值，状态个数就由 (2^{n+m}) 变成 (2^n/2^m)。
（虽然在这道题中我是竖着来的，不过是同一个道理）

然后就转移，先看你原来状态的要看的位置，如果有 (1) 就只能不选。
然后否则就是可以选可以不选，自己转移一下就可以了。
（不会转移？自己看代码去）

然后复杂度啊就是 (O(nm2^{m})) 加点 O2 就可以过掉 jzoj。

代码

#pragma GCC optimize(2)

#include<cstdio>
#include<cstring>
#define mo 100000000

using namespace std;

bool a[21][21];
int n, m, now, re;
int f[2][530001], ans;
char c;

int read() {
	re = 0;
	c = getchar();
	while (c < '0' || c > '9') c = getchar();
	while (c >= '0' && c <= '9') {
		re = (re << 3) + (re << 1) + c - '0'; 
		c = getchar();
	}
	return re;
}

int main() {
//	freopen("cowfood.in", "r", stdin);
//	freopen("cowfood.out", "w", stdout);
	
	n = read(); m = read();
	for (int i = 1; i <= n; i++)
		for (int j = 0; j < m; j++)
			a[i][j] = read();
	
	f[0][0] = 1; now = 0; 
	for (int i = 1; i <= n; i++)
		for (int j = 0; j < m; j++) {
			now ^= 1;
			for (int k = 0; k < (1 << m); k++) f[now][k] = 0;
			for (int k = 0; k < (1 << m); k++) {
				int up = (1 << j) & k, lft = (j == 0 ? 0 : (1 << (j - 1)) & k);
				if (i == 1 && up) continue;//出现非法情况
				if (j == 0 && lft) continue;
				if (up) {//只能不选
					f[now][k ^ (1 << j)] += f[now ^ 1][k];
					if (f[now][k ^ (1 << j)] > mo) f[now][k ^ (1 << j)] -= mo;
					continue;//注意这里原本是选的，要变成不选，所以要疑惑
				}
				if (lft || !a[i][j]) {//这里也是只能不选，但原本就是不选
					f[now][k] += f[now ^ 1][k];
					if (f[now][k] > mo) f[now][k] -= mo;
					continue;
				}
				//可以选也可以不选
				f[now][k] += f[now ^ 1][k];
				if (f[now][k] > mo) f[now][k] -= mo;
				f[now][k ^ (1 << j)] += f[now ^ 1][k];
				if (f[now][k ^ (1 << j)] > mo) f[now][k ^ (1 << j)] -= mo;
			}
		}
	
	for (int i = 0; i < (1 << m); i++)
		ans = (ans + f[now][i]) % mo;
	printf("%d", ans);
	
	fclose(stdin);
	fclose(stdout);
	
	return 0;
}