学习记录：二叉树

目录

• 二叉树
  • 二叉树的性质
  • 二叉树的储存
  • 二叉树的遍历
    • 广度优先遍历
    • 深度优先遍历
  • 根据遍历结果确定二叉树
    • 先序遍历+中序遍历

二叉树

二叉树的性质

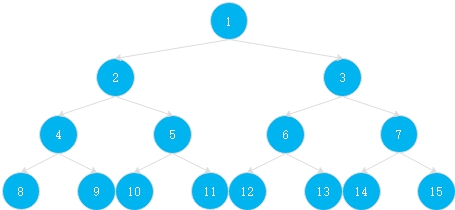
每个节点最多都有两个子节点的树称为二叉树。其性质与定义有：

• 第(i)层最多有(2^{i-1})个节点
• 满二叉树：若每一层的节点数都是满的（都为(2^{i-1})），则为满二叉树
• 完全二叉树：一棵满二叉树只在最后一层有缺失，则称为完全二叉树

而对于完全二叉树，它的子节点与父结点还有一种性质

• 对于编号为(i)的节点，其父节点为(i/2)

• 如果编号为(i)的节点有子节点，则其左节点编号为(2i)与(2i+1)

  PS：编号从1开始

二叉树的储存

一般用指针，和链表同理

struct node{
	int value;
	node *l,*r;
};

用数组也可以，而且能更为直观的表现完全二叉树中子节点与父节点的关系，但是要注意编号从1开始

二叉树的遍历

先用数组模拟来实现遍历，这里设二叉树为 int num[]={-1,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};

广度优先遍历

void BFS(int start)
{
	queue<int> q;
	q.push(start);
	cout<<num[start]<<" ";
	while (!q.empty()){
		int t1=q.front()*2,t2=q.front()*2+1;
		if (t1<16){
			q.push(t1);
			cout<<num[t1]<<" ";
		}
		if (t2<16){
			q.push(t2);
			cout<<num[t2]<<" ";
		}
		q.pop();
	}
}

深度优先遍历

深度遍历一颗二叉树共有三种方式

• 先序遍历：按父节点->左儿子->右儿子的顺序遍历
• 中序遍历：按左儿子->父节点->右儿子的顺序遍历
• 后序遍历：按左儿子->右儿子->父节点的顺序遍历

【数据结构】理解二叉树的三种遍历--前序、中序、后序 +层序（简明易懂）强烈推荐这一篇，这一篇博客写的非易懂

不难发现三种遍历其实就互相调整了一下顺序，用递归可以很简单的实现

void preorder(int root)
{
	if (root>16)
		return ;
	cout<<num[root]<<' ';
	preorder(root*2);
	preorder(root*2+1);
}
void inorder(int root)
{
	if (root>16)
		return ;
	inorder(root*2);
	cout<<num[root]<<' ';
	inorder(root*2+1);
}
void postorder(int root)
{
	if (root>16)
		return ;
	postorder(root*2);
	postorder(root*2+1);
	cout<<num[root]<<' ';
}

如果是用指针实现的，那么把退出条件改一下，root*2替换为左指针，root*2+1替换为右指针即可

根据遍历结果确定二叉树

确定二叉树的结构，需要至少两种遍历结果

• 先序遍历+中序遍历
• 中序遍历+后序遍历

如果是先序遍历+后序遍历则无法确定一棵二叉树，如图。这时先序遍历+后序遍历的结果相同

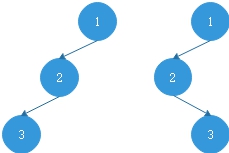
先序遍历+中序遍历

从推荐的那篇博客，不难发现中序遍历有一个特点：对于一个节点，在中序遍历的结果中，这个节点的左边的节点在二叉树中都在原节点的左边，右边同理。（因为中序遍历可以看作二叉树的投影）

这里以hdu 1710为例，这道题就是已知先序遍历+中序遍历，求后序遍历

先序遍历：1 2 4 7 3 5 8 9 6

中序遍历：4 7 2 1 8 5 9 3 6

1. 先序的第一个数是整个二叉树的根，再看中序，根据上面说的中序遍历特点可以把所有数字分成两块，472和85936，前者在1的右边，后者在1的左边
2. 先序的第二个数是前一子树的根，以此类推，4 7又可以放在2的右边
3. 递归求解，获得一棵二叉树~

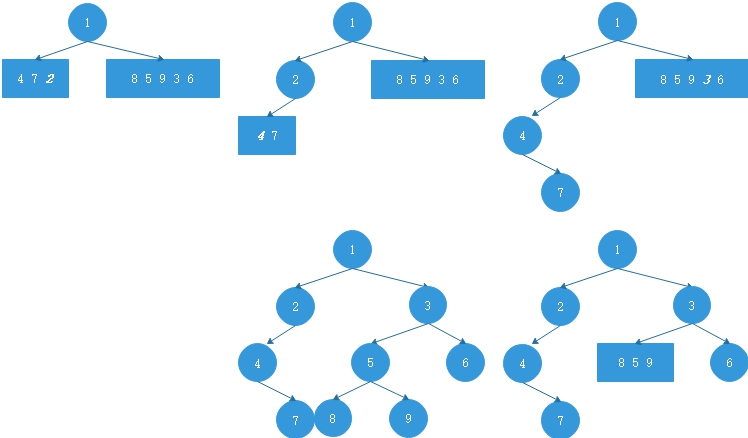
图示过程如上

hdu 1710代码如下

#include <bits/stdc++.h>
using namespace std;
const int maxn=1e3+10;
int pre[maxn],in[maxn],pos[maxn],n,pla;
void solve(int l,int r)
{
	if (l>r) return ;
	pla++;
	if (l==r){
		printf("%d ",in[l]);
		return ;
	}
	int temp=pla;
	for (int i=l;i<=r;i++){
		if (pre[temp]==in[i]){
			solve(l,i-1);
			solve(i+1,r);
			break;
		}
	}
	printf("%d",pre[temp]);
	if (temp>1)
		printf(" ");

}
int main ()
{
	while (~scanf("%d",&n)){
		for (int i=1;i<=n;i++)
			scanf("%d",&pre[i]);
		for (int i=1;i<=n;i++)
			scanf("%d",&in[i]);
		pla=0;
		solve(1,n);
		cout<<endl;
	}
	return 0;
}