算法方向分析
对于这题 (le 1000000) 的数据规模显然只允许我们用一重循环。
最长，可见这是道最值问题。
最值问题可以用贪心，DP，二分……
这道题我们用 DP 来做。
构建状态
首先，我们需要构建状态，状态的构建不是唯一的，受最长上升子序列的影响，我是这样构建的：令 (f_i) 为以 (s_i) 结尾的字符串最长匹配。
考虑 (s_i)，要想它能构成括号匹配，很显然地，它肯定不能为(或者[。
我们要找到一个 (s_k=) ( 或 [，使得在 ((k,i))这个开区间内的字符串为最长括号匹配且 ([k,i]) 这个闭区间尽可能得大。
那么什么情况能满足上面的条件呢？
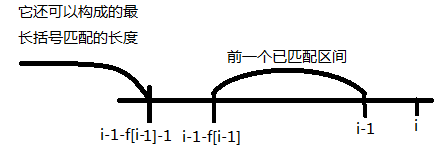
考虑每一个 (f_{i-1})，它是以 (s_{i-1}) 结尾的最长括号匹配。当 (s_i) 与 (large s_{i-1-f_{i-1}}) 匹配时，长度增加 (2)，链接起前面的最长括号匹配，如图所示。
因此公式为：
[huge f_i=f_{i-1}+2+f_{i-f_{i-1}-2}
]
如果难理解的话，不如看这个栗子 ((()[]())（每个字符记为 (s_{1,2,dots,6})），带入公式得：
[large f_9=f_8+2+f_{6}
]
对于第 (9) 个字符，它可以与它对应的括号共同对答案贡献 (2) 个。但这个区间里不一定只有一个镶嵌区间，它可能有多个。因此我们要把上一最长区间加起来。上一组区间计算时已经把上上一组区间包含在内，因此无需重复计算。
那么若 (large s_{i-1-f_{i-1}}) 与 (s_i) 不匹配怎么办？这时 (f_i) 肯定为 (0)，因为除此之外，不管选哪个字符，都没法满足它和 (s_i) 构成括号匹配。
大家自己画个图动手算一算就很明显了。
分析千万条，代码第一条，不懂的看一下代码。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int f[N];
int main() {
string s;
cin>>s;
int ans=0,id;
for(int i=1; i<s.size(); i++) {
if(s[i]=='('||s[i]=='[') {
continue;
}
if((s[i]==')'&&s[i-f[i-1]-1]=='(')||(s[i]==']'&&s[i-f[i-1]-1]=='[')) {
f[i]=f[i-1]+2+f[i-f[i-1]-2];
if(f[i]>ans) {
ans=f[i],id=i;
}
}
}
for(int i=id-ans+1; i<=id; ++i) {
printf("%c",s[i]);
}
return 0;
}
