这个人怎么一天水四篇题解
%%%chen_zhe女装大佬
如果这题没有环的话只能算是一个简单dp题,然而有了环就会出现一些非常诡异并且棘手的情况。
首先看一下这组数据,由可爱的机房友人提供。
5 5
1 4
4 2
3 5
5 3
3 4
要画出来的话,大概是这个样子:
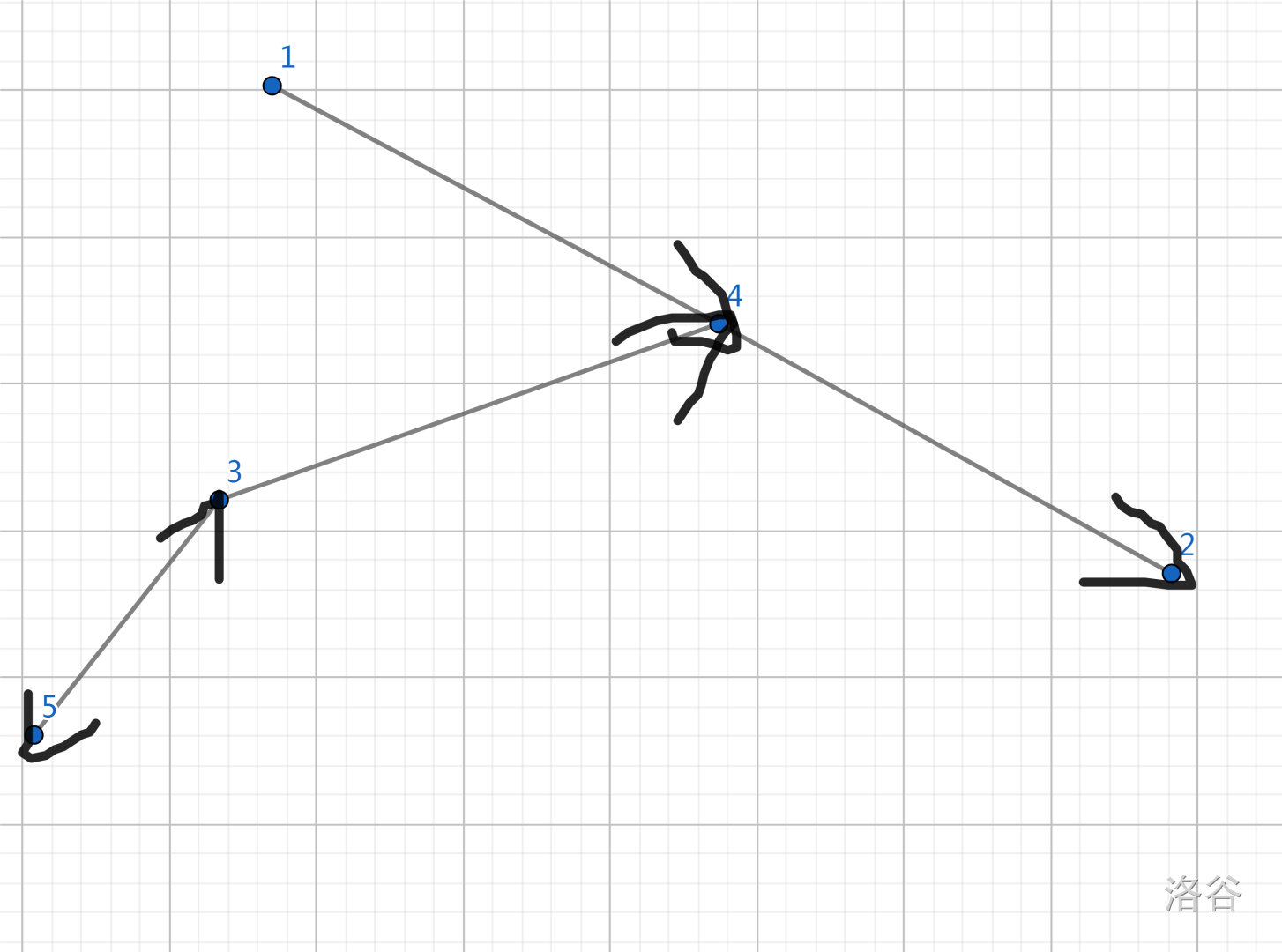
卧槽这是什么垃圾东西
总之就是,由1出发,4的入度-1,然而4的入度仍不为零,无法进行进一步的运算了。要说有环还的确是有环,不过这个环不仅没用还让我们的(dp_2)的值变成了0。
这样的毒瘤东西绝对不能要啊,但是怎么样的点才是像这样没用的点呢?我们发现,环里面的点可以到达2,但是从1根本就进不去这个环啊。
那么我们分别以1和2为起点进行一次正dfs和一次逆dfs标记能够从1能够到达的点和能够到达2的点。
必须两个都能到达才是有用的点,否则就要把这个点删掉。
然后删完就能快乐dp了。首先到达1的方法数肯定是1,然后对于每个没有前驱的点,将它的后继的方法数加上该点的方法数,删除该点和与该点相连的边。就是拓扑排序。
参考代码和其他补充如下:
#include<bits/stdc++.h>
using namespace std;
int n,m,u,v,in[10005];
long long dp[10005];
bool mk[10005][2],flag;
vector<int>dis[10005],des[10005];
queue<int>que;
void ring0(int p){
mk[p][0]=1;
for(int i=0;i<dis[p].size();i++)
if(!mk[dis[p][i]][0])
ring0(dis[p][i]);
}//标记以1为起点能够达到的点
void ring1(int p){
mk[p][1]=1;
for(int i=0;i<des[p].size();i++)
if(!mk[des[p][i]][1])
ring1(des[p][i]);
}//标记能够达到2的点
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>u>>v;
dis[u].push_back(v);
des[v].push_back(u);
in[v]++;
}
dp[1]=1;
ring0(1);
ring1(2);
for(int i=1;i<=n;i++)
if(!mk[i][1]||!mk[i][0])
for(int j=0;j<dis[i].size();j++)
in[dis[i][j]]--;//删除无用点
for(int i=1;i<=n;i++)
if(in[i]==0&&mk[i][0]&&mk[i][1])
que.push(i);//拓扑排序初始化
int top;
while(!que.empty()){
top=que.front();
que.pop();
for(int i=0;i<dis[top].size();i++){
if(in[dis[top][i]]&&mk[dis[top][i]][0]&&mk[dis[top][i]][1]){
dp[dis[top][i]]+=dp[top];//dp刷表转移
dp[dis[top][i]]%=1000000000;
in[dis[top][i]]--;
if(in[dis[top][i]]==0)
que.push(dis[top][i]);//拓扑排序过程。
}
}
}
for(int i=1;i<=n;i++)
if(in[i]&&mk[i][0]&&mk[i][1]){
cout<<"inf";
return 0;
}//如果有用的点的入度还不为0,那么在1到2的路径上存在环,输出inf
cout<<dp[2];
}
I'm Schwarzkopf Henkal.