题意:给你c,d,每次询问的bi,p=998244353,求x数组(解方程)。
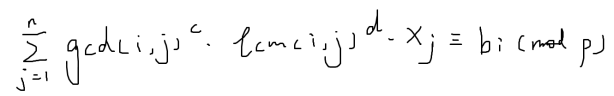
标程:
1 #include<cstdio> 2 using namespace std; 3 typedef long long ll; 4 const int mod=998244353,pmod=mod-1; 5 const int N=100005; 6 int n,c,d,q,I1[N],I2[N],b[N],a; 7 inline int ksm(int x,int y) { 8 int res=1; y=y%pmod+(y<0?pmod:0); 9 while (y) {if (y&1) res=(ll)res*x%mod; x=(ll)x*x%mod; y>>=1;} 10 return res; 11 } 12 inline void mo_inv(int *a)//筛因数反演 13 { 14 for (int i=1;i<=n;i++) 15 for (int j=2*i;j<=n;j+=i) a[j]=((ll)a[j]-a[i]+mod)%mod; 16 } 17 inline void mo_Inv(int *a)//筛倍数反演 18 { 19 for (int i=n;i>=1;i--) 20 for (int j=2*i;j<=n;j+=i) a[i]=((ll)a[i]-a[j]+mod)%mod; 21 } 22 int main() 23 { 24 scanf("%d%d%d%d",&n,&c,&d,&q); 25 for (int i=1;i<=n;i++) I1[i]=ksm(i,c-d),I2[i]=ksm(i,-d); 26 mo_inv(I1); 27 for (int i=1;i<=n;i++) I1[i]=ksm(I1[i],-1); 28 while (q--) 29 { 30 for (int i=1;i<=n;i++) scanf("%d",&b[i]),b[i]=(ll)b[i]*I2[i]%mod; 31 mo_inv(b);int fl=0; 32 for (int i=1;i<=n;i++) {if (!I1[i]&&b[i]) {fl=1;break;}b[i]=(ll)b[i]*I1[i]%mod;} 33 if (fl) {puts("-1");continue;} 34 mo_Inv(b); 35 for (int i=1;i<=n;i++) printf("%d%c",(ll)b[i]*I2[i]%mod,(i==n)?10:32); 36 } 37 return 0; 38 }
易错点:1.被一个莫名其妙的卡时卡了10发+。
y=y%pmod+(y<0?pmod:0);这样写,用mod-1代替pmod都不行,不懂。注意负幂次需要+mod-1(费马小定理证明)。
题解:莫比乌斯反演
套路是化简式子,换元,用mobius的形式代入(n=φ*1):
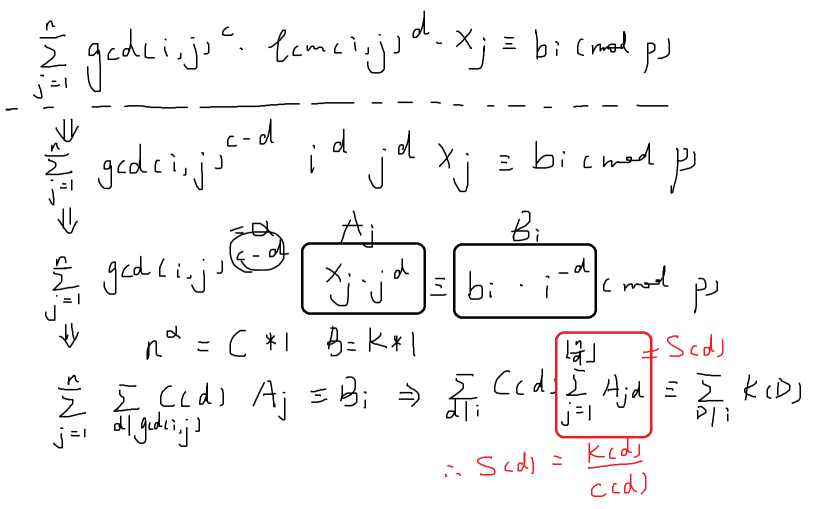
求C,就是将n^a做反演。K亦然。求出S后(注意特判无解),发现从S推回A也是一个mobius反演的形式(不同的是枚举倍数)。于是一共做三次mobius反演即可,不用筛u(没有意义,筛u一般用于求sigma_i sigma_j [(i,j)=1]=sigma_i,j sigma d|i,d|j u(d)),用欧拉筛枚举因数/倍数即可。时间复杂度O(qnlogn).